Um levantamento foi realizado para se avaliar, por município, a quantidade de obras que estão sob suspeita de irregularidade. Com base em uma amostra de municípios, foi obtida a distribuição de frequências mostrada na tabela abaixo.
![]()
Julgue a assimetria desta distribuição.
Passo 1
Podemos começar ilustrando esses dados aí num diagrama de frequências, colocando os valores de no eixo horizontal e as frequências absolutas no eixo vertical:
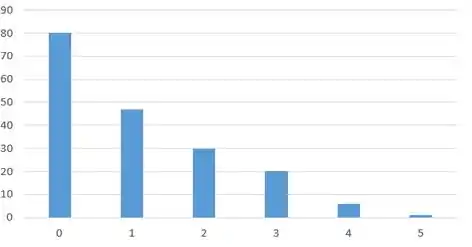
Opa! Só olhando pra esse gráfico já tá na cara que a distribuição não é simétrica. Reparou que a moda, ou seja, a maior frequência, não tá centralizada? Isso aí por si só já é uma prova.
Passo 2
Mas vamos quantificar o quão assimétrica ela é calculando o coeficiente de Pearson:
Podemos começar calculando a média amostral, que é dada por:
Onde é a frequência relativa de cada , que é dada por:
Onde é a frequência absoluta e é o número total de frequências. Para calcular basta somarmos todas as frequências dadas na tabela:
Então agora podemos calcular a média:
Agora podemos calcular o desvio padrão:
Lembrando que aqui temos esse aí dentro por que os dados tem frequência diferente de 1!
E a moda é o com maior frequência absoluta, ou seja . Agora podemos calcular o coeficiente substituindo os valores:
Opa, e quando nosso é maior que , vimos que temos uma assimetria positiva forte!
Resposta
Assimetria positiva forte