Assimetria e curtose
Produzido por Jorge Alberto NascimentoTeoria
Fala aí, você chegou no Responde Aí! E agora vamos falar um pouco sobre medidas de assimetria e curtose.
Assimetria e simetria
Dá uma olhada nessas distribuições:
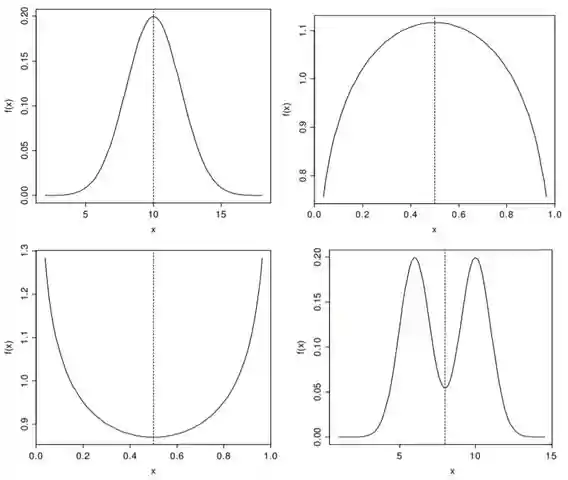
Se você notar bem, todos os gráficos da figura são espelhados em relação a uma linha vertical pontilhada. Todas esses gráficos representam distribuições simétricas, como se o gráfico fosse espelhado.
A distribuição normal, t-student e uniforme são exemplos de distribuições simétricas
Beleza! Mas e o que seria uma distribuição assimétrica? Dá uma olhada nesses gráficos:
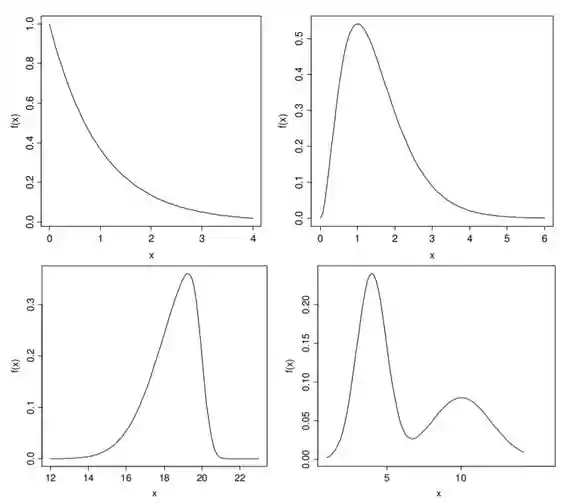
Percebeu que essas daqui não tem aspecto espelhado? O que isso significa?! Que essas distribuições são assimétricas! Vamos ver melhor as características de cada uma separadamente.
Distribuições simétricas
Agora que temos a noção gráfica do que é uma distribuição simétrica, você tem que saber que a definição matemática é:
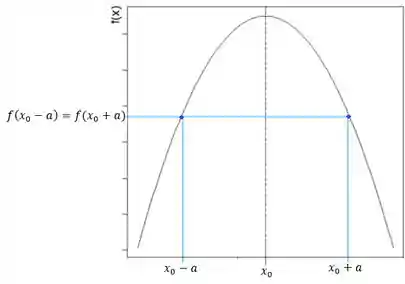
Ou seja, se
Na prática
Um detalhe importante sobre essas distribuições é a posição da mediana e da moda dos valores. A média, a mediana e a moda sempre coincidem no mesmo ponto, que é sempre o ponto central!
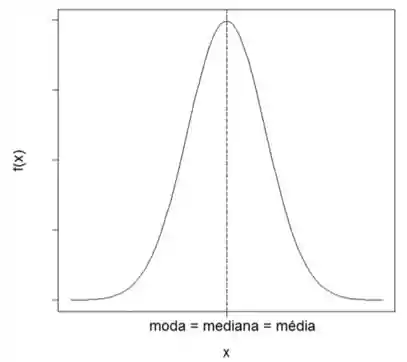
Distribuições assimétricas
Nas distribuições assimétricas, vamos ver que a média, a mediana e a moda na verdade não coincidem.
Dentre as assimétricas mais famosas na estatística podemos lembrar da distribuição Qui-Quadrado ou da Fischer-Snedecor!
Temos dois tipos de distribuições assimétricas:
- Assimétrica positiva: quando
Um detalhe legal, é que distribuições assimétricas positivas tem o lado direito mais alongado assim:
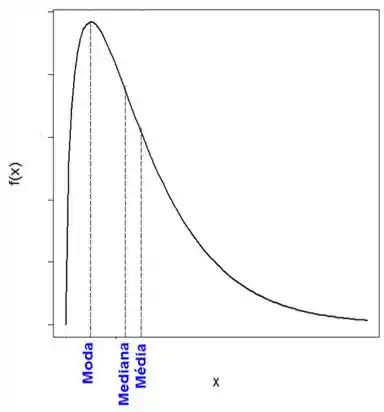
Distribuição assimétrica positiva - Assimétrica negativa: quando
Essas distribuições tem o lado esquerdo mais alongado, dessa forma:
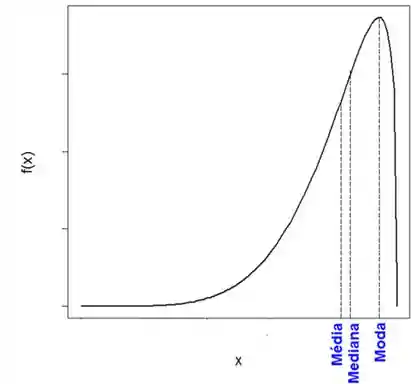
Distribuição assimétrica negativa
Coeficiente de Assimetria de Pearson
Existe uma forma matemática de determinar a “intensidade” da assimetria, é o coeficiente de assimetria de Pearson, dado pela fórmula
Onde:
Para analisar o coeficiente de assimetria fazemos assim:
- Se
então a curva é simétrica - Se
então a curva é assimétrica positiva fraca - Se
então a curva é assimétrica positiva forte - Se
então a curva assimétrica negativa fraca - Se
então a curva é assimétrica negativa forte
Curtose
A curtose é uma medida que diz se uma distribuição é achatada ou não. Pra entender melhor dá uma olhada nessa figura:
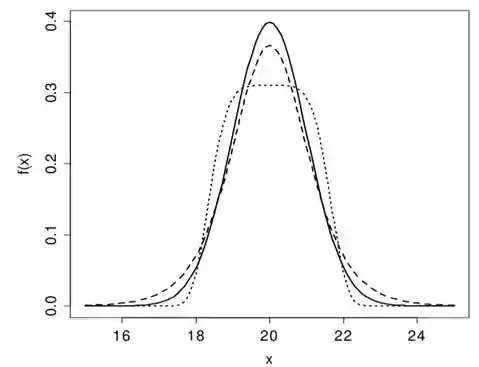
Temos três curvas aí nessa figura, todas simétricas mas diferentes entre si, correto? A diferença entre elas é o justamente, o achatamento. E é exatamente isso que a curtose vai descrever, o quão achatada é uma distribuição!
Para calcular a curtose usamos:
Tipos de curtose
Depois de calcular a curtose é necessário interpretar o valor de
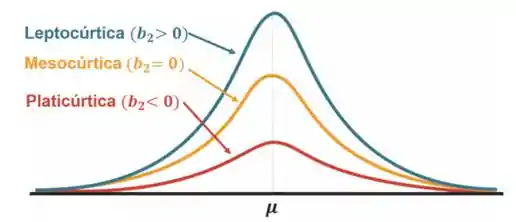
- Quanto maior for o valor da curtose, menos achatada é a curva!
- Se
chamamos de curva leptocúrtica - Se
chamamos de curva mesocúrtica (Por exemplo, a distribuição normal) - Se
chamamos de curva platicúrtica
Exemplo
11 idosos foram entrevistados. Foram listadas as idades em que cada um deles se aposentou:
a) Determine se é uma distribuição simétrica
b) Calcule a curtose
Passo 1: Primeiro vamos precisar calcular a média, mediana, moda e desvio padrão
Então vamos colocar a distribuição em ordem:
Vemos que a mediana é:
E observamos que a moda é:
A média é:
E o desvio padrão é:
Passo 2: Agora vamos calcular se a distribuição é ou não é simétrica usando Coeficiente de Assimetria de Pearson
Ou seja,
Passo 3: Agora vamos verificar a curtose:
Então essa é uma curva do tipo platicúrtica.
Videoaula
Quer aprender ainda mais? Então se liga nessa super videoaula sobre o tema:
E agora vamos praticar fazendo uns exercícios de fixação aqui em baixo 👇
Curtose
Exemplo
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
ASSEMBLEIA LEGISLATIVA/CE 2011 - CESPE - ANALISTA LEGISLATIVO - ESTATÍSTICA
Um levantamento foi realizado para se avaliar, por município, a quantidade de obras que estão sob suspeita de irregularidade. Com base em uma amostra de municípios, foi obtida a distribuição de frequências mostrada na tabela abaixo.
![]()
Julgue a assimetria desta distribuição.
Passo 1
Podemos começar ilustrando esses dados aí num diagrama de frequências, colocando os valores de no eixo horizontal e as frequências absolutas no eixo vertical:
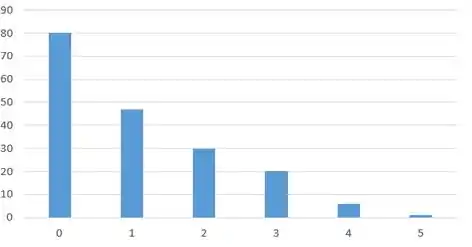
Opa! Só olhando pra esse gráfico já tá na cara que a distribuição não é simétrica. Reparou que a moda, ou seja, a maior frequência, não tá centralizada? Isso aí por si só já é uma prova.
Passo 2
Mas vamos quantificar o quão assimétrica ela é calculando o coeficiente de Pearson:
Podemos começar calculando a média amostral, que é dada por:
Onde é a frequência relativa de cada , que é dada por:
Onde é a frequência absoluta e é o número total de frequências. Para calcular basta somarmos todas as frequências dadas na tabela:
Então agora podemos calcular a média:
Agora podemos calcular o desvio padrão:
Lembrando que aqui temos esse aí dentro por que os dados tem frequência diferente de 1!
E a moda é o com maior frequência absoluta, ou seja . Agora podemos calcular o coeficiente substituindo os valores:
Opa, e quando nosso é maior que , vimos que temos uma assimetria positiva forte!
Resposta
Assimetria positiva forte
Exercício Resolvido #2
P1 PUC-RIO 2018.1, 1b
Defina o que é uma distribuição platicúrtica. Mostre através de um esboço a relação entre os três tipos (Mesocúrtica, leptocúrtica e platicúrtica).
Passo 1
Antes de definir essas distribuições, precisamos lembrar o que é curtose. A curtose () é uma medida que caracteriza o quanto uma curva de função de probabilidade é achatada.
A curva da distribuição normal é usada como padrão para uma curva mesocúrtica, ou seja, com curtose igual a zero.
A distribuição leptocúrtica é aquela que é mais alta e concentrada que a distribuição normal, carinhosamente chamada também de distribuição com “caudas pesadas”. Tem curtose maior que zero.
E finalmente, vamos definir a distribuição platicúrtica. Ela é a distribuição que tem curva mais achatada que a normal, um exemplo é a distribuição T de Student! Tem curtose menor que zero.
Passo 2
Um gráfico relacionamento as três seria tipo esse aqui:
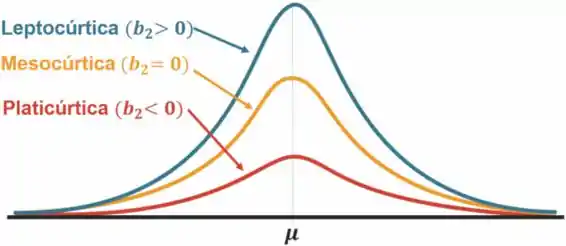
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
SEEDUC/AM 2011 - CESPE - ESTATÍSTICO
Considerando as densidades de probabilidade ilustradas na figura acima, julgue os itens que se seguem a respeito dos momentos dessas distribuições.
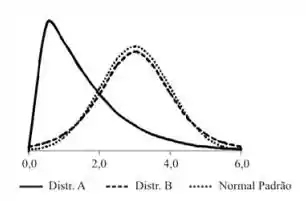
Julgue a curtose da distribuição B e a assimetria da distribuição A.
Passo 1
Se olharmos direitinho vemos que a distruibução B está abaixo da distribuição da Normal Padrão, o que quer dizer que ela está mais achatada que a Normal! Quando temos uma distribuição mais achatada que a Normal, dizemos que essa distribuição é platicúrtica e tem curtose negativa.
E quando a distribuição A, vemos que ela é assimétrica e está deslocada para a esquerda, e esse tipo de assimetria é classificada como assimetria positiva (ou à direita! – porque a cauda é mais longa na direita.)
Resposta
Distribuição A: assimétria positiva
Distribuição B: Platicúrtica