Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelos mecânicos

Ver Teoria
Exercício 61234578

Enunciado

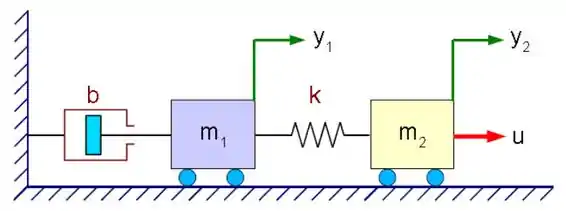
Encontre as funções de transferência Y 1 s U s e Y 2 s U s do sistema abaixo:

Passo 1

Vamos escrever a equação de equilíbrio de forças para cada um dos corpos.

Para o bloco 1:

m 1 d 2 y 1 d t 2 = - b d y 1 d t - k y 1 - y 2

O primeiro sofre influência da força de amortecimento e da força da mola.

Para o bloco 2:

m 2 d 2 y 2 d t 2 = u ( t ) - k y 2 - y 1

O segundo bloco sente o efeito apenas da força da mola e da força u ( t )

Vamos rearranjar essas expressões para ficar melhor para a gente trabalhar:

m 1 d 2 y 1 d t 2 + b d y 1 d t + k y 1 = k y 2

m 2 d 2 y 2 d t 2 + k y 2 = u t + k y 1

Passo 2

As EDOs já estão no jeito. Vamos aplicar Laplace nelas então:

m 1 s 2 Y 1 s + b s Y 1 s + k Y 1 s = k Y 2 s                       ( 1 )

m 2 s 2 Y 2 s + k Y 2 s = U s + k Y 1 S                             ( 2 )

Só lembrando: se você não está se lembrando como fazer esse passo, seria legal dar uma revisa em transformadas de Laplace. Esse passo é fundamental e precisa estar na ponta da língua hein.

Passo 3

Vamos isolar Y 1 ( s ) em ( 1 ) e substituir em ( 2 ) :

Y 1 s = k Y 2 s m 1 s 2 + b s + k         ( 3 )

Substituindo:

m 2 s 2 Y 2 s + k Y 2 s = U s + k 2 Y 2 s m 1 s 2 + b s + k  

Rearranjando:

m 2 s 2 + k - k 2 m 1 s 2 + b s + k Y 2 s = U ( s )

m 2 s 2 + k m 1 s 2 + b s + k - k 2 Y 2 s = m 1 s 2 + b s + k U ( s )

Por fim:

Y 2 s U s = m 1 s 2 + b s + k m 2 s 2 + k m 1 s 2 + b s + k - k 2             ( 4 )

Substituindo 4 em ( 3 ) :

Y 1 s = k U s m 2 s 2 + k m 1 s 2 + b s + k - k 2

Y 1 s U s = k m 2 s 2 + k m 1 s 2 + b s + k - k 2

Resposta

Y 1 s U s = k m 2 s 2 + k m 1 s 2 + b s + k - k 2

Y 2 s U s = m 1 s 2 + b s + k m 2 s 2 + k m 1 s 2 + b s + k - k 2