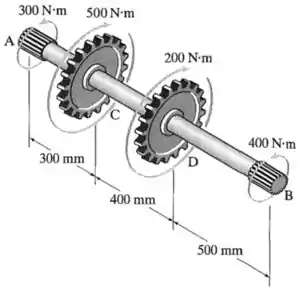
O eixo maciço de de diâmetro é usado para transmitir os torques aplicados às engrenagens. Determine a tensão de cisalhamento máxima absoluta no eixo.
Passo 1
O que está acontecendo?
O eixo maciço tem um diâmetro (e, consequentemente, um raio ) e está submetido à diferentes torques externos nos pontos , , e .
Sendo assim, ele vai resistir à diferentes torques internos nos trechos , e .
E o que é que o exercício quer?
Ele quer saber qual é a tensão de cisalhamento máxima absoluta no eixo.
Essa tensão máxima absoluta vai ocorrer no trecho do eixo que estiver resistindo ao maior torque interno .
Então o nosso primeiro passo vai ser identificar qual é o maior torque interno no eixo.
Feito isso, vamos poder usar a fórmula da torção para calcular a tensão de cisalhamento máxima absoluta no eixo:
Passo 2
Então vamos começar o exercício identificando qual é o maior torque interno no eixo.
E como é que a gente faz isso? 🤔
Do mesmo jeito que a gente encontrava a maior força interna normal em um eixo: fazendo um DCL (Diagrama de Corpo Livre) e uma análise dos esforços internos da peça.
Então vamos lá!
Primeiro, para fazer o DCL, usamos a regra da mão direita para representar os torques na forma de setas duplas:

Com isso, o nosso DCL fica assim:

Show! 😎
Agora, para encontrar os torques internos em cada trecho do eixo, fazemos uma análise dos esforços internos nas seções entre e , e & e :
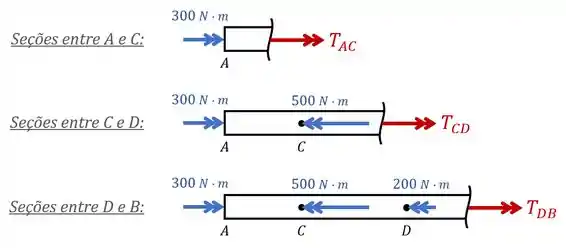
Nessa análise, desenhamos os torques internos em vermelho “saindo” da peça pois essa é a nossa convenção.
Caso os seus professores utilizem a convenção contrária (a de que os torques internos são positivos quando “entram” nas peças), você deve desenhar os torques internos entrando.
Aplicando o equilíbrio de torques para cada caso, vamos ter que:
Em seguida, isolando os torques em cada uma dessas equações, encontramos que:
Com isso, percebemos que o torque de maior intensidade no nosso eixo é o torque que atua nas seções entre e ! 👌
Além disso, caso seja necessário, podemos representar o resultado que encontramos em um diagrama do momento torsor para o nosso eixo:
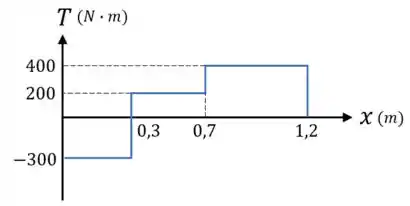
Dica do Expert:
Alguns professores permitem que você faça todo esse passo de cabeça e só diga “O maior torque acontece nas seções entre e , onde ”.
Por outro lados, existem outros professores, mais rígidos, que cobram que você faça tudo (DCL, análise dos esforços internos & diagrama do momento torsor) no papel. 😕
Passo 3
Agora que já identificamos o torque máximo na peça, podemos calcular a tensão de cisalhamento máxima absoluta.
Para tanto, vamos usar a fórmula da torção:
Por termos um eixo maciço, o momento polar de inércia vai ser dado por .
Além disso, como queremos saber a tensão máxima absoluta, devemos usar o torque máximo na peça, ou seja, .
Dessa forma, temos que:
Simplificando tudo, isso fica assim:
Por fim, substituindo os valores:
- ;
- & ,
Encontramos que:
E, usando que é o mesmo que , definimos a nossa resposta final: