Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio de Stevin e Manômetros

Ver Teoria
Exercício 3124567891011

Enunciado

Encontre a densidade do fluido A na figura abaixo.

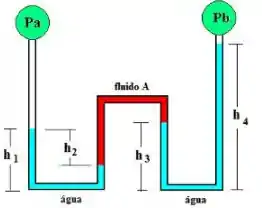
Passo 1

Uma questão típica de manômetros. Já resolvemos muitas questões usando o método de escolher dois pontos no mesmo fluido e mesma altura para podermos igualar as pressões.

Bem, essa é uma questão que resolver por este método daria muito trabalho, teríamos que pegar vários pontos, ir igualando as pressões.

Por isso, nessa vamos utilizar o método de montar apenas uma equação de pressão para todo o sistema.

Como vimos na teoria, vamos começar de um lado e assumir que tudo que está para baixo é positivo e tudo que percorrermos subindo será negativo e no final tudo isso será igual a pressão no outro extremo.

Mas, para utilizarmos esse método temos que ter todas as distâncias mapeadas. Então faremos isso primeiro. Sabemos as alturas: h 1 ; h 2 ; h 3   e   h 4 , porém não sabemos o valor de x ; y ; z .

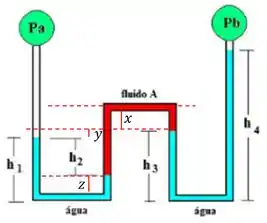
Bem, x não tem como descobrirmos mesmo, mas as outras duas medidas conseguimos descobrir. Bem, z é a diferença entre h 1 e h 2 , assim:

z = h 1 - h 2

E y é:

y = h 3 - h 2 - z

y = h 3 - h 1

Passo 2

Beleza, agora que já descobrimos as alturas. Vamos começar a montar a equação de pressão.

Iremos começar do lado esquerdo partindo de P a . E iremos percorrer o manômetro. As colunas de fluido que percorremos descendo serão positiva e as que percorrermos subindo serão negativas. Borá-la? Selecionei de laranja todos os pedaços que entraram na nossa equação:

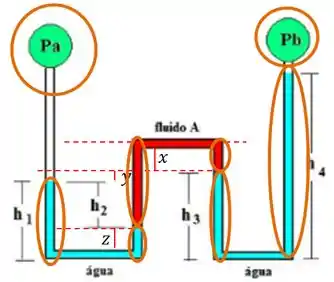
Assim, a equação fica da seguinte forma:

P a + ρ á g u a . g . h 1 - ρ á g u a . g . h 1 - h 2 - ρ A . g . h 2 + h 3 - h 1 + x + ρ A . g . x + ρ á g u a . g . h 3 - ρ á g u a . g . h 4 = P b

Vamos juntar tudo que tem ρ A . g e faremos o mesmo para tudo que tem ρ á g u a . g

P a + ρ á g u a . g . ( h 1 - h 1 - h 2 + h 3 - h 4 )   - ρ A . g . h 2 + h 3 - h 1 + x - x = P b

Ufaaaaa, aquele x que não tínhamos ideia de quanto ia valer sumiu o/.

Beleza, agora podemos isolar o termo que tem ρ A .

ρ A . g . h 2 + h 3 - h 1 = P a - P b + ρ á g u a . g . ( h 2 + h 3 - h 4 )  

Agora, encontramos o valor da densidade do fluido A .

ρ A = P a - P b + ρ á g u a . g . h 2 + h 3 - h 4 g h 2 + h 3 - h 1

Resposta

ρ A = P a - P b + ρ á g u a . g . h 2 + h 3 - h 4 g h 2 + h 3 - h 1

Exercícios de Livros Relacionados

Na Figura P2.11, o medidor de pressão manométrica A indica 1,5 kPa (manométrica). Os fluidos estão a 20°C. Determine as elevações z , em metros, dos níveis dos líquidos nos tubos piezométricos abertos
O tubo em V simétrico na Figura P2.14 contém água estática e ar a 20 °C. Qual é a pressão do ar na parte fechada no ponto B?
O tubo em U abaixo tem diâmetro interno de 1 cm e contém mercúrio como mostra a figura. Se colocarmos 20 cm³ de água no ramo direito do tubo, qual será a altura da superfície livre em cada ramo após o
O medidor de combustível de um tanque de gasolina de um carro fornece uma indicação proporcional à pressão manométrica do fundo do tanque, como mostra a figura abaixo. Se o tanque tiver 30 cm de profu
Na figura abaixo ambos os fluidos estão a 20°C. Se os efeitos da tensão superficial forem desprezíveis, qual a massa específica do óleo, em kg/m³?