Box Plot
Teoria
Identificação de Discrepâncias
Muitas vezes, quando alguém coleta um conjunto de dados de alguma coisa, alguns valores podem ser coletados de forma errada e podem ficar muito distantes dos outros.
Imagina que você coletou dados da idade dos alunos da sua turma de cálculo 3:
Opa! Esse tá meio estranho ali, você não acha? Provavelmente ouve algum erro na hora de coletar esses dados, ou até mesmo um erro de digitação, e esse carinha acabou aparecendo ali.
Nesse exemplo que eu te dei ficava fácil encontrar quem era o valor discrepante, porque você tinha um número pequeno de dados, de fácil visualização.
É interessante a gente ter algum critério pra poder identificar esses valores muito discrepantes, também conhecidos como outliers, principalmente em casos que tivermos muitos dados.
É isso que a gente vai aprender agora!
Um critério muito usado é apontar como discrepantes os valores fora do intervalo .
Lembrando que é a média amostral dos seus dados, e é o desvio padrão.
Além desse, existe um outro que você provavelmente nunca ouviu falar.
Esse segundo critério, é apontar como discrepantes todos os valores abaixo da Cerca Inferior ou acima da Cerca Superior. Vou te apresentar quem são esses caras:
Só lembrando que é o 1º quartil dos nossos dados, é o nosso 3º quartil, e é a distância interquartil.
Vamos ver um exemplo? Vem comigo!
Vamos supor que foram medidas a carga de ruptura de 30 cabos de aço diferentes, em , resultando nos valores abaixo:
Vamos utilizar o segundo critério, ok?
Já calculei os quartis pra você:
Com isso, calculando as cercas:
Logo, qualquer valor menor que e maior que podemos apontar como outliers, ou discrepantes!
Olhando para nossos dados, concluímos que nenhum dos valores de ruptura é discrepante.
BOX plot
Cara, você não aprendeu sobre quartis e distância interquartil a toa! Essas coisas servem pra muitas coisas, e vou te mostrar mais uma utilidade disso agora.
Box plot é um gráfico onde você representa a variação dos seus dados por meio dos quartis.
Vamos pra um passo a passo pra construir o nosso Box plot, utilzando o exemplo das cargas de ruptura.
Passo1) Traçar um eixo vertical pra representar os valores observados pras rupturas, em ordem crescente.
Passo2) Agora você vai desenhar um retângulo da seguinte forma: a base inferior é o valor do primeiro quartil :
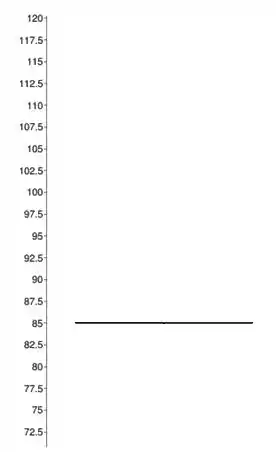
A base superior vai ser o :
Além disso, dentro do retângulo vamos representar com um traço o valor da mediana :
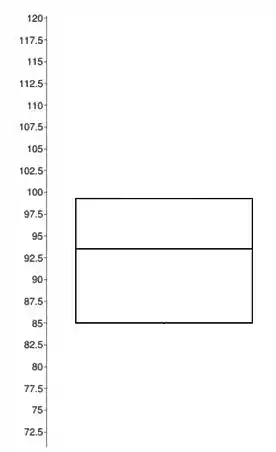
Passo3) Traçar uma uma reta vertical do meio da base superior até o maior valor observado e não discrepante.
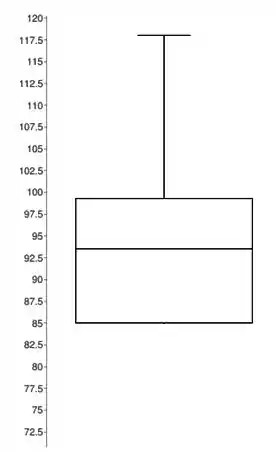
Depois disso, fazer o mesmo do meio da base inferior até o menor valor observado e não discrepante.
No fim, vamos ficar com isso aqui:
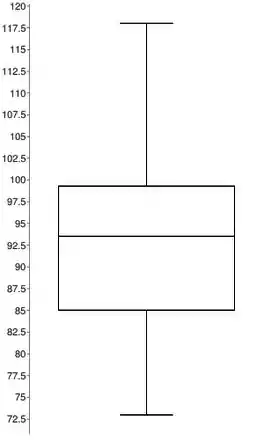
Observações IMPORTANTES:
- Erro muito comum é marcar as cercas ao invés de marcar o menor e o maior valores observados e não discrepantes.
- Os valores discrepantes, ou outliers, podem ou não ser representados no Box plot com um ponto.
- O eixo horizontal não significa nada.
Cara, essa parte da matéria tem 2 coisas que eu quero ressaltar, porque se você errar, vou ficar muito bolado. NÃO esqueça de colocar os valores em ordem crescente quando for calcular quartil; e, no Box plot, os tracinhos em cima e embaixo são o maior e o menor valores não discrepantes.
Promete pra mim que você vai fazer exercícios agora? A gente se vê por lá então!
BOX plot
Exercícios Resolvidos
Exercício Resolvido #1
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 211.
A tabela de dados brutos a seguir reporta o número de linhas telefônicas por mil habitantes em cada estado do Brasil, em 2001.
- Determine os seus quartis;
- Construa o seu Box plot;
- Há pontos discrepantes entre essas observações? Quais?
Passo 1
(a)
Primeiro passo - colocar em ordem crescente!
Passo 2
Podemos determinar os quartis:
Passo 3
(b) Pra construir o Box plot, primeiro temos que definir nossas cercas.
Passo 4
Agora é desenhar o Box plot, lembrando que o maior valor não discrepante será 362,8 e o menor valor não discrepante será 86,1. São eles que determinam aqueles tracinhos, não são as cercas, não esqueça isso.
Conseguiu entender namoral o Box plot? Meu talento no paint ainda tá em desenvolvimento haha...
Passo 5
(c)
Sim, existem pontos discrepantes. Qual seria ele?
O do D. Federal – 456,8. Porque está além da cerca superior.
Resposta
Exercício Resolvido #2
João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 281.
A tabela a seguir contém o número de domicílios rústicos em alguns municípios do Estado do Rio de Janeiro no ano 2000.
- Determine os quartis;
- Obtenha um gráfico Box plot para esses dados;
- Seria o gráfico ramo-folha adequado para representar estes dados? Por quê?
Passo 1
(a)
Pra calcular quartil, qual o primeiro passo? Colocar em ordem crescente!
Calcular os quartis:
Passo 2
(b)
Pra montar o Box plot precisamos calcular as cercas, precisamos primeiro do .
Com isso a gente percebe que o menor valor não discrepante é o próprio 51 e o maior valor não discrepante é o 914, eles que serão o limite do Box plot.
Passo 3
Agora é só desenhar o Box plot.
Você pode notar que existem alguns pontos discrepantes, por estarem além da cerca superior. Outro detalhe, é que se você caísse no erro de colocar como limite as cercas, a sua cerca inferior deu negativa, e muuuito além do menor valor, ou seja, seu Box plot ficaria muito diferente.
Passo 4
(c)
Não, o ramo-folha não seria uma boa opção porque os valores são muito discrepantes, note que o menor deles é 51 e o maior 1839.
Resposta
Exercício Resolvido #3
UFRJ, ProbEst, P2/2014.1, 1
A tabela abaixo apresenta o número de gols sofridos pela seleção brasileira de futebol em cada uma das edições da copa do mundo.
- Calcule os quartis e construa um box-plot. Existe algum valor que pode ser considerado discrepante?
Passo 1
(b)
Temos que calcular primeiro os quartis, pra isso, colocar em ordem crescente os valores. Não pode esquecer isso, senão já era.
Em ordem crecente os gols ficam:
A mediana que é o quartil é o valor do meio, como são 19 valores:
A posição do é . Então será:
A posição do é . Então será:
Passo 2
Pra construir um Box plot, temos que primeiro calcular as cercas pra ver quais valores serão discrepantes.
Já podemos ver que existe um valor que será considerado discrepante, porque está acima da cerca superior, que é o 11 da copa de 1938.
Passo 3
Agora é só desenhar o Box plot.
Resposta
Exercício Resolvido #4
Lista de exercícios 2 – Estatística Descritiva 2012.1 – IME, USP
Compare e indique as diferenças existentes entre as distribuições das variáveis notas dos cursos de Direito, Política e Estatística, utilizando o “boxplot” e as medidas calculadas em:
Por que em Direito o gráfico é uma reta? Quem tem maior variabilidade e o por qual razão? Porque a linha da mediana em Política não está centralizada? Existe algum dado discrepante?
Passo 1
Primeira coisa que percebemos é que em Direito só temos a reta da média do Box-Plot, ou seja, em Direito a nota é constante: todos alunos tiraram a mesma nota.
A nota em Política possui maior variabilidade porque a caixa do Box-Plot é maior, isso quer dizer que nosso desvio padrão é maior! O tamanho da caixa está relacionado ao desvio padrão.
A mediana em Política está mais próxima do primeiro quartil (linha inferior do retângulo) que do terceiro (linha superior do retângulo), mas como isso é possível? A quantidade de dados entre a mediana e os quartis deve ser a mesma, mas os valores desses dados não. Essa assimetria quer dizer que os valores do primeiro quartil até a mediana são mais próximos do que os valores entre a mediana e o terceiro quartil.
Pode-se observar a presença de um valor extremo (discrepante) na variável Nota em Estatística (alguém teve nota 2).
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Hoaglin, Mosteller e Tukey, 1983, apud Morettin & Bussab, Estatística Básica.
Considere novamente os dados sobre a dureza do alumínio.
Construa o Box-Plot dos dados.
Passo 1
Primeiro colocamos esses dados em ordem:
A mediana é o valor central, como temos dados, a mediana vai ser a média entre a posição e , que é:
O primeiro quartil vai estar na posição:
Fazendo a média ponderada entre os valores de posição e :
Agora o terceiro quartil:
Fazendo a média ponderada entre os valores de posição e 23:
Então o é:
Passo 2
Calculando as cercas:
Olhando nos dados, o menor valor que ainda está dentro da cerca é e não há valores discrepantes para baixo.
O maior valor que ainda está dentro da cerca é e não há valores discrepantes para cima.
Nosso gráfico fica assim então:
Resposta
