Exercícios de Box Plot - Lista de Exercícios Resolvida
Questão 1
Compare e indique as diferenças existentes entre as distribuições das variáveis notas dos cursos de Direito, Política e Estatística, utilizando o “boxplot” e as medidas calculadas em:
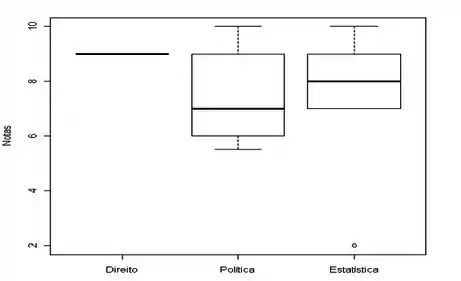
Por que em Direito o gráfico é uma reta? Quem tem maior variabilidade e o por qual razão? Porque a linha da mediana em Política não está centralizada? Existe algum dado discrepante?
Ver solução completaQuestão 2
A tabela de dados brutos a seguir reporta o número de linhas telefônicas por mil habitantes em cada estado do Brasil, em 2001.
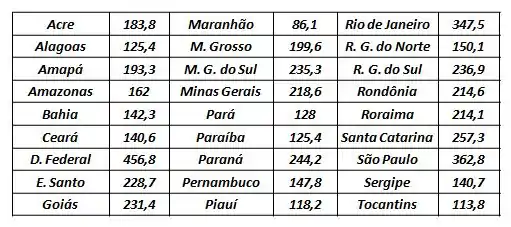
- Determine os seus quartis;
- Construa o seu Box plot;
- Há pontos discrepantes entre essas observações? Quais?
Questão 3
Considere novamente os dados sobre a dureza do alumínio.
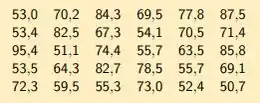
Construa o Box-Plot dos dados.
Ver solução completaQuestão 4
A tabela a seguir contém o número de domicílios rústicos em alguns municípios do Estado do Rio de Janeiro no ano 2000.
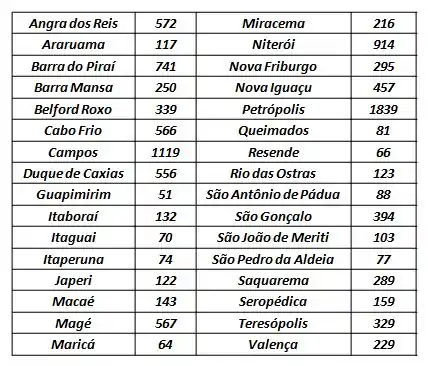
- Determine os quartis;
- Obtenha um gráfico Box plot para esses dados;
- Seria o gráfico ramo-folha adequado para representar estes dados? Por quê?
Questão 5
A tabela abaixo apresenta o número de gols sofridos pela seleção brasileira de futebol em cada uma das edições da copa do mundo.
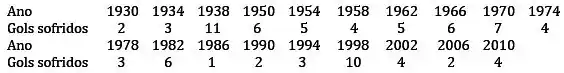
- Calcule os quartis e construa um box-plot. Existe algum valor que pode ser considerado discrepante?
Questão 6
Os dados da tabela abaixo representam o número de acidentes relacionados a uma empresa com dez construções em andamento durante os anos de 2016 e 2017.

(a) Calcule o número médio de acidentes e o desvio padrão do número de acidentes para cada ano.
(b) Calcule os quartis do número de acidentes e construa um box-plot dos dados para cada ano. Os dois box-plots devem aparecer juntos na mesma figura, ou seja, utilize a mesma escala de forma que os gráficos fiquem comparáveis. Existe(m) valor(es) discrepante(s)?
(c) Calcule o coeficiente de correlação.
Ver solução completaQuestão 7
Considere uma amostra de tempos de falha de um componente elétrico (meses) que tenha gerado o seguinte boxplot:
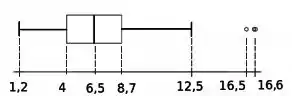
- Qual conjunto contém a maior quantidade de elementos da amostra referente aos tempos de falha: ou ? Justifique.
- Pressupondo que os quartis não serão afetados pela inclusão da nova observação, um tempo de falha de meses seria considerado um outlier de acordo com o boxplot? Justifique.
Questão 8
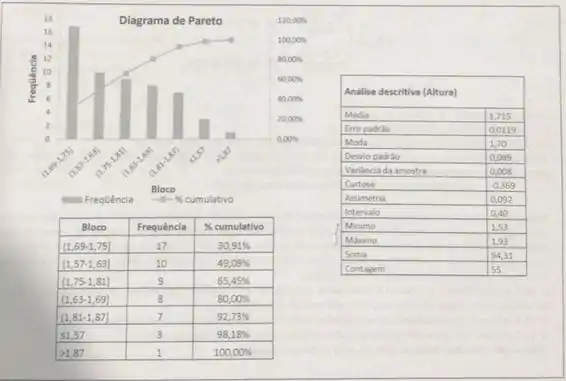
As tabelas na parte inferior correspondem às alturas dos alunos matriculados na disciplina PROBEST-2013-2, turma 3VB. Usando os dados apresentados, pede-se:
- Através da análise descritiva e do diagrama de Pareto, construir o Boxplot determinando se há valores discrepantes.
Questão 9
Construa um Boxplot determinando se há valores discrepantes no seguinte conjunto de dados vindo de uma amostra coletada em campo. Plotar todos os valores conforme a aula-1.

Questão 10
Para estimar a magnitude da aceleração da gravidade G na superfície da Terra, realizou-se o seguinte experimento. Lançou-se uma bolinha de gude a partir do repouso 146 vezes a várias alturas diferentes com relação ao solo, anotando-se cada tempo ti , i ∈ {1, 2, . . . , 146} que a bolinha levou para tocar o chão. A partir do conjunto de observações dos pares altura e tempo até a bolinha atingir o solo, obteve-se uma amostra de medições para a aceleração da gravidade, calculadas em função dos valores de ti e medidos. A figura abaixo mostra o boxplot horizontal feito a partir das medições obtidas para G no experimento.
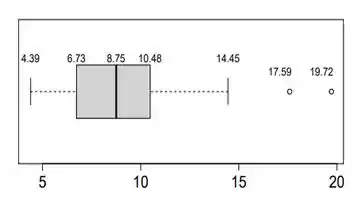
(a) Obtenha uma estimativa pontual para G com base no boxplot. Justifique.
(b) Dentre todas as medições obtidas na amostra, quantas se encontram entre e ? Justifique.
(c) Forneça as cercas do boxplot e, com elas, obtenha uma regra que permita classificar uma medição futura de G por esse experimento como outlier. A estimativa 14,56 seria considerada um outlier segundo essa regra? Por que?
Ver solução completaQuestão 11
Os quadros abaixo correspondem as alturas dos alunos matriculados na disciplina PROBEST-2012-2. Construa o boxplot determinando se há valores discrepantes no conjunto de dados apresentados. Detalhe todos os cálculos e esboce o gráfico com seus respectivos valores conforme a aula-1.
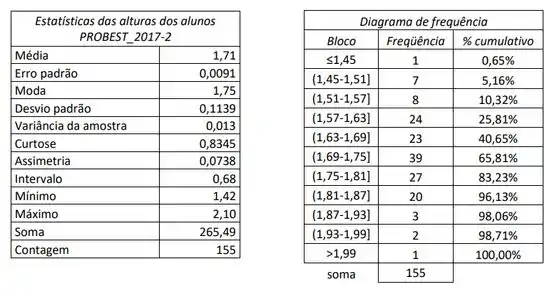
Questão 12
Cinco pessoas estão almoçando juntas. Os nomes dessas pessoas, ordenando-se em termos de idade (do mais novo pro mais velho), são: Paulo, Andrea, Jorge, Daniela e Vitor. Com base em suas idades, foram calculadas as seguintes medidas: Média , Mediana , Distância Interquartil , Amplitude (todas elas expressas em anos) e Variância anos².
- Quais são as idades de cada um deles?
- Alguma dessas cinco observações pode ser considerada discrepante, pelo critério para identificação de outliers que se baseia nos quartis da variável? Qual?
Obs.: Amplitude (Maior valor) (Menor valor).
Ver solução completaQuestão 13
Espécimes machos de aranhas do gênero Tidarren amputam voluntariamente um de seus pedipaldos (direito ou esquerdo) logo antes de atingir a maturidade sexual. Especula-se que a amputação contribui para o aumento da velocidade, o que favoreceria a procura de fêmeas. A velocidade de 9 aranhas (em cm/s) foi medida antes e depois da amputação voluntária.

- Calcule os quartis das medidas de velocidade antes e depois da amputação voluntária
- Construa dois box-plots na mesma escala para a velocidade antes e depois da amputação voluntária. Comente sobre a diferença observada. Hã valores discrepantes?
Questão 14
Construa o Boxplot determinando se valores discrepantes no seguinte conjunto de dados vindo de uma amostra coletada em campo. Plotar todos os valores conforme a aula-1.
Dados:

Questão 15
A tabela abaixo apresenta o número de gols sofridos pela seleção brasileira de futebol em cada uma das edições da copa do mundo.
Ano 1930 1934 1938 1950 1954 1958 1962 1966 1970 1974
Gols sofridos 2 3 11 6 5 4 5 6 7 4
Ano 1978 1982 1986 1990 1994 1998 2002 2006 2010
Gols sofridos 3 6 1 2 3 10 4 2 4
(b) Calcule os quartis e construa um box-plot. Existe algum valor que pode ser considerado discrepante?
Ver solução completaQuestão 16
As tabelas na parte inferior correspondem às notas G1 dos alunos matriculados na disciplina PROBEST-2013-2 turma 3VB. Usando os dados apresentados, construa o BoxPlot determinando se há valores discrepantes no conjunto de dados apresentados. Detalhar todos os cálculos e plotar todos os valores conforme a aula-1.
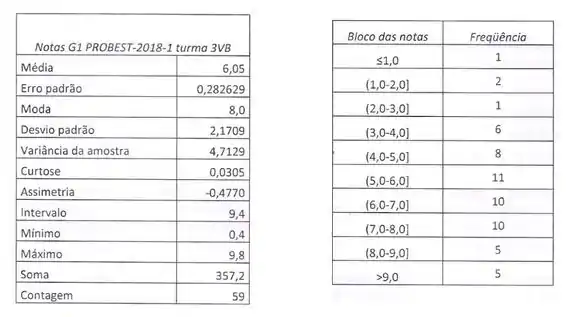
Questão 17
Os dados abaixo correspondem a notas de uma turma de Probest com 30 alunos:
Onde:
(c) Construa um desenho esquemático (boxplot).
Ver solução completaQuestão 18
Considere uma amostra de tempos de falha de um componente elétrico (meses) que tenha gerado o seguinte boxplot:
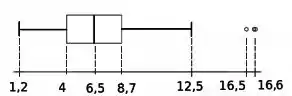
c) Encarando agora esse boxplot como se ele fosse uma distribuição de probabilidade, ou seja, encarando os quartis amostrais como se fossem quartis populacionais, suponha que componentes sejam sorteados (com reposição e de modo independente) e que se anote o tempo que levou até o componente falhar. Usando o TCL, obtenha uma aproximação para a probabilidade de observarmos mais de componentes cujos tempos de falha tenham sido menores que meses.
Ver solução completa