Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Medidas de Dispersão

Ver Todos os Exercícios

Teoria

As medidas de dispersão são amplitude, variância e desvio padrão e coeficiente de variação. Elas são usadas pada determinar a variação em um grupo de dados em relação à sua média.

O que são as Medidas de Dispersão?

Medidas de dispersão são parâmetros utilizados na estatística pra determinar a variação dos dados em um conjunto de valores.

-Beleza, mas pra que usamos as medidas de dispersão? 😖

Pra ficar mais claro pra que servem as medidas de dispersão, eu quero que você imagine a seguinte situação:

Você tem um professor de Probest muito carrasco, que pesa muito a mão na hora da correção e quase todo mundo da turma fica com uma nota super baixa:

Exemplo de nota dos Alunos de Probabilidade e Estatística.
Exemplo de nota dos Alunos de Probabilidade e Estatística.

Você quer fazer uma reclamação na coordenação, mas que tipo de dados você poderia entregar pra eles? Afinal a média da turma é baixa, mas se todo mundo tivesse tirado 5, não seria o fim do mundo!

O problema aqui é que a média, que é uma medida de tendência central, não expressa da melhor maneira a realidade das notas da turma. Então é a hora das medidas de dispersão brilharem!

As medidas de dispersão tornam a análise estatística mais confiável e completa!

Amplitude

A amplitude é a diferença entre o maior e o menor valor em um conjunto de dados.

Para o nosso exemplo ali de cima, a amplitude seria:

Esse dado não prova muita coisa, mas ajuda a gente perceber que existe uma discrepância bem grande entre as notas!

Variância

Existem dois tipos de variância, a variância populacional que leva em conta os dados de toda a população e a variância amostral , que como o próprio nome indica, leva em conta os dados de uma amostra.

Variância populacional

A variância populacional pode ser calculada a partir da seguinte fórmula:

Onde é um valor observado, é a média entre todos os valores da população e é o número de elementos da população.

No nosso exemplo, a população é a turma de probest. Como temos poucos dados e temos acesso a todos eles, podemos calcular a variância populacional:

A variância das notas de probest é alta, isso significa que o conjunto de dados varia muito entre si, ou seja, os dados são dispersos.

Variância Amostral

Beleza, mas e se não estivéssemos analisando só uma turma de probest? E se quiséssemos saber a média de todos os alunos que fazem essa matéria no Brasil?

Como teríamos acesso a todos esses dados?!

A solução é simples, a gente pode trabalhar com uma amostra!

A variância amostral pode ser calculada usando a seguinte fórmula:

Essa fórmula é bem parecida com a variância populacional, a diferença é o que aqui significa o número de elementos na amostra. Além disso quando subtraímos do estamos diminuindo o grau de liberdade.

Desvio Padrão

O desvio padrão é a raiz quadrada da variância, então também existem dois tipos de desvio padrão, o desvio padrão populacional e o desvio padrão amostral .

Desvio padrão populacional

Podemos calcular o desvio padrão populacional a partir da seguinte fórmula:

Desvio padrão amostral

Para calcular o desvio padrão amostral, fazemos:

Coeficiente de Variação Amostral

O coeficiente de variação é simplesmente a razão entre o desvio padrão e a média amostral :

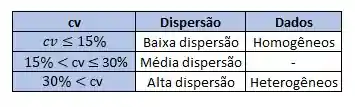
O coeficiente de variação é usado para analisar a dispersão em termos relativos a seu valor médio quando duas ou mais séries de valores apresentam unidades de medidas diferentes. Sacou?

Então, como o coeficiente de variação analisa a dispersão em termos relativos, ele será dado em . Quanto menor for o valor do coeficiente de variação, mais homogêneos serão os dados, ou seja, menor será a dispersão em torno da média. De uma forma geral, temos:

Dispersão e Coeficiente de variação
Dispersão e Coeficiente de variação

Medidas de Dispersão: Vídeo Aula

Ficou com alguma dúvida?!

Então se liga nesse vídeo super completo sobre as medidas de dispersão, que o Responde Aí preparou pra você!

Agora vamos praticar com exercícios?!

Amplitude

Variância

Desvio Padrão

Coeficiente de Variação Amostral

Medidas de Dispersão: Vídeo Aula

Exercícios Resolvidos

Exercício Resolvido #1

UERJ-LISTA 1- PROF FABIANO-1

Os dados da tabela abaixo são referentes a peso ( k g ) e comprimento ( d m ) de manilhas de cimento para uso em obras públicas. Calcule para as características avaliadas (peso e comprimento) as seguintes estatísticas:

  1. Variância e desvio-padrão;

Passo 1

(a)

Vamos usar:

s 2 = ∑ x i 2 - n . x ¯ 2 n - 1

Temos que:

x ¯ = ∑ i = 1 n x i n

Então peso:

x ¯ = 23 + 22,7 + … + 19,5 10 = 20,58

s x 2 = ( 23 2 + 22,7 2 + … + 19,5 2 ) - 10 × 20,58 2 9 = 14,2973

Comprimento:

y ¯ = 104 + 105 + … + 99 10 = 101,3

s y 2 = ( 104 2 + 105 2 + … + 99 2 ) ) - 10 × 101,3 2 9 = 17,7889

Passo 2

Desvio padrão é a raiz quadrada da variância, então:

Peso:

s x   = 14,2973 = 3,7812

Comprimento:

s y = 17,7889 = 4,2177

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #2

João Ismael D. Pinheiro, Probabilidade e Estatística: Quantificando a incerteza, Rio de Janeiro: Elsevier Editora Ltda, 2012, pp. 378 - 17

Será mera coincidência?

Considere o seguinte conjunto de dados:

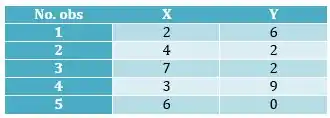
a) Calcule as variâncias amostrais de X e de Y, ou seja, S x 2   e   S Y 2

b) Construa uma nova variável Z = X + Y e calcule a sua variância amostral S z 2

c) Compare S z 2 com S x 2 + S y 2 + 2 S x y

d) Como você explica essa coincidência?

Passo 1

Queremos a Variância Amostral, portanto vamos usar:

s 2 = ∑ x i 2 - n . x ¯ 2 n - 1

Temos que:

x ¯ = ∑ i = 1 n x i n

Passo 2

  • Para X:

    • x - = 2 + 4 + 7 + 3 + 6 5 = 22 5 = 4,4

    Logo

    S x 2 = 2 2 + 4 2 + 7 2 + 3 2 + 6 2 - 5 × 4,4 2 5 - 1 = 114 - 5 × 19,36 4 = 17,2 4

    S X 2 = 4,3

    Passo 3

  • Para Y:

    • y - = 6 + 2 + 2 + 9 + 0 5 = 19 5 = 3,8

    Logo

    S Y 2 = 6 2 + 2 2 + 2 2 + 9 2 + 0 2 - 5 × 3,8 2 5 - 1 = 125 - 5 × 14,44 4 = 52,8 4

    S Y 2 = 13,2

    Passo 4

    b) Construa uma nova variável Z = X + Y e calcule a sua variância amostral S z 2

  • Para Z:

z - = 8 + 6 + 9 + 12 + 6 5 = 41 5 = 8,2

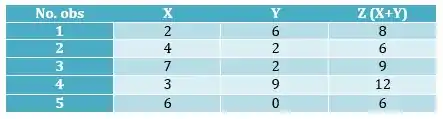
Logo

S Z 2 = 8 2 + 6 2 + 9 2 + 12 2 + 6 2 - 5 × 8,2 2 5 - 1 = 361 - 5 × 67,24 4 = 24,8 4 = 6,2

Passo 3

c) Compare S z 2 com S x 2 + S y 2 + 2 S x y

Agora vamos comparar o resultado obtido em S Z 2 com essa expressão dada.

Lembre-se que S X Y = C o v ( X , Y ) e que por sua vez

C o v X Y = ∑ i = 1 n x i y i - n x - y -   n - 1

Vamos calcular então S X Y :

C o v X Y = ∑ i = 1 n ( x i y i - n x - y - )   n - 1

= [ 2 × 6 + 4 × 2 + 7 × 2 + 3 × 9 + 6 × 0 - 5 4,4 × 3,8 ] 4

C o v X Y = S X Y = 61 - 83,6 4 = - 5,65

Então teremos:

S X 2 + S Y 2 + 2 S X Y = 4,3 + 13,2 + 2 × - 5,65 = 17,5 - 11,3 = 6,2

Ou seja,

S X 2 + S Y 2 + 2 S X Y = S Z 2

Passo 4

d) Como você explica essa coincidência?

Essa coincidência não é tããão coincidência assim. Se antes tínhamos a seguinte propriedade:

V a r X + Y = V a r X + V a r Y + 2 C o v ( X Y )

Agora temos na versão amostral

S X 2 + S Y 2 + 2 S X Y = S X + Y 2

Resposta

a)   17,2 4 e 52,8 4

b) 6,2

c) S X 2 + S Y 2 + 2 S X Y = S Z 2

d) Se antes tínhamos a mesma relação para as variâncias, teremos para as variâncias amostrais.

Exercício Resolvido #3

EACH, USP – Slides Prof. Camilo Rodrigues Neto

Suponha que parafusos a serem utilizados em tomadas elétricas são embaladas em caixas rotuladas como contendo 100 unidades. Em uma construção, 10 caixas de um lote tiveram o número de parafusos contados, fornecendo os valores 98 ,   102 ,   100 ,   100 ,   99 ,   97 ,   96 ,   95 ,   99   e   100 . Calcule as medidas resumo de dispersão.

Passo 1

Começando pela variância:

s ² = ∑ i = 1 n ( x i - x - ) ² n - 1

Calculando a média dos dados, vemos que:

x - = 98,6

Então...

s 2 = 98 - 98,6 2 + 102 - 98,6 2 + 100 - 98,6 2 + 100 - 98,6 2 10 - 1

+ 99 - 98,6 2 + 97 - 98,6 2 + 96 - 98,6 2 + 95 - 98,6 2 + 99 - 98,6 2 + ( 100 - 98,6 ) ² 10 - 1

s ² = 4 , 49

Passo 2

E o desvio padrão é a raiz dissaê...

s = 4,49 = 2 , 12

Resposta

s ² = 4 , 49

s = 2 , 12

Exercício Resolvido #4

EACH, USP – Slides Prof. Camilo Rodrigues Neto

Numa classe com 12   alunos de um curso de inglês, os alunos indicaram o número de outras línguas (além de português e inglês) com que tinham alguma familiaridade. O resultado foi o seguinte :   0 ,   0 ,   0 ,   0 ,   1 ,   1 ,   1 ,   1 ,   1 ,   2 ,   2   e   4 . Obtenha as medidas resumo de dispersão (variância e desvio padrão).

Passo 1

Primeiro vamos calcular a média:

x - = 0 + 0 + 0 + 0 + 1 + 1 + 1 + 1 + 1 + 2 + 2 + 4 12 = 1,08 3

Então a variância:

s ² = ∑ i = 1 n ( x i - x - ) ² n - 1

s ² = 0 - 1,08 3 2 × 4 + 1 - 1,08 2 × 5 + 2 - 1,08 2 × 2 + 4 - 1,08 2 12 - 1

s ² = 1 , 3561

E o desvio padrão, é só tirar a raiz da variância:

s = 1,3561 = 1,1 645

Resposta

s ² = 1,3561

s = 1,1645

Exercício Resolvido #5

Elaboração Própria

Medidas as estaturas de 1017 indivíduos, obtivemos média de 162,2   c m e desvio padrão de 8,01   c m . O peso médio desses mesmos indivíduos é 52   k g , com um desvio padrão de 2,3   k g . Esses indivíduos apresentam maior variabilidade em estatura ou em peso?

Passo 1

Toda vez que for falado de maior variabilidade estamos lidando com o coeficiente de variação c v ! Por que ele dá pra gente o quanto uma medida está variando em relação a própria média.

Sabendo disso, vamos calcular o c v para as estaturas:

c v = s x - = 8,01 162,2 = 0,0494 → 4,94 %

E para os pesos:

c v = s x - = 2,3 52 = 0,0442 → 4,42 %

Passo 2

Como o c v da estatura é maior, a maior variabilidade é da estatura!

4,94 % > 4,42 %

Resposta

A   e s t a t u r a .

Exercícios de Livros Relacionados

Nos exercícios 29 e 30, use a Regra Empírica.O valor médio da TV via satélite de uma amostra de domicílios era de $70,00 por mês com desvio padrão de $14,50 por mês. Entre quais dois valores encontram
De uma amostra aleatória de domicílios, listamos o número de aparelhos de televisão. Encontre a média e o desvio padrão amostral dos dados.Números de televisores 0 1 2 3 4 5Números de domicílios 1 8 1
Raciocínio gráfico. Compare os três conjuntos de dados. (a) Sem calcular, determine qual conjunto de dados tem o maior desvio padrão amostral e qual tem o menor. Explique seu raciocínio.(b) De que man
Por que o desvio padrão é usado com mais frequência do que a variância?
Encontrando estatísticas amostrais. Encontre a amplitude, a média, a variância e o desvio padrão para a amostra dada.Tempo de gestação. A duração (em dias) da gravidez para uma amostra aleatória de mã