Exercícios de Medidas de Dispersão - Lista de Exercícios Resolvida

Será mera coincidência?

Considere o seguinte conjunto de dados:

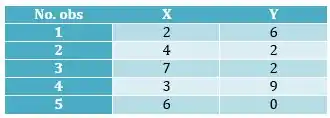
a) Calcule as variâncias amostrais de X e de Y, ou seja,

b) Construa uma nova variável e calcule a sua variância amostral

c) Compare com

d) Como você explica essa coincidência?

Os dados da tabela abaixo são referentes a peso e comprimento de manilhas de cimento para uso em obras públicas. Calcule para as características avaliadas (peso e comprimento) as seguintes estatísticas:

1. Variância e desvio-padrão;

Medidas as estaturas de indivíduos, obtivemos média de e desvio padrão de . O peso médio desses mesmos indivíduos é , com um desvio padrão de . Esses indivíduos apresentam maior variabilidade em estatura ou em peso?

Suponha que parafusos a serem utilizados em tomadas elétricas são embaladas em caixas rotuladas como contendo unidades. Em uma construção, caixas de um lote tiveram o número de parafusos contados, fornecendo os valores . Calcule as medidas resumo de dispersão.

Numa classe com alunos de um curso de inglês, os alunos indicaram o número de outras línguas (além de português e inglês) com que tinham alguma familiaridade. O resultado foi o seguinte. Obtenha as medidas resumo de dispersão (variância e desvio padrão).

Determinada indústria suspeita que está recebendo, de um certo fornecedor, peças de aço fora das especificações. Ela decidiu então avaliar a quantidade de carbono e a dureza do aço de tais peças. Para isso, usou nove peças e obteve as seguintes medidas:

1,41 1, 24 0,95 1,13 1,21 1,32 1,05 1,02 1,29

386 364 331 353 365 374 341 335 369

1. O fornecedor do aço diz que o teor de carbono deve ser de . Calcule a média amostral e o desvio padrão amostral do teor de carbono. Use os valores obtidos, e apenas os seus conhecimentos de Análise Exploratória, para comentar se há evidências contra ou a favor da afirmação do fornecedor.

Para facilitar: , e .

Uma empresa deseja estudar a influência da propaganda sobre a venda de seus produtos. Para isso, obteve os seguintes dados relativos a 5 produtos seus:

10 20 30 40 50

10 10 20 20 40

onde é o investimento em propaganda (em milhares de reais) e é o valor da venda do produto (em milhões de reais). Pede-se:

1. Correlação entre e ; um gráfico de dispersão de e ;
2. Valores estimados (por mínimos quadrados) dos parâmetros da reta ;
3. Valor estimado da venda quando a propaganda é 35 mil reais. Forneça uma interpretação do coeficiente no contexto deste problema.

A tabela abaixo apresenta o número de gols sofridos pela seleção brasileira de futebol em cada uma das edições da copa do mundo.

1. Qual é o número médio de gols sofridos pela seleção por edição da copa? Calcule o desvio padrão e o coeficiente de variação do número de gols sofridos.

Temos dois conjuntos de dados:

•, de tamanho, cuja média é e cuja variância é ; e

•, de tamanho , cuja média é e cuja variância é ; e

eles foram unidos para formar um novo conjunto de dados de tamanho, cuja média é e cuja variância é .

(a) Calcule média e variância do conjunto de dados: 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1.

(b) Prove que

(c) Prove que

Sugestão: use as identidades: e No 1° somatório faça e , ficando com . Faça algo análogo com o 2° somatório.

(d) Usando o que deve ser provado nos itens (b) e (c), recalcule a média e a variância do conjunto de dados do item (a). Desta vez, divida os dados em um primeiro conjunto com as 5 primeiras observações e um segundo conjunto com as 7 últimas observações

Na tabela a seguir apresentam-se algumas estatísticas descritivas dos preços de venda (em dólares americanos) de cinco moedas nos últimos 12 meses:

Qual destas moedas apresentou a maior variação relativa, ou seja, o coeficiente de variação no período?