Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 31b
Com base em experiências anteriores, a Companhia Telefônica sabe que das contas dos seus clientes em uma comunidade são pagas com atraso. Para os itens abaixo, compare a solução exata com aquela obtida através de aproximação da variável aleatória pela distribuição normal.
- Se 150 contas são enviadas mensalmente para a comunidade, encontre a probabilidade de que 17 ou mais sejam pagas com atraso
Passo 1
Mais uma vez, não custa nada relembrar:
E que
Ou seja, de tentativas, temos de chance de sucesso( no caso sucesso significa pagar conta com atraso)
Se você se lembrar, uma binomial pode ser calculada por:
Para qualquer distribuição binomial, temos o seguinte:
E
Passo 2
Começando pelo cálculo exato,
Queremos:
Lembrando que só podemos usar a binomial quando temos o sinal de igual; pois bem, isso significa uma m****a bem grande:
Falta-me coragem; você também nem deveria tentar.
Mas caso queira, a solução será algo do tipo:
E então:
Passo 3
Uma dica: Abandona, não faz sentido ficar calculando isso; vamos usar direto a aproximação pela normal:
E Lembrando também que precisamos aplicar a correção de continuidade, de acordo com a seguinte regrinha:
Portanto, nessa alternativa estamos buscando:
E aplicando a aproximação pela normal padrão:
Sabemos que a média e a variância de uma distribuição BINOMIAL são dadas por:
E
Substitindo:
Lembrando das propriedades da tabela/gráfico da distribuição Normal, teremos:
Como o gráfico é simétrico:
Precisamos buscar na tabela:
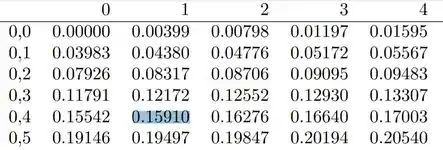
Portanto, encontramos:
E então:
Resposta
Concluindo, se você tiver coragem verá que calculando a partir da binomial vamos encontrar algo muito próximo disso (Ah não diga!!).
Pela binomial , e usando a aproximação pela normal