Medidas de Centralidade e Dispersão para V.A. Discreta
Produzido por Jorge Alberto NascimentoTeoria
Introdução
Quando temos um estudo estatístico, é muito importante ter ferramentas para poder interpretar os dados obtidos.
Por exemplo, considere uma universidade com 10.000 estudantes de engenharia e considere uma v.a. número de aprovações que um aluno selecionado teve no período passado. A função de probabilidade de está representada na tabela abaixo.

Onde são os eventos e é a probabilidade de cada evento acontecer.
Como podemos “resumir” os dados dessa tabela? Podemos utiizar o valor médio, concorda?!
Beleza, mas se eu te perguntasse qual é o valor médio de aprovações por aluno, ou seja, qual é o valor médio de , você surtaria??? Calma que eu to aqui pra te ajudar!!!!!
Imagina como seria se todos precisassem estudar estatística a fundo para interpretar uma tabela de dados??

Melhor não, né?
É por isso que existem as medidas de Centralidade e Dispersão! São ferramentas que vão ajudar a gente a entender o que de fato aqueles dados significam, indicam etc…
Preparados?!
Esperança
Vamos tentar entender a ideia com o exemplo do início:
Poderíamos calcular a média multiplicando o número de aprovações pelo respectivo número de alunos e dividir pelo total de alunos, certo? Aquela média do ensino médio.
Beleza, temos uma média dos valores certo? Porém, e se perguntassem qual o valor esperado de aprovações?
Valor esperado remete a probabilidade de tal coisa acontecer certo? E daí que vem a medida Esperança .
é considerado uma medida de centralidade. Basicamente nos diz o seguinte: Se tivéssemos cada vez mais alunos qual seria a média esperada de aprovação? A resposta seria A esperança de .
No nosso exemplo a Esperança de é calculada multiplicando o número de aprovações () pela sua respectiva probabilidade(), ou seja:
Isso pode significar que a maioria dos alunos foi aprovado em mais ou menos 4 matérias, ou então que muitos foram aprovados em 6 e muitos foram aprovados em 2, o que nos daria a mesma média.
Com essa ideia temos a esperança de que é calculada como:
Beleza?!
Nesse caso temos que a Esperança deu um valor igual a Média, porém isso nem sempre é verdade!

Vamos ver mais um exemplo pra entender melhor?!
Exemplo
Consideremos o lançamento de um dado equilibrado. Seja a variável aleatória tal que:
Vamos calcular a esperança de ?
Sabemos que os valores possíveis de são e cada um tem de probabilidade de acontecer. Desse modo:
Observe o valor que encontramos, não é um valor possível para (não tem como um dado dar ). A esperança significa que se jogássemos o dado várias e várias vezes e depois calculassemos a média aritmética ESPERARÍAMOS que a média ficasse próxima a . Deu pra pegar a ideia? rs
Com isso vimos que nem sempre saber a esperança é o suficiente pra gente ter uma ideia clara da distribuição de . Ainda bem que existem outras ferramentas!

Variância e Desvio Padrão
Vamos começar pela variância!
Lembra que no exemplo anterior, quando calculamos a esperança chegamos a duas conclusões? Que ou a maioria dos alunos foi aprovado em mais ou menos 4 matérias, ou então que muitos foram aprovados em 6 e muitos foram aprovados em 2.
A variância pode nos dizer qual das duas opções é a certa!!
Calcular a variância é a mesma coisa que calcular o quão longe em geral os seus dados estão do valor esperado. Ou seja, ela mostra onde está concentrado a maioria dos seus dados, mais perto da média ou não.

A variância se calcula desse jeito:
- Variância – ou :
- Desvio padrão – ou :
Assim,
Ah, Se preferir podemos manipular essa fórmula:
Utilizando essa manipulação na fórmula, teremos
Assim,
Qualquer uma dessas fórmulas chegará no valor da variância...
Isso significa que a maioria dos nossos dados não estão tão afastados assim da Esperança, então podemos supor que a maioria dos alunos foi aprovado em mais ou menos 4 matérias.
Mas e o tal desvio padrão?
Ele também é uma medida de dispersão. O desvio padrão também informa se os dados estarão perto ou não do valor esperado, porém de uma maneira mais geral. Um alto desvio padrão indica que os pontos dos dados estão espalhados no gráfico.
Se calcula da seguinte forma:
Existe também um outro jeito de medir essa variação, que é através do coeficiente de variação ou que indica a variabilidade em relação à média da população.
Se você reparar, o desvio padrão e coeficiente de variação deram números muito pequenos, então isso reforça a ideia de que a maioria dos alunos foi aprovado em mais ou menos 4 matérias.
É, são fórmulas e mais fórmulas, mas com o tempo se pega o jeito! Abaixo temos uma tabelinha para nos ajudar!!

Legal, né?! Com essas medidas fica fácil analisar e interpretar gráficos!

Vamos fazer mais exercícios?!
Esperança
Exemplo
Variância e Desvio Padrão
Exercícios Resolvidos
Exercício Resolvido #1
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 139-10
Considere o lançamento de três moedas. Se ocorre o evento CCC, dizemos que temos uma sequência, ao passo que se ocorre o evento CRC temos três sequencias. Defina a v.a. X = número de caras obtidas e Y = número de sequências, isso para cada resultado possível. Assim, e . Obtenha as distribuições de X e Y. Calcule E(X), E(Y), Var (X) e Var (Y).
Passo 1
Vamos lá então!
Primeira coisa que temos que fazer é: Escrever a distribuição de probabilidade tanto da v.a. X quanto da v.a. Y certo?
Pra isso temos que listar os eventos:
Esse aí é o nosso espaço amostral .
Passo 2
Agora vamos entender quem é a v.a. X: número de caras obtidas e analisar os eventos:
1º evento: RRR
2º Evento: RRC
Note que o 2º evento = 3º evento = 4º evento Temos duas coroas e apenas uma cara? Ou seja, eles são as permutações possíveis certo? Então podemos falar que:
5º evento: RCC
Note que teremos um caso parecido com o evento 2. Note que o:
5º evento = 6º evento = 7º evento
Ou seja, temos nesses três casos uma coroa e duas caras. Esses casos são a permutações possíveis, então podemos falar que:
8º evento: CCC
Assim, podemos montar a tabela de distribuição de X:
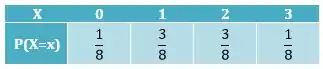
Passo 3
A partir disso podemos calcular E(x) e Var(x)
Passo 4
Agora vamos fazer o mesmo passo a passo para a v.a. Y: número de sequências
1º evento: RRR
2º Evento: RRC
3º Evento: RCR
4º Evento: CRR
5º evento: RCC
6º Evento: CRC
7º Evento: CCR
8º evento: CCC
Montando a tabela de distribuição de Y:

Passo 5
A partir disso podemos calcular E(y) e Var(y)
Resposta
Exercício Resolvido #2
UERJ-lista 1 prof Fabiano-18(a)
Uma transportadora de cargas possui quatro caminhões de aluguel. O aluguel é realizado por dia e que a distribuição diária do número de caminhões alugados por dia é dada por:

Sabendo que o aluguel por dia é da ordem de e que a despesa total diária com a manutenção de cada veículo é igual a quando este é alugado e de , quando tal fato não ocorre, encontre:
- O número médio diário de caminhões alugados e o desvio padrão.
Passo 1
(a)
Se a gente chamar de a v.a. que representa o número de caminhões alugados por dia. A gente já tem a tabela com os valores possíveis para (0,1,2,3,4) e suas respectivas probabilidades.
Pra calcular o número médio de caminhões alugados é só calcular:
Passo 2
Pra calcular a variância usamos a fórmula:
Aí agora podemos calcular o desvio padrão que é a raiz quadrada da variância:
Resposta
Exercício Resolvido #3
UERJ-lista 1 prof Fabiano-19
Os funcionários de uma certa empresa, , , e ganham 1, 2, 2 e 4 salários mínimos respectivamente. Retiram-se amostras com reposição de 2 indivíduos e, mede-se o salário médio da amostra retirada. Calcule a média, o desvio padrão e o coeficiente de variação do salário médio amostral
Passo 1
Bom, vamos fazer que nem o exercício pede.
Montar todas as possíveis amostrar com 2 indivíduo, com reposição, o que significa que pode ter duas vezes o mesmo indivíduo. E ir medindo o salário médio de cada amostra.
Vou montar uma tabela marota!
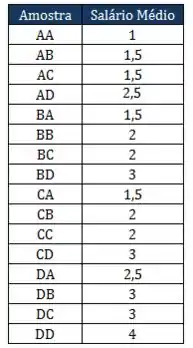
O salário médio é só somar o salário dos dois indivíduos de cada amostra e dividir por 2.
Passo 2
Se é a v.a. que representa o salário médio das amostras possíveis.
A gente consegue perceber que é uma v.a. discreta que pode assumir valores específicos, no caso: 1,0; 1,5; 2,0; 2,5; 3,0; 4,0.
Podemos montar uma tabela com a distribuição de probabilidades de cada um desses possíveis valores de .
Essa tabela vai nos ajudar a calcular o que precisamos.
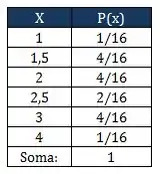
Passo 3
Pra calcular a média, ou esperança, vamos usar a fórmula:
Passo 4
Para a variância, vamos usar:
Passo 5
Agora podemos calcular o desvio padrão:
Passo 6
Pra fechar, o coeficiente de variação.
Resposta
Exercício Resolvido #4
UFRJ-P1-2014.2.-2(a)(b)
Três bolas enumeradas e estão num balde. Sorteamos duas bolas com reposição, e somamos os valores obtidos. Seja este valor.
- Obter a função de probabilidade, a esperança e a variância de .
- Refazer o item a) se as bolas forem sorteadas sem reposição.
Passo 1
é o valor da soma das duas bolas sorteadas, beleza? Temos primeiro que montar a função de probabilidade de .
Quais são os possíveis valores de ? Se é a soma de duas bolas retiradas com reposição e as bolas são e , então os possíveis valores são:
Note que , a ordem importa. Então a gente tem combinações de resultados pra retirada das duas bolas.
Desse jeito a gente tem que os possíveis valores de são: .
Nossa variável é uma v.a. discreta, concorda? Seus possíveis valores são números fixos, não tem como a soma das duas bolas resultar em !
Passo 2
Pra montar a função de probabilidade de uma v.a. discreta, a gente precisa montar aquela tabelinha, com os possíveis valores de e a probabilidade de cada um desses valores acontecer.
Os possíveis valores a gente já tem: .
Agora falta calcular a probabilidade de cada um, que é tranquilo.
Vamos começar por .
A soma das duas bolas só resulta em em uma das combinações de bolas, quando sai , daí:
Pensando dessa mesma forma a gente consegue todas as prob. que a gente quer.
Você pode até conferir se tá tudo certin, é só ver se a soma de todas as probabilidades dá .
Você pode deixar sua resposta final assim, ou se tiver com tempo sobrando, colocar arrumado numa tabela maneira.
Passo 3
Vamos calcular a esperança da variável.
É só multiplicar os possíveis valores de pela respectiva probabilidade dele acontecer.
Passo 4
Pra variância é só usar a fórmula abaixo:
Passo 5
(b)
Po, agora vai ser sem reposição, o que que muda? Muda que resultados como e não vão ser possíveis, certo?
Então os únicos resultados possíveis são:
E assim, os possíveis resultados pra nossa v.a. soma das duas bolas, vai ser:
Passo 6
Agora é o mesmo esquema pra calcular a probabilidade de cada resultado possível de .
É isso aí, dá pra você organizar numa tabela se preferir.
Passo 7
Vamos calcular esperança e variância de novo...
Passo 8
Variância:
Resposta
Exercício Resolvido #5
Elaboração Própria
Suponha que lancemos três moedas, e que o resultado cara representa o número 2 e o resultado coroa representa o número 3. Agora suponha que temos uma variável aleatória discreta que represente a soma dos valores sorteados nas moedas. Qual a variância dessa variável?
Passo 1
Vamos chamar de:
Vamos listar todas as combinações que podemos ter no lançamento das moedas:
Então esses daí são os valores que nossa variável pode assumir. Calculando a probabilidade de cada valor ocorres:
Passo 2
Vamos começar calculando a esperança de :
E a variância vai ser dada por:
Vamos calcular separadamente:
Então a variância é: