Desenhe a imagem da superfície parametrizada dada por
Passo 1
Vamos encontrar a equação da superfície não parametrizada, assim, devemos fazer as substituições:
Passo 2
Substituindo os valores de na expressão do a gente vai ter isso aqui
Passo 3
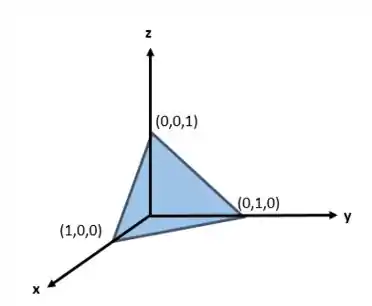
Temos que a imagem é um plano que é delimitado pelas desigualdades previstas no enunciado.
Que passando para as variáveis , e temos:
Agora a última desigualdade a gente pode fazer o seguinte
Passo 4
A imagem da superfície parametrizada será:
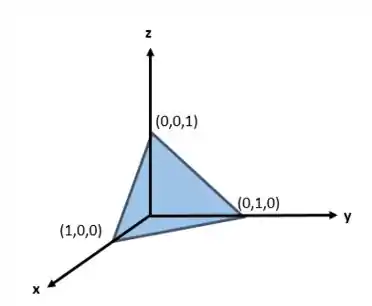
Resposta
Exercícios de Livros Relacionados
Determine uma equação do plano tangente à superfície parametrizada dada no ponto especificado. Desenhe a superfície e o plano tangente. r u , v = 1 - u 2 - v 2 i ⃑ - v j ⃑ - u k ⃑; ( - 1 , - 1 , - 1 )
Determinar uma equação vetorial da reta normal às seguintes superfícies nos pontos indicados.d) r → u ,v = u ,v ,1 - u - v ; P 1 4 , 1 4 , 1 2
Escrever uma equação vetorial para a superfície dada e determinar as equações do plano tangente e da reta normal, nos pontos indicados.c) z = x y ; P 0 1 , 1 2 , 1 2 ;P 1 ( 0 , 2 ,0 )
Determinar uma equação vetorial da reta normal às seguintes superfícies nos pontos indicados. r → u ,v = u 2 + v 2 - 1 ,u ,v ; P ( 4,1 , 2 )
Determine a equação do plano tangente à superfície parametrizada dada no ponto especificado. Se você tiver um programa que trace o gráfico de superfícies parametrizadas, use-o para traçar a superfície