Exercícios de Reta Normal e Plano Tangente - Lista de Exercícios Resolvida

Desenhe a imagem da superfície parametrizada dada por

Encontre a equação da reta normal e do plano tangente à superfície parametrizada por no ponto

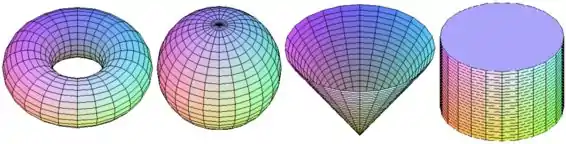
Quais superfícies dadas na figura abaixo correspondem às parametrizações II e IV:

Encontre a equação da reta normal e do plano tangente ao cone no ponto

Encontre a parametrização da reta normal e o plano tangente à superfície parametrizada por no ponto em que e

2) Seja uma superfície parametrizada por e

1. Identifique essa superfície
2. Encontre uma equação da reta normal a em
3. Encontre uma equação do plano tangente a em

Quais superfícies dadas na figura abaixo correspondem às seguintes parametrizações.

Diga quais as parametrizações da curvas da grade para as superfícies parametrizadas por e por e a que correspondem.