Encontre a série de Taylor em torno de para as funções:
Passo 1
Lembrando que a série de Taylor é definida por:
Em torno de temos:
O que temos que fazer agora é tentar achar um padrão no valor das derivadas de cada . Vai ficar mais claro quando vocês verem sendo feito haha.
Passo 2
Vamos começar escrevendo o valor de algumas derivadas de :
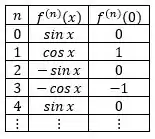
Por essa tabela conseguimos pegar o seguinte padrão, só os termos de ímpar vão aparecer na série pois os de par são sempre zero. E os componentes de termo ímpar vão trocando de sinal!
Podemos substituir todos os na fórmula por para pegarmos apenas os ímpares. E usando o termo para cuidar da troca de sinal ficamos com:
Passo 3
Essa provavelmente vai ficar bem parecida com a do seno né? Fazendo a mesma tabelinha:
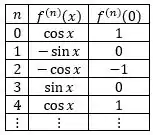
O padrão é praticamente o mesmo, mas dessa vez temos apenas os pares! Então vamos trocar por pra pegar só os pares e manter o termo pra troca de sinais.
Passo 4
Montamos a tabelinha de novo:

E aí, essa tabela ta te lembrando alguma coisa? Pra mim ela ta igualzinha ao fatorial de né? Então nossa série vai ficar:
Passo 5
Precisa nem de tabela pra dizer o que vai acontecer aqui né? Independente do , vai valer sempre . Logo, a série de Taylor vai ficar:
Passo 6
Esse não ta tão óbvio quanto o último né? Vamos para a nossa tabelinha de novo:

Vamos passo a passo. Repara como os termos estão trocando de sinal sempre que mudamos o ! E que para ímpar o sinal é positivo. Logo, teremos um termo na nossa série de Taylor.
Outra coisa importante é que temos de novo aquela cara de fatorial! Só que agora para apareceu o fatorial de . Então tem que ter um na jogada.
Dessa forma, nossa expressão genérica para deve ser
Essa fórmula só não bate com o resultado de , mas como para esse temos nem precisamos contar ele! Nossa série de Taylor ficaria então:
Repare que começamos em ao invés de justamente para eliminar aquela primeira linha da tabela. Outro detalhe importante é que podemos decompor em
Assim ficamos com:
É comum iniciarmos a série com , para isso basta trocarmos os por :
Ufa, esse é o valor final da nossa série de Taylor!