Exercícios de Série e Polinômio de Taylor - Lista de Exercícios Resolvida

Encontre , usando série de Taylor gerada por em , sabendo que:

Encontre , usando série de Taylor gerada por em , sabendo que:

Obtenha as aproximações linear e quadrática para , em torno de usando a fórmula de Taylor.

Em um mesmo gráfico, esboce a curva e as aproximações linear e quadrática obtidas em . Através do gráfico analise o comportamento das aproximações constando que representam apenas localmente. Qual das duas curvas você escolheria para aproximar em torno de .

Obs.: Os gráficos podem ser esboçados a mão ou traçados usando software ou ainda na calculadora.

Use um polinômio de Taylor em torno de para aproximar com uma acurácia de .

Encontre a série de taylor de em .

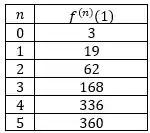
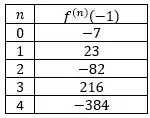
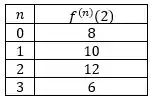
Seja .

Encontre o polinômio de Taylor de grau em torno de .

Encontre um limitante para o erro e o erro exato de .

Repita o item usando .

Repita o item usando o polinômio do item .

Mostre que a função pode ser representado como série de Taylor em torno de para todo

Encontre a série de Taylor em torno de para as funções:

Encontre a série de Taylor de em torno de :

Encontre , usando série de Taylor gerada por em , sabendo que:

Considere a seguinte função

e determine:

1. o polinômio de Taylor de grau em torno de para aproximar
2. a aproximação do item (a) para calcular o valor aproximado de para ;