Mostre que a função pode ser representado como série de Taylor em torno de para todo
Passo 1
Lembrando que a série de Taylor é definida por:
Em torno de temos:
O que temos que fazer agora é tentar achar um padrão no valor das derivadas de .
Passo 2
Vamos montar uma tabelinha para as derivadas de e seus valores no ponto :
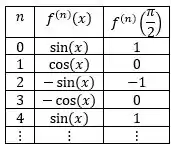
Por essa tabela conseguimos perceber o seguinte padrão: só os termos de par vão aparecer na série pois os de ímpar são sempre zero. E os componentes de termo par vão trocando de sinal!
Podemos substituir todos os na fórmula por para pegarmos apenas os pares. E usando o termo para cuidar da troca de sinal ficamos com:
Prontinho!! Essa é a nossa série de Taylor!
E perceba que ela não possui restrições, portanto é definida para qualquer .