Teorema de Stokes
Calcule a integral de linha de campo vetorial , onde é a curva parametrizada por e
Dica: Usar Teorema de Stokes.
Passo 1
Bom, se a questão falou para a gente usar Teorema de Stokes, vamos confiar né, gente. Antes de tudo, vamos calcular o rotacional desse campo:
Opa, campo conservativo, né? MUITA CALMA NESSA HORA, GENTE.
Temos uma indeterminação no campo quando (o denominador dá zero), ou seja, ao longo do eixo . Por isso, não podemos usar os conceitos de campos conservativo aqui, por isso a questão mandou a gente uar Stokes, sacou?
Passo 2
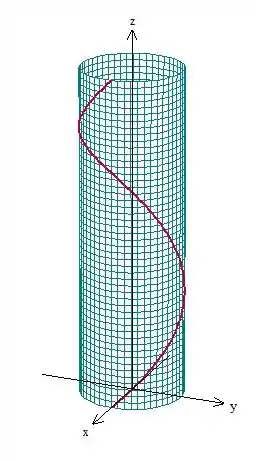
Ok, vamos usar Stokes. A curva do problema é mais ou menos isso aqui:

Ela vai “girando” em torno do eixo (dá pra ver isso pelas coordenadas e ) ao mesmo tempo que vai “subindo” na direção , podemos ver isso por .
É importante fazer esse esboço para conseguirmos montar o problema. Ok, vamos aplicar Stokes na superfície que fica “abaixo” de :
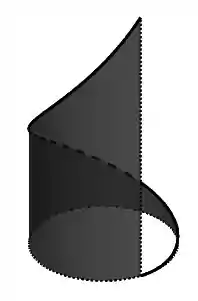
Reparou que essa superfície está dentro de um cilindro, né? É mais ou menos isso aqui:
É como se cortasse o cilindro. Então se é esse pedaço de cilindro, precisamos identificar suas fronteiras. Deu pra perceber que não é só , né? Temos três fronteiras:
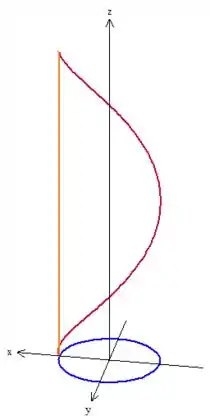

Percebeu? Temos um segmento de reta vertical, que liga os pontos inicial e final de , temos e também uma circunferência em (a base do cilindro).
Temos então:
A fronteira é isso tudo. Então, aplicando Stokes:
Como gira no sentido anti-horário ( vai de a ), pela Regra da Mão Direita, para ser orientada positivamente, sua normal deve apontar para dentro.
Sendo assim, aplicando novamente a regra para as outras curvas, o segmento está orientado para baixo e a circunferência gira no sentido horário.

Como o rotacional é nulo:
Passo 3
Agora precisamos das integrais nessas duas curvas. Vamos começar com o segmento de reta.
Antes de tudo: que pontos ele liga? Vamos olhar de novo a parametrização de :
Repare que os pontos inicial e final são:
Portanto, eles estão um “em cima” do outro, tem o mesmo e , só diferem na coordenada (por isso sabemos que o segmento é vertical). Show, agora vamos parametrizar isso aí.
Como o segmento é paralelo ao eixo , com e , podemos parametrizar assim:
Onde vai de a .
Derivando isso aí, temos:
Aplicando a fórmula:
O que nos dá:
Passo 4
Agora vamos para a circunferência no plano . Como a gente viu que o segmento de reta tem 1, podemos entender que o raio do cilindro que contém as curvas todas é , maaaas, se você não percebeu por aí, podemos ver o seguinte:
Olha as parametrizações de e de , isso não é uma circunferência de raio ? Quer dizer que a projeção de no plano é essa circunferência:
Show? Parametrizando em coordenadas polares com :
Como o sentido é horário, vai de a .
Derivando isso aí:
Agora, aplicando a fórmula:
Temos:
Passo 5
Agora, juntado tudo o que temos: