Calcule
Sendo a intersecção de com , orientada de modo que sua projeção no plano seja percorrida uma vez no sentido horário.
Passo 1
Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. Temos um cone com centro em cortado por um plano:
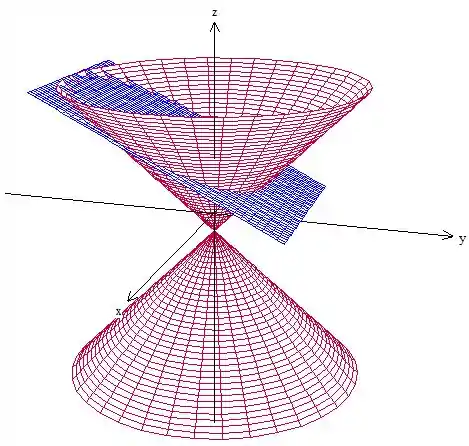
Esse desenho não precisa de precisão nenhuma, ok? É só para termos uma ideia mesmo, você pode desenhar um plano qualquer cortando o cone.
A questão pede para calcularmos a integral de linha em , que é a interseção do plano inclinado com o cone. Como podemos ver, forma uma elipse. Percebeu?
Passo 2
Ok, agora vamos analisar o problema. Reparou que a expressão do campo não é nem um pouco amigável, né? Imagina ainda substituir uma parametrização nisso aí, sem condições. Então vamos simplificar as coisas.
O Teorema de Stokes nos diz isso aqui:
Ou seja, podemos substituir essa integral de linha sobre a curva por uma integral do rotacional de sobre uma superfície que tenha a curva como fronteira. Ah, vamos usar o próprio retalho do plano em forma da elipse, né?
Agora vem o momento em que temos que tomar muito cuidado, olha a expressão do campo de novo:
Repare temos uma indeterminação quando e , portanto, o campo não está definido no eixo !
Então, não podemos usar o plano como superfíce, na verdade, não podemos usar nenhuma superfície que tenha apenas como fronteira por causa disso!
Ferrou, né. Não, vamos usar uma superfície que tenha como uma de suas fronteiras. Em vez de usar o plano, vamos usar um pedaço do cone, que também tem como fronteira, ok? Vamos cortar esse conwe com o plano :
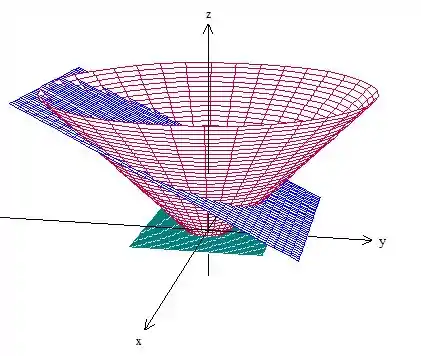
Então, é o pedaço do cone entre os planos e é a própria curva mais a borda debaixo do cilindro (uma circunferência).Temos então:
Agora vamos pensar nas orientações. Se está no sentido horário, pela Regra da Mão direita, deve ter vetor normal apontando para fora. Consequentemente, gira no sentido anti-horário.
Passo 3
Precisamos, então, calcular , sabendo que
Temos:
Passo 4
Como encontramos que o rotacional é nulo, temos:
Show?
Passo 5
Agora, para terminar a questão, precisamos calcular a integral de linha na outra borda da superfície, .
Como a circunferência está no plano , sua equação é dada pela intersecção entre e a equação do cone:
Parametrizando isso aí em coordenadas polares com , temos:
Como temos uma volta completa no sentido anti-horário, vai de a .
Essa última componente é porque a curva está no plano .
Certo, agora vamos derivar isso aí:
Agora vamos escrever o campo nas variáveis da parametrização e usar a fórmula:
Levando para ai ntegral, temos:
Passo 6
Temos então