Calcule , onde:
E é a intersecção de e , orientada de modo que a sua projeção no plano seja percorrida no sentido anti-horário.
Passo 1
Bom, vamos começar fazendo um esboço dessas superfícies para entender a questão. Temos um parabolóide elíptico virado para baixo com máximo em cortado pelo cilindro de parábola perpendicular ao plano :
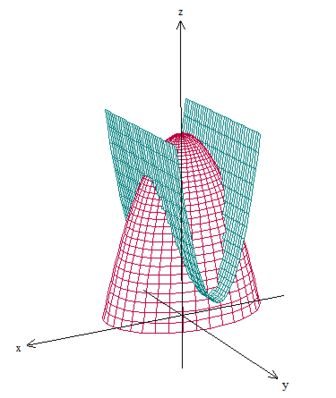
A curva do problema é essa formada pela interseção entre as duas superfícies. Para encontrar a sua expressão, vamos igualar as duas equações:
Uma elipse no plano .Mas isso é só a projeção da curva nesse plano, falta a coordenada , que pode ser dada tanto pela equação de uma superfície como a de outra. Vamos escolher a mais fácil, né:
Então, nossa curva vista de cima é uma elipse: guarde essa informação.
Passo 2
Ok, agora vamos analisar o problema. Reparou que a expressão do campo não é nem um pouco amigável, né?
Imagina ainda susbstituir uma parametrização nisso aí, sem condições. Então vamos simplificar as coisas.
Repara que os termos e são bem parecidos. Se a gente separar esse campo vetorial em duas partes (sendo uma delas apenas com essas parcelas), conseguimos um campo conservativo. Olha só:
Beleza? Então, podemos escrever:
Ou seja, primeiro vamos resolver separadamente o problema aplicando Stokes só com o campo , que é conservativo, depois só com o e, então, somar as respostas.
Passo 3
Para o campo
Vamos aplicar Stokes para trocar a integral de linha por uma de superfíce. Ecolhemos como superfícies esse retalho do paraboloide cortado pelo cilindro de parábola (a parte que fica abaixo do cilindro). Então:
Porque não escolhemos a parte de cima do paraboloide? Porque, se você reparar, o campo não está definido quando , ou seja, ao longo do eixo . Então, precisamos de uma superfície que não corte esse eixo!
Bom, mas essa superfície que escolhemos tem duas curvas como borda: em cima, (o que queremos) e embaixo uma elipse no plano , que vamos chamar de . Então, sendo :
Se gira no sentido anti-horário (no plano ), então, para termos orientação positiva, pela Regra da Mão Direita, tem vetor normal apontando para dentro e, consequentemente, gira no sentido horário.
Beleza, agora vamos calcular o rotacional desse campo:
Ainda bem que deu zero né, gente. Ótimo. Então, podemos escrever:
Precisamos agora calcular a integral de linha na elipse . Como é a base do paraboloide, para encontrar sua equação, “cortarmos” ele com o plano :
Tá, ferrou. Quando a gente parametrizar isso aí e substituir a parametrização no campo vai ficar uma porcaria, impossível de integrar. E agora?
Senta que agora vem a bruxaria. Lembra que no início da questão, nós vimos que a nossa curva, vista de cima, era uma elipse de equação ? Pode voltar lá pra checar, eu espero.
Então, se tem essa projeção, quer dizer que ela pertence ao cilindro , não é? Cilindro esse que não corta o eixo ... Agora olha a expressão do campo de novo.
Percebeu que é proporcional a ? Vamos então mudar a nossa superfície, você já vai entender o por que.
Vamos escolher esse cilindro de base elíptica, que tem como bordos a nossa curva e a sua base elíptica . Ou seja, temos isso aqui:
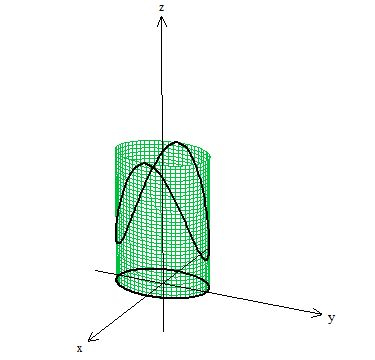
A superfície passa a ser então a parte desse cilindro verde que está entre a curva (em cima, orientada no sentido anti-horário) e a elipse (na base, orientada no sentido horário).
Isso não muda nada para o que fizemos até agora! Isso aqui continua valendo:
Então, precisamos da integral de linha em . Vamos parametrizar usando coordenadas elípticas:
Lembra que a curva pertence ao plano .
Como temos uma volta completa no sentido horário, vai de a zero. Agora vamos derivar essa parametrização:
Agora vamos reescrever o campo em termos da parametrização:
Agora olha que coisa linda que vai acontecer:
Pra isso que servia o cilindro, pra simplificar o denominador do campo, percebeu? Agora vamos substituir tudo o que encontramos nessa fórmula aqui e finalmente calcular a integral de linha da primeira parte do campo em :
Passo 4
É, galera, não acabou, tem mais.
Para o campo
Temos o seguinte
Como esse campo não tem nenhuma singularidade, podemos escolher a superfície que quisermos para aplicar Stokes, de preferência uma que tenha só uma borda dessa vez né, por favor.
Vamos usar a parte de cima do paraboloide, pode ser? Só temos como fronteira então. Como a curva está orientada no sentido anti-horário, o vetor normal de aponta para cima.
Para parametrizar , vamos interpretá-la como a parte do paraboloide que está dentro do cilindro , pois essa é a projeção da borda de no plano . Assim, definimos como
Com domínio
Vamos então calcular o vetor normal a :
Então, temos:
Beleza, agora vamos calcular o rotacional desse campo:
Escrevendo em função da parametrização:
Agora vamos levar isso tudo para a fórmula:
Onde é o domínio da parametrização de :
Então vamos usar coordenadas elípticas:
E a região de integração passa a ser com . Levando isso para a integral:
Agora vamos resolver isso aí (sim, essa questão não acaba).
Usando a igualdade:
Temos:
Essa é a integral de linha em da segunda parte do campo.
Passo 5
Gente, finalmente, depois dessa saga, vamos chegar ao tão esperado resultado! Vamos somar os valores que encontramos para cada campo:
Se você chegou aqui realmente é guerreiro, está de parabéns, mesmo que não tenha acertado a questão. Essa era tensa mesmo, merecemos um break.