Teorema de Stokes
Calcule o trabalho realizado pelo campo ao longo de , onde
E é a curva dada pela interseção de com , orientada de forma que a projeção no plano é percorrida no sentido anti-horário.
Passo 1
Antes de tudo vamos fazer um gráfico da região para entender melhor a questão. Temos um cilindro elíptico cortado por um plano:
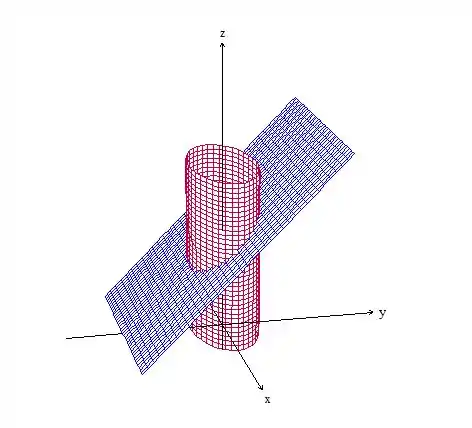
Esse desenho não precisa de precisão nenhuma, ok? É só para termos uma ideia mesmo, você pode desenhar um plano qualquer cortando o clilindro.
A questão pede para calcularmos a integral de linha em , que é a interseção do plano inclinado com o cilindro. Como podemos ver, forma uma elipse. Percebeu?
Passo 2
Ok, agora vamos analisar o problema. Reparou que a expressão do campo não é nem um pouco amigável, né? Imagina ainda substituir uma parametrização nisso aí, sem condições. Então vamos simplificar as coisas.
O Teorema de Stokes nos diz isso aqui:
Ou seja, podemos substituir essa integral de linha sobre a curva por uma integral do rotacional de sobre uma superfície que tenha a curva como fronteira. Ah, vamos usar o próprio retalho do plano em forma da elipse, né?
Agora vem o momento em que temos que tomar muito cuidado, olha a expressão do campo de novo:
Repare que e não podem ser iguais a zero, pois temos uma indeterminação, portanto, o campo não está definido no eixo .
Então, não podemos usar o plano como superfíce, na verdade, não podemos usar nenhuma superfície que tenha apenas como fronteira por causa disso!
Ferrou, né. Não, vamos usar uma superfície que tenha como uma de suas fronteiras. Em vez de usar o plano, vamos usar esse pedaço do cilindro, que também tem como fronteira.
Então, é o pedaço do cilindro cortado pelo plano e é a própria curva mais a borda debaixo do cilindro (outra elipse).Temos então:
Agora vamos pensar nas orientações. Se está no sentido anti-horário, pela Regra da Mão direita, deve ter vetor normal apontando para dentro. Consequentemente, gira no sentido horário.
Passo 3
Precisamos, então, calcular , sabendo que
Temos:
Passo 4
Agora precisamos parametrizar para encontrar seu vetor normal. Mas vamos pensar um pouco aqui, com malandragem.
Se a superfície é um cilindro com simetria em , seu vetor normal tem essa componente nula. Seria algo assim:
Agora, fazendo o produto escalar disso com olha o que encontramos:
Nem precisamos parametrizar nada aqui então, pois o resultado dessa integral é zero, viu?
Passo 5
Agora, para terminar a questão, precisamos calcular a integral de linha na outra borda da superfície, .
Como a elipse está no plano , sua equação é a mesma do cilindro elíptico:
Parametrizando isso aí em coordenadas elípticas, temos:
Como temos uma volta completa no sentido horário, vai de a .
Essa última componente é porque a curva está no plano .
Certo, agora vamos derivar isso aí:
Agora vamos escrever o campo nas variáveis da parametrização e usar a fórmula:
Levando para ai ntegral, temos:
Passo 6
Senta que agora começa o vudu. Vamos dividir o numerador e o denominador da integral da direita por :
Agora, vamos lembrar dessa igualdade:
Calma que tem mais..
Isso tudo para finalmente chegarmos nisso aqui, vamos reconhecer essa integral:
Comparando com a nossa integral, vemos que:
Logo
Passo 7
Temos então