Questão 2) Considere o campo vetorial
Mostre que
Com uma curva fechada dada pela interseção do cilindro com um gráfico de uma função positiva e diferenciável sobre o plano .
(Dica: Use Stokes duas vezes com superfícies apropriadas.)
Passo 1
Pois bem, teremos que provar que aquela integral de linha é igual a . Poxa, como o campo é bizarro, nada mais justo que pensarmos em utilizar o Teorema de Stokes para realizar essa prova:
Porém, não podemos aplicar essa igualdade de qualquer maneira, afinal temos que estar dentro das hipóteses do Teorema:
- Temos que ter uma curva fechada e delimitando uma superfície .
- Não podemos ter singularidades passando pela superfície.
- A curva e a superfície devem ter uma orientação positiva.
Então, percebendo que a curva é algo do tipo:
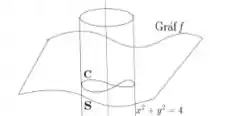
Afinal é a intersecção de um cilindro com uma função positiva . Infelizmente não podemos tomar como superfície o pedacinho da função que está dentro do cilindro, pois perceba que o campo possui singularidades em todo o eixo que corta essa superfície:
Então que superfície devemos pegar? Venha comigo no próximo passo !
Passo 2
Bem, Stokes não nos obriga a ter nenhum tipo de superfície específica, desde que a superfície escolhida possui como borda a curva está tudo certo. Então, uma superfície alternativa que podemos pegar é o próprio cilindro:
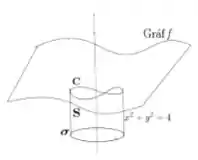
Afinal, ela circunda o eixo problemático, mas não tem nenhum ponto pertencente a esse eixo, saca?
Com esse cilindro, podemos aplicar o Teorema numa boa, adotando orientação positiva!
Mas veja que o cilindro não tem só a curva como borda , mas também a curva , ou seja:
Então:
Show, então no final das contas, para encontrar o resultado da integral de linha em , temos que calcular essas outras duas integrais do lado direito!
Passo 3
Vamos começar com a integral de linha:
Essa integral é uma integral em cima de uma curva circular no plano e no cilindro de raio :
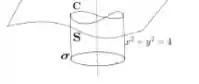
Então uma boa parametrização para ela é:
Só que quando substituirmos essa parametrização no campo ...
Vamos ganhar e outras expressões bizarras! Por isso, nós vamos seguir a dica do problema e aplicar novamente o Teorema de Stokes para tentar calcular essa integral de linha!
Só que agora, quem é a superfície ?
Passo 4
Bem, não pode ser o cilindro novamente, mas pode ser algum pedaço no próprio plano , afinal simplifica a vida neh?
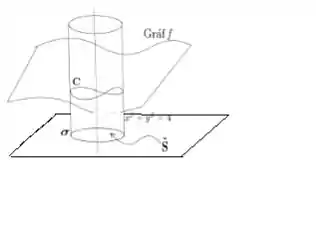
Só que esse pedaço de plano não pode passar pelo eixo , devido a singularidade, então a gente deve limitar a superfície por alguma outra curva fechada :
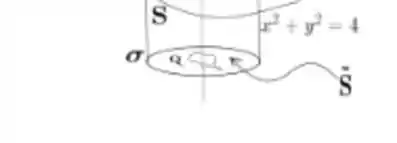
Só que essa curva não pode ser uma qualquer, neh? Tem que ser alguma curva que simplifique a vida! Olha para o campo novamente:
Seria muito interessante se tivéssemos ou constantes para simplificar o seno e ou o cosseno. Então o que acha de pegarmos um quadrado de lado ?
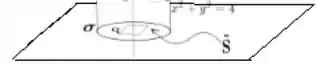
Esse quadrado é interessante, pois ele possui quatro retas que hora possui o e variando e hora é o contrário .
Então, pelo Teorema de Stokes, como a borda dessa superfície é a curva circular e essa curva :
Passo 5
Beleza, então resumindo os últimos passos, queremos provar que a integral de linha em cima de é , e no passo 2 vimos que:
No último passo, também vimos que:
Então, no final das contas teremos:
Agora é só calcular cada uma dessas integrais e ser feliz ! Vamos nessa?!
Passo 6
Vamos primeiro calcular as integrais duplas calculando o rotacional do campo :
Como...
Então, calculando as derivadas fáceis:
Essas duas são um pouco mais complicadas por ter que aplicar a regra da cadeia, mas da pra calcular:
E
Logo, como os dois rotacionais são iguais:
Então, as duas integrais de superfícies zeram!
Passo 7
Quanto a integral de linha em :
Temos que fazer com calma a integral em cada reta que compõe o quadrado!
Passo 8
Vamos começar com o lado e variando. Sua parametrização é:
O termo . E o campo
Logo:
Como
Passo 9
Agora, repetindo as contas para e variando (a reta de trás):
Termo . E o campo :
Então:
Como essa integral é a mesma da de cima só que ao invés de a gente colocar :
Passo 10
Agora, repetindo as contas para e variando (a reta de trás):
Termo . E o campo :
Então:
Passo 11
Por último, repetindo as contas para e variando (a reta de trás):
Termo . E o campo :
Então:
Passo 12
Logo:
Então, concluímos que:
Resposta
Prova pelo teorema de Stokes: