Questão 5) Sejam , (magnitude do vetor) e uma superfície fechada qualquer contendo a origem. Calcule
Passo 1
Antes de qualquer coisa vamos entender quem é essa função vetorial:
Então a função que vamos calcular a integral de superfície dela é...
Sacou?
Passo 2
Então queremos a integral de superfície dessa função vetorial em cima de que é uma superfície fechada qualquer que contenha a origem:
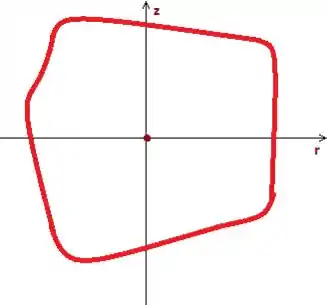
(Representa uma superfície fechada, só que seccionada pra você ver melhor ;)
Perceba que como não temos informação nenhuma sobre essa superfície (apenas que ela é uma qualquer) com certeza não vamos fazer essa questão pelo modo direto, pois precisaríamos dela. Por isso a ideia aqui é pensar em Gauss:
Agora, essa integral não pode ser aplicada assim... De qualquer maneira. Precisamos garantir as condições do Teorema que nos pede:
1º - Uma superfície fechada contendo o sólido no seu interior.
2º - Um campo sem singularidades onde estamos trabalhando.
3º - Vetores normais saindo do sólido.
Passo 3
A primeira exigência está sendo satisfeita, pois a superfície é fechada (maluca, mas fechada) e delimita um sólido no seu interior.
Já a segunda... Do campo não ter singularidades essa falha, pois veja:
Se você substituir o ponto , vai dar ruim a fração! Por isso o que Gauss faz? Vai lá e tira esse ponto problemático fora do sólido. Com o que? Com outra superfície:
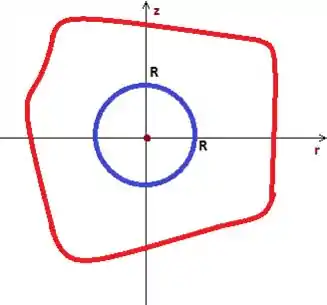
Em tese pode ser qualquer superfície, mas é melhor pegar uma esfera nesse caso, saca? Uma esfera que esteja dentro do sólido. Como não o conhecemos o sólido, vamos supor que uma esfera de raio conhecido cabe inteiramente dentro de :
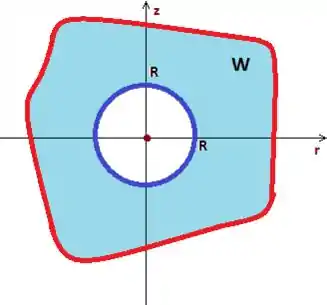
Passo 4
Show, só está faltando à condição de orientado positivamente, o que pra nossa alegria o problema não fala pra que direção ele quer o vetor normal na superfície bizarra , por isso vamos supor que sim, ele está saindo do sólido:
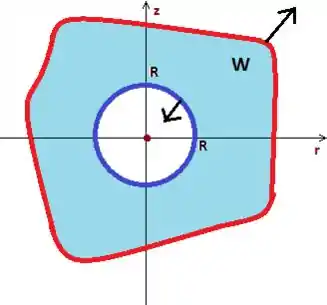
Passo 5
Aplicando o Teorema...
Mas veja aqui você que o teorema nos dá a igualdade, mas é válida só para integrais de superfície sobre a borda . Como a borda aqui é composta por duas, uma superfície e outra (esfera adicionada)...
Se queremos a integral sobre , a isolemos...
Podemos simplificar mais ainda se você inverter o sinal da integral em mas invertendo o sentido do vetor normal a ela, ou seja, ao invés de entrar, ele sai:
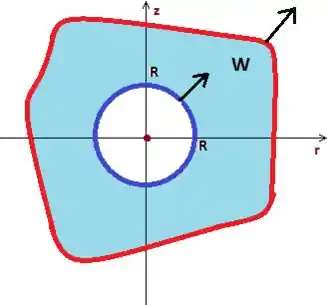
Passo 6
Vamos começar com a integral tripla, mas repare que ainda nos falta calcular o divergente:
Como
Calculando a primeira derivada parcial com atenção na regra da fração e na da cadeia...
Essa é só uma derivada, a da com relação à . Mas, como as demais são simétricas a ela encontramos por inspeção que...
Juntando todas elas em uma soma grandinha, então cuidado pra não errar nada...
HÁ! Essa conta imensa pra dar zero depois. Que ótimo não?
Passo 7
Calculando agora a integral de superfície sobre a esfera...
Precisamos primeiro parametrizar . Como é uma esfera:
Lembre-se que de que é o raio da esfera, um número e não uma variável. Então pela parametrização fica...
Onde e são...
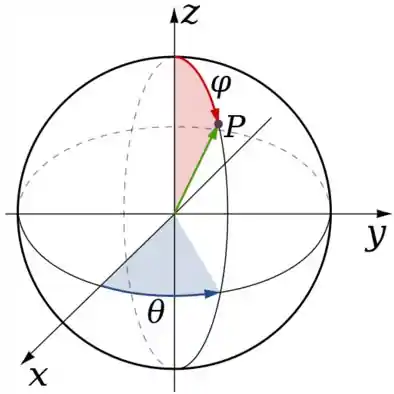
Logo, por comparação com a superfície ...
Passo 8
Devemos agora substituir os termos da parametrização na função
Lembre-se que pela equação da esfera, nem precisamos substituir o denominador, pois ...
Passo 9
Quanto ao termo que temos de encontrar, bem você pode jogar pela fórmula:
Onde
Ou, basta aplicar o bizu de vetor normal de superfícies esféricas:
Note que esse vetor satisfaz a condição de estar pra fora da esfera.
Passo 10
Retornando à integral de superfície:
E substituindo os caras:
Então pelo Teorema de Gauss...