Um sistema é composto de três componentes 1, 2 e 3, com confiabilidade 0,9; 0,8 e 0,7, respectivamente. O componente 1 é indispensável ao funcionamento do sistema; se 2 ou 3 não funcionam, o sistema funciona, mas com um rendimento inferior. A falha simultânea de 2 e 3 implica o não-funcionamento do sistema. Supondo que os componentes funcionem independentemente , calcular a confiabilidade do sistema.
Passo 1
Opa! Esse não tem desenho para interpretar... Mas tem o enunciado ué! Vamos reler com calma para entender o que ele falou:
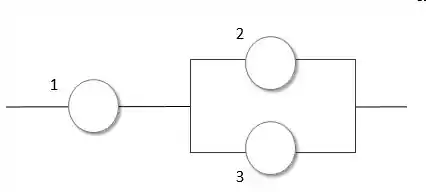
O componente 1 é indispensável, ou seja, ele precisa estar em série. Por que eu afirmo isso? Ué, relembra a teoria comigo:
- Em série: Precisam ambos funcionarem. Se um não funcionar o sistema não funciona.
- Em paralelo: Precisa de pelo menos um funcionando para o sistema funcionar.
Então o componente 1 precisa estar em série, pois ser indispensável significa que sem ele o sistema não consegue funcionar.
E os componentes 2 e 3? Bom, no enunciado diz que se um deles não funcionar não tem problema.. o sistema continua funcionando (com um rendimento inferior). Ou seja, eles estão em paralelo.
Depois o enunciado fala: A falha simultânea de 2 e 3 implica no não funcionamento do sistema Isso reafirma o fato de que 2 e 3, o conjunto, precisa estar em série com 1.
Vamos ver como fica o desenho:
Passo 2
Então vamos calcular agora!
- Componentes 2 e 3 (em paralelo)
Passo 3
- Componente 1 e Conjunto 23 (em série)
Resposta
0.846