O elemento infinitesimal abaixo está sujeito aos esforços mostrados. Determine quanto deve valer a tensão cisalhante para que a tensão em x seja o dobro da tensão em y quando o elemento estiver rotacionado de 45°no sentido anti-horário.
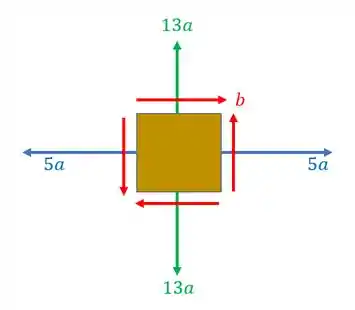
Passo 1
Aqui é importante entender o que está ocorrendo
Sabemos que devemos garantir que as tensões no estado transformado e no eixo x sejam iguais ao dobro das tensões no eixo y, como sabemos que as fórmulas são
Basta fazermos a igualdade que foi mencionada afim de que essas tensões sejam iguais, para isso faremos
Isolando tudo em um lado teremos que
Isolando as tensões teremos que
Com isso teremos que a fórmula será
Passo 2
Agora que já temos a nossa fórmula basta que substituamos os valores, com isso teremos que
Vamos substituir na equação que encontramos antes
Logo teremos que
Agora vamos testar para ver se de fato fizemos correto.
Passo 3
Usando a nossa fórmula teremos que
Se achamos que a tensão em x é de , sabemos que para estar correto a tensão em y deverá ser de , vamos testar então
Logo de fato a conta que fizemos está correta, como o objetivo era determinar o valor do cisalhante, teremos que o nosso cisalhante deverá valer
Para que a nossa tensão no eixo x seja o dobro da tensão no eixo y quando girarmos o nosso elemento em 45° no sentido anti-horário.