Ângulo Entre Dois Vetores
Produzido por Bruno PestanaTeoria
Fala aí, seja bem vindo ao Responde Aí! Bora aprender como calcular o ângulo entre dois vetores?!
Como Calcular o Ângulo entre Dois Vetores
Se eu te pedisse pra calcular o ângulo
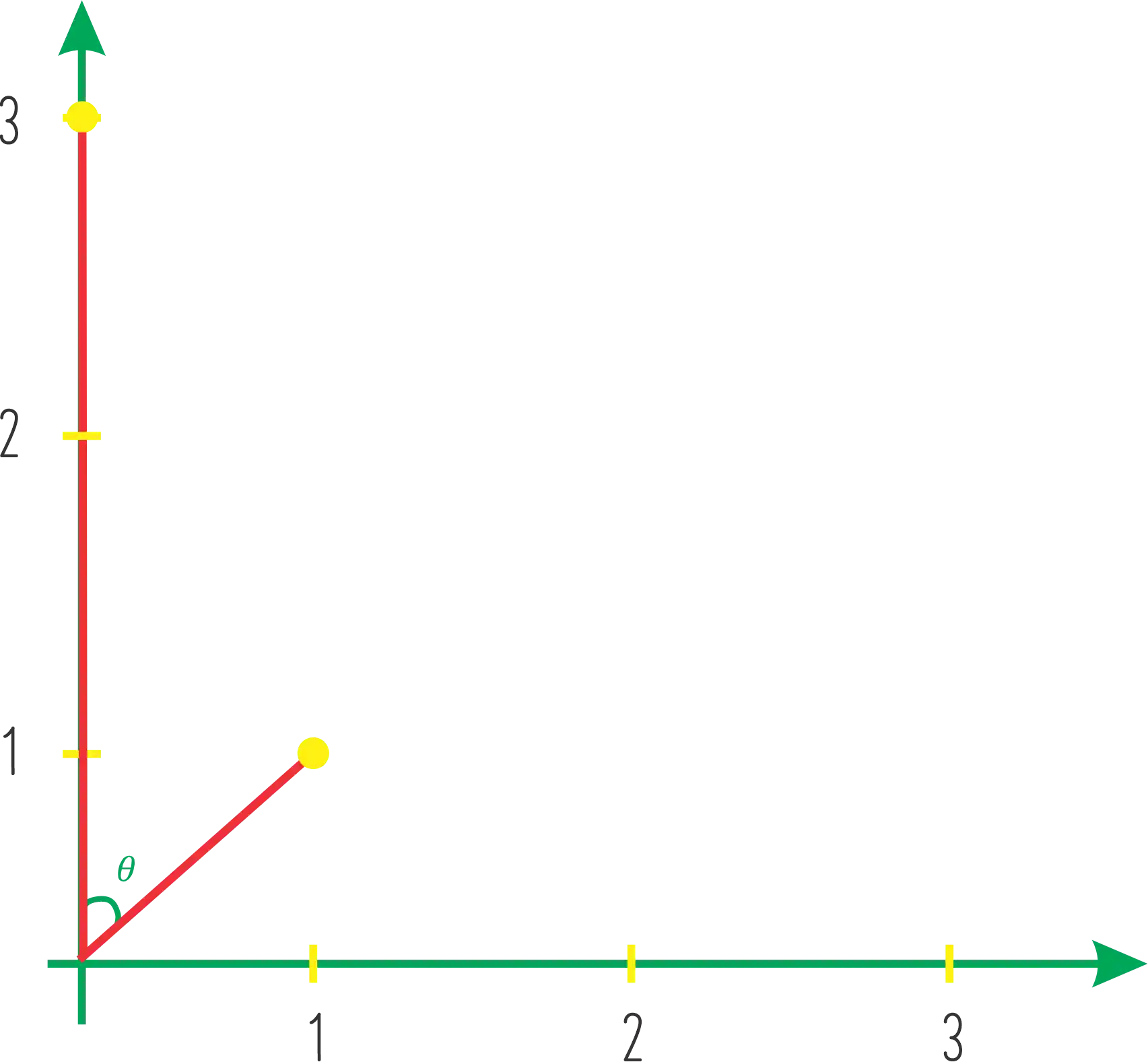
Pra isso a gente vai usar essa formulinha aqui:

Ou então podemos calcular o cosseno de
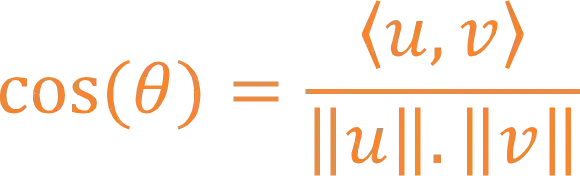
Esse $
Agora vamos ver na prática como a gente calcula esse
Substituindo os nossos dados na fórmula:
Calculando, temos:
E finalmente:
Você também pode conferir esse conteúdo em vídeo! 👇
Vetores Ortogonais
Vetores ortogonais são vetores perpendiculares, ou seja eles forma um ângulo de 90° entre eles! Nesse caso é importante reparar que o pro produto interno entre eles será igual a zero. Por exemplo, vamos verificar os vetores
Formalmente a gente tem o seguinte teorema:
Teorema:
Para
Isso acontece porque para
Vetores Ortonormais
Agora que sabemos o que significa um conjunto de vetores serem ortogonais, podemos definir também um conjunto de vetores ortonormais! Quando temos um conjunto de vetores ortonormais isso quer dizer que esses vetores são ortogonais entre si e todos eles são unitários.

Observe agora os conjuntos de vetores
Repare que o produto interno desses vetores dá
Agora vamos praticar com exercícios?