Questão 1: Seja a curva regular dada pela interseção das superfícies
- Faça um esboço das superfícies e da curva .
- Descreva uma parametrização regular de .
- Calcule a integral de linha
- Calcule a integral de linha
Onde e está orientada saindo do ponto .
Passo 1
Item a)
Para desenhar essa curva no espaço, devemos desenharas superfícies do problema. A curva vai estar na intersecção delas !
Vamos começar com a primeira superfície da noite:
Ora, é uma parábola no plano :
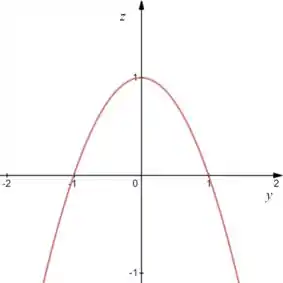
Como essa equação independe de , então significa que devemos “puxar” a parábola ao longo do eixo :
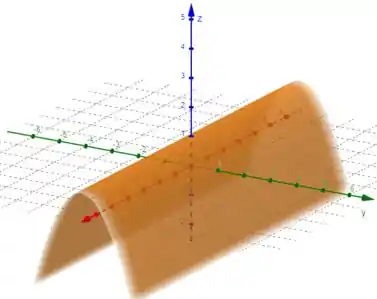
Para desenhar essa última superfície, , podemos fazer algo semelhante:
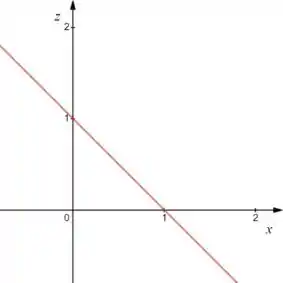
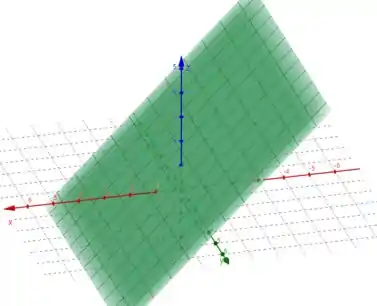
Veja a nossa curva ali no meio das superfícies!
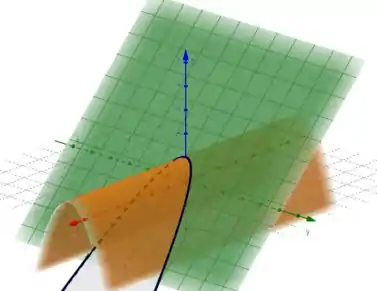
Passo 2
Item b)
Uma boa parametrização para essa curva é utilizando a parametrização explícita, onde podemos considerar o como o parâmetro . Assim ganhamos o em função desse parâmetro:
E também o :
Logo, uma boa parametrização é:
Para descobrir os limites de , devemos recordar a seguinte restrição:
Logo:
Passo 3
Vamos verificar se essa parametrização é regular ou não. Para isso, temos que verificar se nesse intervalo:
Veja que por causa dessa coordenada , esse nunca se anula, então sim! É regular:
Passo 4
Item c)
Beleza, então vamos calcular essa integral de linha:
Para isso devemos seguir o passo a passo a seguir:
- Parametrizar a curva:
- Calcular o termo :
- Substituir os termos da parametrização:
Calculando por uma mudança de variável:
Trocando também os limites:
Passo 5
Item d)
Por propriedade de campos conservativos tal que possui uma função potencial :
Onde é o ponto final da curva, enquanto que é o ponto inicial. Como na nossa curva os pontos extremos são:
E
De acordo com o enunciado, temos uma orientação tal que a curva sai de , logo ele é o ponto inicial:
Então:
Como ...
Resposta
Letra a)
Letra b)
Letra c)
Letra d)