Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Função Potencial

Ver Teoria
Exercício 105123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 5) Seja F → x ,   y = a x 2 y + y 3 + e x + 1 ,   2 x 3 + b x y 2 + e y + 2

  1. Para que valores de a e b o campo vetorial F → é conservativo?
  2. Para os valores encontrados no item 1 , determine um potencial f de F → tal que f 0 ,   0 = 2018 .
  3. Seja a = 5 , b = 4 . Determinar

∫ C   F → ⋅ d r →

Onde C é a curva parametrizada por r → t = cos ⁡ t , sin ⁡ t ,   t ∈ 0 ,   2 π .

Passo 1

a )

Ouvi conservativo??? Então a primeiríssima coisa que você tem que ver é se o campo funciona em todos os pontos do espaço. Em outras palavras, é verificar se ele é simplesmente conexo!

Pow! Olha para o nosso campo

F → x ,   y = a x 2 y + y 3 + e x + 1 ,   2 x 3 + b x y 2 + e y + 2

Repare bem que ele é composto por polinômios e por exponenciais, ou seja, funciona pra qualquer ponto que a gente quiser! Sacou? Então ele é simplesmente conexo sim!

Mas a análise não acabou por aqui, neh? Bora para o último quesito...

Passo 2

Para o campo ser conservativo também, outra coisa que precisa acontecer é essa parada aqui ser verdadeira

∂ F 2 ∂ x - ∂ F 1 ∂ y = 0

OBS: Esse termo do primeiro membro é aquela famosa subtração que utilizamos no Teorema de Green, se lembra? F 1 e F 2 são as componentes do campo...

F → x ,   y = F 1 ,   F 2 = a x 2 y + y 3 + e x + 1 ,   2 x 3 + b x y 2 + e y + 2

Derivando...

∂ F 2 ∂ x = ∂ ∂ x 2 x 3 + b x y 2 + e y + 2 = 6 x 2 + b y 2

∂ F 1 ∂ y = ∂ ∂ y a x 2 y + y 3 + e x + 1 = a x 2 + 3 y 2

Substituindo...

∂ F 2 ∂ x - ∂ F 1 ∂ y = 0                 →                       ∂ F 2 ∂ x - ∂ F 1 ∂ y =

6 x 2 + b y 2 - a x 2 - 3 y 2 = 0

Pow, veja que se a = 6 e b = 3 , não importa o valor de x e y que o resultado sempre é 0 , tornando o campo conservativo!

F → x ,   y = 6 x 2 y + y 3 + e x + 1 ,   2 x 3 + 3   x y 2 + e y + 2

Passo 3

b )

Tá! Ele é conservativo, mas o que isso significa exatamente?

Significa que o campo possui uma função potencial f x ,   y   que, por definição, atende a equação:

F → = ∇ f

Esse segundo termo, se você não se recorda, é a gradiente da função ômega definido como sendo o vetor de derivadas parciais...

∇ f = ∂ f ∂ x , ∂ f ∂ y

Pela igualdade de função vetorial então temos que...

F → = ∇ f           →                 6 x 2 y + y 3 + e x + 1 ,   2 x 3 + 3   x y 2 + e y + 2 = ∂ f ∂ x , ∂ f ∂ y

Por igualdade de vetor...

1 º )                   ∂ f ∂ x = 6 x 2 y + y 3 + e x + 1

      2 º )                   ∂ f ∂ y = 2 x 3 + 3   x y 2 + e y + 2

O que vamos fazer aqui agora, basicamente é ressorver essas equações diferenciais e tirar o valor de f (a função potencial )

Passo 4

Da primeira equação diferencial...

1 º )                   ∂ f ∂ x = 6 x 2 y + y 3 + e x + 1

Podemos, grosso modo, “passar” o d x pra lado de lá e integrar dos dois lados...

  ∂ f = 6 x 2 y + y 3 + e x + 1 ∂ x

Integrando...

∫     d f = ∫     6 x 2 y + y 3 + e x + 1 d x →

f = ∫     6 x 2 y + y 3 + e x + 1 d x →

Integrando com relação a x agora (tome y sendo uma constante)...

f = 6 y ⋅ x 3 3 + y 3 ⋅ x + e x + x + C y   →

f = 2 y x 3 + x y 3 + e x + x + C y

Veja que aparece um C ( y ) ! Você pode pensar nela como uma constante de integração, mas como integramos em x e a função tem outra variável, a “constante” passa a depender dessa outra variável, saca? Se você ainda não estiver convencido, derive esse ômega com relação à x ! Você vai reparar que a C y some por depender somente de y !

Passo 5

Beleza, mas agora vamos resolver a segunda equação de modo análogo...

      2 º )                   ∂ f ∂ y = 2 x 3 + 3   x y 2 + e y + 2         →

∂ f = 2 x 3 + 3   x y 2 + e y + 2 ∂ y     →

∫     d f = ∫     2 x 3 + 3   x y 2 + e y + 2 d y   →

(Agora, para integrar em y tome x como uma constante):

f = 2 x 3 ⋅ y + 3 x ⋅ y 3 3 + e y + 2 y + C x   →

f = 2 x 3 y + x y 3 + e y + 2 y + C x

Agora apareceu C x pelo mesmo motivo de C y ali em cima.

Passo 6

Veja que nos dois últimos passos, encontramos duas funções diferentes...

1 º )                     f = 2 y x 3 + x y 3 + e x + x + C y    

2 º )                     f = 2 x 3 y + x y 3 + e y + 2 y + C x

A resposta verdadeira vai ser uma combinação das duas da seguinte forma:

  1. Toda termo igual, aparece uma só vez...

    2. f = 2 y x 3 + x y 3 …

  2. Todo termo diferente aparece também...

    3. f = 2 y x 3 + x y 3 + e x + x + e y + 2 y …

  3. As funções C x e C y não coloca, mas no lugar dela, coloca uma constante k ...

f = 2 y x 3 + x y 3 + e x + x + e y + 2 y + k

Basicamente a gente já acabou, pois encontrou todas as funções potenciais de f . Aí você poderia perguntar: “Todas?! Mas eu só vejo uma ”. Bem, repare que k é uma constante e pode valer qualquer número real. Pra cada um eu tenho uma resposta diferente, saca?

Nesse caso, tem como de descobrir k , pois o problema disse que

f 0 ,   0 = 2018   →

f = 2 y x 3 + x y 3 + e x + x + e y + 2 y + k         →  

f 0 ,   0 = 0 + 0 + e 0 + 0 + e 0 + 0 + k = 2018       →

2 + k = 2018       →             k = 2016

Logo, a função potencial pedida é...

f x ,   y = 2 y x 3 + x y 3 + e x + x + e y + 2 y + 2016

Passo 7

c )

Queremos agora calcular uma integral de linha

∫ C   F → ⋅ d r →

Onde o campo F → não é mais o anterior, pois a = 5 e b = 4 são diferentes, logo o campo F → será...

F → x ,   y = 5 x 2 y + y 3 + e x + 1 ,   2 x 3 + 4 x y 2 + e y + 2

Isso é uma pena, pois esse campo não é conservativo já que mudou o a e o b ! Mas como ele deu a curva C já parametrizada

r → t = cos ⁡ t , sin ⁡ t ,   t ∈ 0 ,   2 π

Podemos simplesmente substituir que a solução vai vir rápida, correto?

ERRADO! Poxa, o problema não ia ser tão bonzinho assim com a gente, neh? Veja que o campo tem exponencial e quando substituir os termos x e y pelos da parametrização, iam aparecer coisas bizarras como exponencial de seno...

e y = e sin ⁡ t

Por isso, a ideia vai ser tentar escapar para o teorema de Green:

∫ C   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A

Passo 8

Pow, mas antes vamos calcular aquela subtração do teorema pra ver se vai valer a pena mesmo, neh, pois não queremos fazer conta à toa. Mas atenção, você poderia se confundir e falar que essa subtração é 0 , como vimos no passo 2, mas lembre-se que os campos são diferentes!!!

Sem mais delongas, bora pra conta...

F → x ,   y = F 1 ,   F 2 = 5 x 2 y + y 3 + e x + 1 ,   2 x 3 + 4 x y 2 + e y + 2

∂ F 2 ∂ x = ∂ ∂ x 2 x 3 + 4 x y 2 + e y + 2 = 6 x 2 + 4 y 2

∂ F 1 ∂ y = ∂ ∂ y 5 x 2 y + y 3 + e x + 1 = 5 x 2 + 3 y 2

Subtraindo...

∂ F 2 ∂ x - ∂ F 1 ∂ y = 6 x 2 + 4 y 2 - 5 x 2 - 3 y 2 =

x 2 + y 2

Bem, esse termo simplifica muito, então vamos sim utilizar Green !

Passo 9

Show! Mas para aplicar o teorema, temos antes que verificar as condições que ele nos exige:

  1. Uma curva C fechada delimitando a região D .
  2. A curva tem que estar orientada positivamente (girando no sentido anti-horário).
  3. Campo F → sem singularidades.

Verificando...

Em 1 ) Sim, a curva é fechada! Pois se você perceber, a parametrização dela

r → t = cos ⁡ t , sin ⁡ t ,   t ∈ 0 ,   2 π

É de uma circunferência de raio 1 e centrada na origem:

Em 2) O problema não nos fala nada quanto a orientação, onde a gente pode assumir que sim, a curva gira no sentido anti-horário:

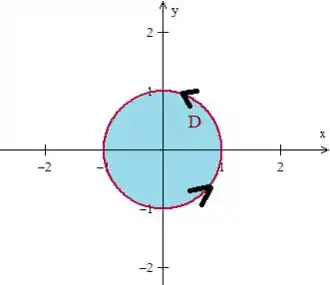
Em 3) Já vimos que o campo não tem problemas em nenhum ponto, ou seja, ele não tem singularidades.

Passo 10

Ok! Com as condições sendo satisfeitas, podemos utilizar o teorema de Green para calcular a integral de linha...

∫ C   F → ⋅ d r → = ∬ D   ∂ F 2 ∂ x - ∂ F 1 ∂ y d A =

∬ D   x 2 + y 2   d A

Passo 11

Para resolver a integral dupla dentro de um círculo, ora, mudança de coordenadas para as polares:

x = r cos ⁡ θ

y = r sin ⁡ θ

J = r

x 2 + y 2 = r 2

Não podemos deixar de lado os limites de r e θ , neh? Bem, mas isso é tranquilo olhando para o círculo novamente:

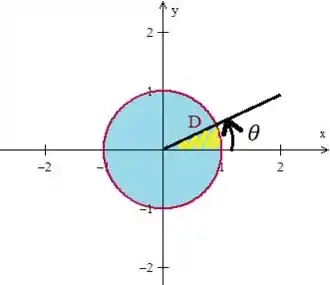
Veja que θ tem que dar uma volta completa:

0 ≤ θ ≤ 2 π

Enquanto o raio varia da origem até o raio máximo que é...

0 ≤ r ≤ 1

Show, gora é só trocar a integral dupla, não se esquecendo de multiplicar a função do integrando pelo Jacobiano...

∬ D   x 2 + y 2   d A = ∫ 0 2 π ∫ 0 1 r 2 ⋅ J   d r d θ =

∫ 0 2 π ∫ 0 1 r 3   d r d θ

Passo 12

Por fim é só matar a integral...

∫ 0 2 π ∫ 0 1 r 3   d r d θ = ∫ 0 2 π r 4 4 0 1 d θ =

∫ 0 2 π 1 4 d θ = 1 4   θ   0 2 π =

2 π 4 = π 2

Onde pelo teorema de Green, esse é o valor de integral de linha...

∫ C   F → ⋅ d r → = π 2

Resposta

a )         a = 6     e       b = 3

b )     f x ,   y = 2 y x 3 + x y 3 + e x + x + e y + 2 y + 2016

c )     π 2

Exercícios de Livros Relacionados

6. Mostre que as integrais ∮ C F 1 x , y d x + F 2 x , y d y São nulas, quais quer que sejam os contornos fechados C contidos no domínio F 1,F 2 , onde F 1 x , y = sen ⁡ x + 4 x y F 2 x , y = 2 x 2 -
Um escoamento é representado pelo campo de velocidade v → = y 2 + z 2 i → + x z j → + 2 x 2 y 2 k → Verificar se o escoamento é:b) irrotacional.
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?f) f → x , y , = x 2 + y , y 2 - x , em R 2
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?g) f → x , y , z = - sen ⁡ x + cos ⁡ x , z , y em R 3
Usando o teorema 6.9 . 3 , o que se pode afirmar sobre o campo vetorial dado?h) f → x , y , = sen ⁡ x , cos ⁡ y , em R 2