Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Quádricas com Rotação

Ver Todos os Exercícios

Teoria

Já vimos cônicas com rotação, mas e as Quádricas???

Vamos te explicar direitinho agora. Mas já adianto que é bem parecido com o que fizemos para as cônicas!

Também já vimos que no espaço, ou seja, no R ³ , as quádricas são superfícies definidas por equações do tipo :

A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + G x + H y + I z + J = 0

Daí temos os óides: parabolóides, elipsoides e por ai vai.

Se você pegou a ideia não é difícil estender o conceito para o R 4 , R 5 e o R 24153 mas felizmente nós vamos nos ater a dimensões mais amigáveis.

Mas galera, se vocês ficam com essa cara aqui:

Quando vêem uma equação desse tamanho:

A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + G x + H y + I z + J = 0

Saiba que é completamente normal e os matemáticos também se sentem assim. Por isso, vamos aprender a domar isso ai pra aparecer uma coisa mais mansa. Dá uma olhada como fazemos.

Quádricas com rotação

A ideia de todas as contas que vamos fazer é achar um novo sistema de coordenadas legal pra gente poder olhar a quádrica. A equação só tá feia porque estamos olhando por um sistema de coordenadas ruim, mas se escolhermos um novo de forma que fique tipo assim:

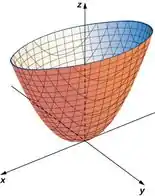
As coisas vão ficar show de bolinhas!

O que fazemos é pegar uma quádrica rotacionada e, provavelmente, transladada e achar um novo eixo de coordendas “desrotacionado” e “destransladado”. No final das contas você vai sacar do que eu to falando!

Cara vou ser direto com você: nosso objetivo aqui é pegar

A x 2 + B y 2 + C z 2 + D x y + E x z + F y z + G x + H y + I z + J = 0

E transformar em algo desse tipo

A ' x 2 + B ' y 2 + C ' z 2 + K = 0

Pra vocês sacarem como tudo funciona, nós vamos trabalhar tentando simplificar uma quádrica aqui:

2 x 2 + 2 y 2 + z 2 + 2 x z + 2 y z + 2 x - 2 y + 6 z + 14 = 0

Primeiro, vamos escrever isso aí na forma matricial, ou seja:

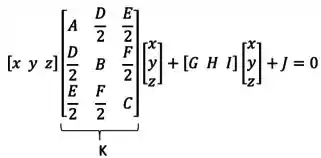
Substituindo tudo, ficamos com:

x     y     z 2 0 1 0 2 1 1 1 1 x y z + 2   - 2     6 x y z + 14 = 0

Onde   K = 2 0 1 0 2 1 1 1 1

Agora, partiu calcular os Autovalores   ( λ ) !

Se você não lembra a formulinha, é essa aqui ô: K - λ I = 0

Substituindo os valores,

K - λ I = 2 - λ 0 1 0 2 - λ 1 1 1 1 - λ = 0

Calculando esse determinante, achamos:

2 - λ 2 - λ 1 - λ - 2 - λ + 2 - λ = 0

λ λ 2 - 5 λ + 6 = 0

Logo, λ 1 = 0 ,   λ 2 = 3 ,   λ 3 = 2

Partiu calcular os Autovetores agora!

A formulinha é K - λ I v = 0

Para λ 1 = 0 , temos:

2 0 1 0 2 1 1 1 1 x y z = 0 0 0

2 x + z = 0 2 y + z = 0 ⇒ y = x z = - 2 x

Podemos escolher qualquer valor para x ,   y ou z desde de eles satisfaçam a relação aí de cima!

Vou escolher x = 1 . Logo, z = - 2   e y = 1

Com isso, achamos o vetor ( 1 ,   1 ,   - 2 ) ! Mas não esquece que o vetor precisa ser unitário, então vamos dividir pela norma!

E achamos o autovetor v 1 = ( 6 6 , 6 6 , - 2 6 6 )

Para λ 2 = 3

- 1 0 1 0 - 1 1 0 1 - 2 x y z = 0 0 0

- x + z = 0 - y + z = 0 ⇒ x = z y = z

Se x = 1 , então y = z = 1

Logo o autovetor é v 2 = ( 3 3 , 3 3 , 3 3 )

Para λ 3 = 2

0 0 1 0 0 1 1 1 - 1 x y z = 0 0 0

z = 0 x + y - z = 0 ⇒ z = 0 x = - y

Se x = 1 , então z = 0 e y = - 1

Logo o autovetor é v 3 = ( 2 2 , - 2 2 , 0 ) .

Com isso, conseguimos montar nossa matriz dos autovalores ( M ) e dos autovetores ( N ) e substituir em uma nova fórmula matricial:

x '     y '     z ' M x ' y ' z ' + G     H     I N x ' y ' z ' + J = 0

Sendo M = λ 1 0 0 0 λ 2 0 0 0 λ 3 e N = ↑ ↑ ↑ v 1 v 2 v 3 ↓ ↓ ↓

CUIDADO: A ordem dos autovalores e autovetores importa, então cuidado para não trocar eles!!

Substituindo os valores:

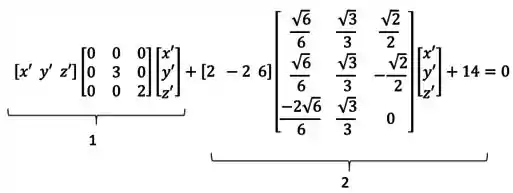
Nessa nova fórmula, o que fizemos foi eliminar a rotação criando outros eixos coordenados x ' ,   y ' ,   z ' .

Bem, agora precisamos sair da forma matricial.

Resolvendo a parte 1, ficamos com:

λ 1 x ' 2 + λ 2 y ' 2 + λ 3 z ' 2

3 y ' 2 + 2 z ' 2

Resolvendo a parte 2:

A relação entre x y z e x ' y ' z ' é:

x y z = N x ' y ' z '

Então:

2 x - 2 y + 6 z = 2 - 2 6 6 6 3 3 2 2 6 6 3 3 - 2 2 - 2 6 6 3 3 0 x ' y ' z '

2 x - 2 y + 6 z = - 2 6 2 3 2 2 x ' y ' z ' = - 2 6 x ' + 2 3 y ' + 2 2 z '

Ufa! A equação depois disso tudo ficou:

3 y 2 + 2 z 2 - 2 6 x + 2 3 y + 2 2 z + 14 = 0

Aqui nós pegamos um caso meio atípico, não poderemos eliminar todos os termos lineares como podemos na maioria das vezes. Peguei esse exemplo só pra vocês não se assustarem se isso acontecer depois.

Ainda falta uma coisinha só!

Eu sei que é longo, mas daqui a pouco você se acostuma!

Fizemos isso tudo para “desrotacionar” a quádrica, mas ela pode estar transladada também! Reparem que nesse caso ela está transladada, porque os termos não estão bonitinhos ainda, ou seja, não conseguiríamos identificar essa quádrica do jeito que ela tá.

Para resolver essa marimba é só completarmos os quadrados (lembra lá do Ensino Médio) pra tirar os termos lineares que conseguirmos:

3 y 2 + 2 3 y + 1 + ( 2 z 2 + 2 2 z + 1 ) - 2 6 x + 14 = 2

3 y + 1 2 + 2 z + 1 2 - 2 6 x + 12 = 0

3 y 2 + 1 3 2 + 2 z 2 + 1 2 2 - 2 6 x 2 + 12 = 0

Fazendo agora:

x 3 = x 2

y 3 = y 2 + 1 3

z 3 = z 2 + 1 2

A equação da quádrica finalmente chega em:

3 y 2 + 2 z 2 - 2 6 x + 12 = 0

Bem mais simples essa equação aí, né.

Agora sim, haha. Olha como é a cara dela:

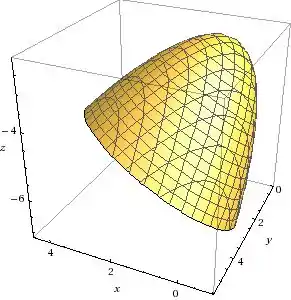
O que fizemos no fim das contas é achar um sistema de coordenadas mais adequado pra olhar ela. O lance de não conseguirmos eliminar o termo linear de x   é porque trata-se de um paraboloide, figura que não tem centro geométrico.

Eu tenho certeza que você deve estar meio assustado com todas essas contas, mas se acalme ai. A gente pegou aqui o caso mais completo de exercício, em geral eles vão te pedir só pedaços do que fizemos aqui agora, mas se você entender esse aqui, vai conseguir fazer todos molinho. Bora lá pra você ver.

Exercícios Resolvidos

Exercício Resolvido #1

P3 USP 2016

Passo 1

Sem segredos no enunciado, temos uma quádrica e sua matriz, que possui autovalores 2 e 4 . Temos que achar sua equação simplficada

Passo 2

Ora, o enunciado já fez quase todo o trabalho para nós. Tendo os autovalores da matriz, vimos que eles são os coeficientes dos termos quadráticos da equação simplificada, então estamos procurando uma equação onde os coeficientes são 4 e 2 , que no caso é:

4 u 2 + 2 v 2 = 1

Resposta

e   4 u 2 + 2 v 2 = 1

Exercício Resolvido #2

Callioli, C.A; Domingues, H.H. e Costa, R.C.F., Álgebra Linear e Aplicações, 4a. edição, São Paulo, Atual, 1983.

Ache a equação canônica de:

x 2 + 4 x y - 2 y 2 = 6

Passo 1

Aqui queremos achar a equação da quádrica numa base em que não apareça o termo misto, pra isso só precisamos calcular os autovalores da matriz associada.

Passo 2

Temos que:

q C a n = 1 2 2 - 2

Calculando os autovalores:

det ⁡ q C a n - λ I = 0 ⇒ 1 - λ 2 2 - 2 - λ = 0

- 1 - λ 2 + λ - 4 = 0

λ 2 + λ - 6 = 0

Logo os autovalores são - 3 e 2.

Assim uma equação reduzida da quádrica é:

- 3 x 2 + 2 y 2 = 6

Resposta

- 3 x 2 + 2 y 2 = 6

Exercício Resolvido #3

Callioli, C.A; Domingues, H.H. e Costa, R.C.F., Álgebra Linear e Aplicações, 4a. edição, São Paulo, Atual, 1983.

Ache a equação canônica de:

3 x 2 + 2 x y + 3 y 2 = 1

Passo 1

Aqui queremos achar a equação da quádrica numa base em que não apareça o termo misto, pra isso só precisamos calcular os autovalores da matriz associada.

Passo 2

Temos que:

q C a n = 3 1 1 3

Calculando os autovalores:

det ⁡ q C a n - λ I = 0 ⇒ 3 - λ 1 1 3 - λ = 0

3 - λ 2 - 1 = 0

λ 2 - 6 λ + 8 = 0

Logo os autovalores são 4   e 2.

Assim uma equação reduzida da quádrica é:

4 x 2 + 2 y 2 = 1

Resposta

4 x 2 + 2 y 2 = 1

Exercício Resolvido #4

Callioli, C.A; Domingues, H.H. e Costa, R.C.F., Álgebra Linear e Aplicações, 4a. edição, São Paulo, Atual, 1983.

Ache a equação canônica de:

x 2 + x y - y 2 + z 2 + 2 y z

Passo 1

Aqui queremos achar a equação da quádrica numa base em que não apareçam os termos mistos, pra isso só precisamos calcular os autovalores da matriz associada.

Passo 2

Temos que:

q C a n = 1 1 2 0 1 2 - 1 1 0 1 1

Calculando os autovalores:

det ⁡ q C a n - λ I = 0 ⇒ 1 - λ 1 2 0 1 2 - 1 - λ 1 0 1 1 - λ = 0

- 1 - λ 2 1 + λ - 1 - λ - 1 4 1 - λ = 0

1 - λ λ 2 - 1 - 5 4 = 0

1 - λ λ - 3 2 λ + 3 2 = 0

Logo os autovalores são 1 , 3 2 e - 3 2 .

Assim uma equação reduzida da quádrica é:

x 2 + 3 2 y 2 - 3 2 z 2 = 1

Resposta

x 2 + 3 2 y 2 - 3 2 z 2 = 1

Exercício Resolvido #5

Callioli, C.A; Domingues, H.H. e Costa, R.C.F., Álgebra Linear e Aplicações, 4a. edição, São Paulo, Atual, 1983.

Ache a equação canônica de:

11 x 2 + 10 y 2 + 6 z 2 - 12 x y - 8 y z + 4 x z - 12 = 0

Passo 1

Aqui queremos achar a equação da quádrica numa base em que não apareçam os termos mistos, pra isso só precisamos calcular os autovalores da matriz associada.

Passo 2

Temos que:

q C a n = 1 1 - 6 2 - 6 10 - 4 2 - 4 6

Calculando os autovalores:

det ⁡ q C a n - λ I = 0 ⇒ 11 - λ - 6 2 - 6 10 - λ - 4 2 - 4 6 - λ = 0

- λ 3 + 27 λ 2 - 180 λ + 324 = 0

As soluções desta equação polinomial são:

λ 1 = 3 ,   λ 2 = 6   e λ 3 = 18

Assim uma equação reduzida da quádrica é:

3 x 2 + 6 y 2 + 18 z 2 = 12

Resposta

3 x 2 + 6 y 2 + 18 z 2 = 12

Exercício Resolvido #6

BOLDRINI, Luis José e outros. Álgebra Linear. 3 ed. São Paulo: Harbra, 1986.

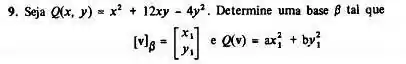
Passo 1

Agora temos que achar o sistema de coordenadas no qual a forma quadrática (dá no mesmo que se fosse formalmente uma quádrica) fica reduzida. Pra isso, como vimos na teoria, temos só que calcular os autovetores da matriz associada

Passo 2

Temos que:

q C a n = 1 6 6 - 4

Calculando os autovalores:

det ⁡ q C a n - λ I = 0 ⇒ 1 - λ 6 6 - 4 - λ = 0

- 1 - λ 4 + λ - 36 = 0

Logo os autovalores são - 8 e 5 .

λ = - 8

9 6 6 4 x y = 0 0

6 x + 4 y = 0 ⇒ y = - 3 x 2

x 2 + 9 x 2 4 = 1 ⇒ x = 2 13 13

Logo o autovetor de norma 1   associado é 2 13 13 , - 3 13 13

λ = 5

- 4 6 6 - 9 x y = 0 0

- 4 x + 6 y = 0 ⇒ y = 2 x 3

x 2 + 4 x 2 9 = 1 ⇒ x = 3 13 13

Logo o autovetor de norma 1   associado é 3 13 13 , 2 13 13

Como a base que procuramos é justamente aquela formada pelos autovetores:

β = 2 13 13 , - 3 13 13 , 3 13 13 , 2 13 13

Resposta

β = 2 13 13 , - 3 13 13 , 3 13 13 , 2 13 13

Exercício Resolvido #7

Callioli, C.A; Domingues, H.H. e Costa, R.C.F., Álgebra Linear e Aplicações, 4a. edição, São Paulo, Atual, 1983.

Ache a equação canônica de:

3 x 2 + 2 y 2 - 3 z 2 + 5 y z = 1

E indique a substituição linear utilizada.

Passo 1

Aqui queremos achar a equação da quádrica numa base em que não apareçam os termos mistos,e além disso dizer como as variáveis x 2 , y 2 e z 2 se relacionam com x 1 , y 1   e z 1 . Pra isso precisamos achar a base para a qual passamos quando fazemos a diagonalização da matriz.

Passo 2

Temos que:

q C a n = 3 0 0 0 2 5 2 0 5 2 - 3

Calculando os autovalores:

det ⁡ q C a n - λ I = 3 - λ 0 0 0 2 - λ 5 2 0 5 2 - 3 - λ = 0

- 3 - λ 2 - λ 3 + λ - 25 4 3 - λ = 0

3 - λ λ 2 + λ - 6 - 25 4 = 0

3 - λ λ + 1 - 5 2 2 λ + 1 + 5 2 2 = 0

Logo uma equação reduzida é:

3 x 2 + 5 2 - 1 2 y 2 - 5 2 + 1 2 z 2 = 1

Passo 3

-

Agora os autovetores:

λ = 3

0 0 0 0 - 1 5 2 0 5 2 - 6 x y z = 0 0 0

- y + 5 2 z = 0 5 2 y - 6 z = 0 ⇒ y = 0 z = 0

x 2 = 1 ⇒ x = 1

Logo o autovetor de norma 1 correspondente é e 1 = ( 1,0 , 0 )

λ = 5 2 - 1 2

- 5 2 + 7 2 0 0 0 5 1 - 2 2 5 2 0 5 2 5 - 1 - 2 2 x y z = 0 0 0

x = 0 5 2 y + 5 - 1 - 2 2 z = 0 ⇒ x = 0 y = 1 + 2 z

z 2 + 3 + 2 2 z 2 = 1 ⇒ z = 1 4 + 2 2

Logo o autovetor de norma 1 correspondente é e 2 = 0 , 2 + 1   4 + 2 2 , 1 4 + 2 2

λ = - 5 2 - 1 2

5 2 + 7 2 0 0 0 5 1 + 2 2 5 2 0 5 2 5 - 1 + 2 2 x y z = 0 0 0

x = 0 5 2 y + 5 - 1 + 2 2 z = 0 ⇒ x = 0 y = 1 - 2 z

z 2 + 3 - 2 2 z 2 = 1 ⇒ z = 1 4 - 2 2

Logo o autovetor de norma 1 correspondente é e 3 = 0 , 1 - 2 4 - 2 2 , 1 4 - 2 2

A base de autovetores é então: B = 1,0 , 0 , 0 , 2 + 1   4 + 2 2 , 1 4 + 2 2 , 0 , 1 - 2 4 - 2 2 , 1 4 - 2 2

Assim as substituições lineares são nada mais que os vetores de B   escritos em função dos vetores de C a n :

x 2 = x 1

y 2 = 2 + 1 4 + 2 2 y 1 + 1 4 + 2 2 z 1  

z 2 = 1 - 2 4 - 2 2 y 1 + 1 4 - 2 2 z 1

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

Elaboração própria

Ache a equação canônica de:

x y = 1

E indique a substituição linear utilizada.

Passo 1

Aqui queremos achar a equação da quádrica numa base em que não apareçam os termos mistos,e além disso dizer como as variáveis x 2 , y 2 se relacionam com x 1 , y 1   . Pra isso precisamos achar a base para a qual passamos quando fazemos a diagonalização da matriz.

Passo 2

Temos que:

q C a n = 0 1 2 1 2 0

Calculando os autovalores:

det ⁡ q C a n - λ I = - λ 1 2 1 2 - λ = 0

λ 2 - 1 4 = 0

λ 1 = 1 2 λ 2 = - 1 2

Logo uma equação reduzida é:

1 2 x 2 - 1 2 y 2 = 1

Passo 3

Agora os autovetores:

λ = 1 2

1 2 1 2 1 2 1 2 x y = 0 0

1 2 x + 1 2 y = 0 ⇒ x = - y

x 2 + x 2 = 1 ⇒ x = 2 2

Logo o autovetor de norma 1   associado é e 1 = 2 2 , - 2 2

λ = - 1 2

- 1 2 1 2 1 2 - 1 2 x y = 0 0

- 1 2 x + 1 2 y = 0 ⇒ x = y

x 2 + x 2 = 1 ⇒ x = 2 2

Logo o autovetor de norma 1   associado é e 2 = 2 2 , 2 2

A base de autovetores é então B = 2 2 , - 2 2 , 2 2 , 2 2

As substituições lineares que foram pedidos não são nada mais do que expressar os vtores de B   em termos dos vetores de C a n

x 2 = 2 2 x 1 - 2 2 y 1

y 2 = 2 2 x 1 + 2 2 y 1

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #9

Callioli, C.A; Domingues, H.H. e Costa, R.C.F., Álgebra Linear e Aplicações, 4a. edição, São Paulo, Atual, 1983.

Ache a equação canônica de:

x 2 + y ² - 2 x y + x = 1

Passo 1

Agora nós estamos lidando com um termo linear, portanto devemos fazer todo o esquema da teoria. O jeito de resolver você já tem direitinho, agora troca os valores e se faz de computadorzinho.

Passo 2

Temos que:

q C a n = 1 - 1 - 1 1

Calculando os autovalores:

det ⁡ q C a n - λ I = 1 - λ - 1 - 1 1 - λ = 0

λ 2 - 2 λ + 1 - 1 = 0

λ 1 = 0 , λ 2 = 2

Passo 3

Agora os autovetores:

λ = 0

1 - 1 - 1 1 x y = 0 0

x - y = 0 ⇒ x = y

x 2 + x 2 = 1 ⇒ x = 2 2

Logo o autovetor de norma 1   associado é e 1 = 2 2 , 2 2

λ = 2

- 1 - 1 - 1 - 1 x y = 0 0

- x - y = 0 ⇒ x = - y

x 2 + x 2 = 1 ⇒ x = 2 2

Logo o autovetor de norma 1   associado é e 2 = 2 2 , - 2 2

A base de autovetores é então B = 2 2 , 2 2 , 2 2 , - 2 2

Passo 4

Achamos a matriz de mudança de base:

I d C a n ← B = 2 2 2 2 2 2 - 2 2

E temos que

x 1 = 1 0 x 1 y 1

x 1 y 1 = 2 2 2 2 2 2 - 2 2 x 2 y 2

x 1 = 1 0 2 2 2 2 2 2 - 2 2 x 2 y 2 = 2 2 2 2 x 2 y 2 = 2 2 x 2 + 2 2 y 2

Logo a equação após a rotação é:

2 y 2 + 2 2 x + 2 2 y = 1

Passo 5

Completando os quadrados:

2 y 2 + 2 2 y + 1 16 + 2 2 x = 17 16

2 y + 1 4 2 + 2 2 x = 17 16

2 y + 2 8 2 + 2 2 x = 17 16

Fazendo x 3 = x 2 e y 3 = y 2 + 2 8 , chegamos finalmente em:

2 y 2 + 2 2 x = 17 16

Resposta

2 y 2 + 2 2 x = 17 16

Exercício Resolvido #10

Elaboração própria

Ache a equação canônica de:

y 2 + 2 x y + 4 x z + 2 y z + 6 x + 2 y - 2 z - 3 = 0

Passo 1

Agora nós estamos lidando com termos lineares, portanto devemos fazer todo o esquema da teoria. O jeito de resolver você já tem direitinho, agora troca os valores e se faz de computadorzinho.

Passo 2

Temos que:

q C a n = 0 1 2 1 1 1 2 1 0

Calculando os autovalores:

det ⁡ q C a n - λ I = - λ 1 2 1 1 - λ 1 2 1 - λ = 0

λ 2 1 - λ + 2 + 2 - 4 1 - λ + λ + λ = 0

- λ 3 + λ 2 + 6 λ = λ - λ 2 + λ + 6 = 0

λ 1 = 0 ,   λ 2 = - 2 ,   λ 3 = 3

Passo 3

λ = 0

0 1 2 1 1 1 2 1 0 x y z = 0 0 0

2 x + y = 0 y + 2 z = 0 ⇒ z = x y = - 2 x

x 2 + x 2 + 4 x 2 = 1 ⇒ x = 6 6

Logo o autovetor de norma 1 correspondente é e 1 = 6 6 , - 2 6 6 , 6 6

λ = - 2

2 1 2 1 3 1 2 1 2 x y z = 0 0 0

2 x + y + 2 z = 0 x + 3 y + z = 0 ⇒ y = 0 z = - x

x 2 + x 2 = 1 ⇒ x = 2 2

Logo o autovetor de norma 1 correspondente é e 2 = 2 2 , 0 , - 2 2

λ = 3

- 3 1 2 1 - 2 1 2 1 - 3 x y z = 0 0 0

- 3 x + y + 2 z = 0 2 x + y - 3 z = 0 ⇒ z = x y = x

x 2 + x 2 + x 2 = 1 ⇒ x = 3 3

Logo o autovetor de norma 1 correspondente é e 3 = 3 3 , 3 3 , 3 3

Assim, a base de autovetores é B = 6 6 , - 2 6 6 , 6 6 , 2 2 , 0 , - 2 2 , 3 3 , 3 3 , 3 3 .

Passo 4

Achamos a matriz de mudança de base:

I d C a n ← B = 6 6 2 2 3 3 - 2 6 6 0 3 3 6 6 - 2 2 3 3

E temos que

6 x 1 + 2 y 1 - 2 z 1 = 6 2 - 2 x 1 y 1 z 1

x 1 y 1 z 1 = 6 6 2 2 3 3 - 2 6 6 0 3 3 6 6 - 2 2 3 3 x 2 y 2 z 2

6 x 1 + 2 y 1 - 2 z 1 = 6 2 - 2 6 6 2 2 3 3 - 2 6 6 0 3 3 6 6 - 2 2 3 3 x 2 y 2 z 2

6 x 1 + 2 y 1 - 2 z 1 = 0 4 2 2 3 x 2 y 2 z 2 = 4 2 y 2 + 2 3 z 2

Logo a equação após a rotação é:

- 2 y 2 + 3 z 2 + 4 2 y + 2 3 z - 3 = 0

Passo 5

Completando os quadrados:

- 2 y 2 - 4 2 y + 4 + 3 z 2 + 2 3 z + 1 - 3 = - 4 + 1

- 2 y - 2 2 + 3 z + 1 2 = 0

- 2 y - 2 2 + 3 z + 3 3 2 = 0

Fazendo então:

y 3 = y 2 - 2

z 3 = z 2 + 3 3

Chegamos por fim na equação:

- 2 y 2 + 3 z 2 = 0

Resposta

- 2 y 2 + 3 z 2 = 0

Exercícios de Livros Relacionados

Por uma conveniente translação de eixos, transformar cada uma das equações seguintes na forma reduzida e identificar a quádrica que ela representa. x 2 + y 2 - 2 y = 0
Efetuar uma rotação e uma translação de eixos para referir a quádrica ao sistema O ' X Y Z e identifica-la. 2 x 2 + 2 y 2 + 5 z 2 - 4 x y - 2 x z + 2 y z - 10 x - 6 y - 2 z - 7 = 0
Efetuar uma rotação e uma translação de eixos para referir a quádrica ao sistema O ' X Y Z e identifica-la. 3 x 2 + 5 y 2 + 3 z 2 - 2 x y + 2 x z - 2 y z - 4 x + 6 y - 2 z + 2 = 0
Por uma conveniente translação de eixos, transformar a equação na forma reduzida e identificar a quádrica que ela representa. 2 x 2 - y 2 - 2 z 2 + 8 x + 4 = 0
Por uma conveniente translação de eixos, transformar a equação na forma reduzida e identificar a quádrica que ela representa. 3 x 2 + 4 y 2 + 24 x - 8 y + 24 z + 100 = 0