Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Base - Álgebra Linear

Ver Todos os Exercícios

Teoria

E aí? Bem vindo ao Responde Aí! Vamos nessa aprender tudo sobre a Base de um espaço vetorial!

O que é a Base de um Espaço Vetorial?

A base de um espaço vetorial é um conjunto de vetores linearmente independentes que definem um espaço vetorial.

-Hãam? 😖

Vamos ver um exemplo pra ficar mais claro!

O plano cartesiano é nada mais nada menos do que um espaço vetorial em duas dimensões! Para esse plano existir, a gente precisa de um vetor que aponte pra cima (o eixo y) e um vetor que aponte pro lado (o eixo x).

Ou seja, para definir o espaço eu poderia utilizar os vetores linearmente independentes e :

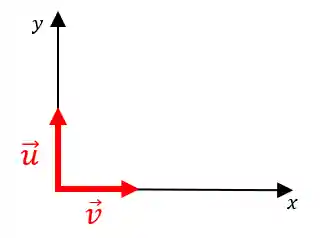
Plano cartesiano e os vetores
Plano cartesiano e os vetores

Viu, o conceito é tranquilo de entender! Agora vamos escrever uma base do conjunto , para isso a gente vai precisar de três vetores:

Cada um dos vetores de aponta para uma das três direções :

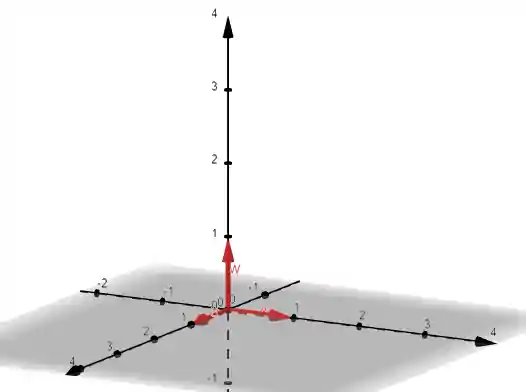
Base do
Base do

É muito importante que a base seja Linearmente Independente, por exemplo, observe os seguintes três vetores.

Nos vetores de a gente tem uma dependência linear, afinal se somarmos o primeiro e o segundo vetor, temos o terceiro vetor como resultado. Agora vamos desenhar esses vetores:

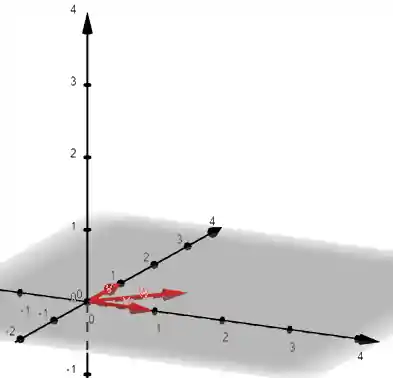
Vetores linearmente dependentes
Vetores linearmente dependentes

Opa, nenhum dos três vetores aponta pra cima! Ou seja, com esses três vetores a gente pode apontar para qualquer direção de ou de , mas é impossível apontar para cima ou para baixo. Então eles não formam uma base no .

Entendeu a importância dos vetores serem ?

Se liga nesse vídeo supercompleto que o Responde Aí preparou pra você sobre bases de um espaço vetorial! 👇

Continuando…um detalhe bastante importante é que um mesmo espaço vetorial pode ter várias bases! Afinal de contas, para formar uma base, a gente só precisa de um conjunto de vetores linearmente independentes, então todos os conjuntos abaixo são bases válidas do .

Pra que serve a base de um espaço vetorial?

A ideia por trás de uma base é que: aplicando operações nos vetores da base, nós podemos gerar qualquer outro vetor do espaço vetorial. Por exemplo, pense num vetor de duas dimensões aleatório! Eu vou escolher o vetor . A gente pode escrever esse vetor aplicando somas e multiplicações em uma base de . Pra exemplificar, vou usar a base :

Bases canônicas

No exemplo acima pode ficar um pouco difícil de enxergar como encontramos os valores que multiplicam os vetores da base. Pra facilitar esse trabalho, a gente costuma utilizar as bases de espaço vetorial canônicas: Essas são bases compostas apenas por ’s e ’s. Por exemplo:

Assim, quando a gente quiser escrever um vetor qualquer, fica fácil de saber como ele é gerado pela base canônica. Por exemplo, o vetor é simplesmente:

Base de um espaço matricial

O mais interessante de álgebra é que a gente consegue extrapolar esse conceito de bases, para além de vetores, e falar sobre por exemplo, a base canônica de matrizes . A base para :

Outra base para matrizes é:

Agora vamos praticar com exercícios?

Pra que serve a base de um espaço vetorial?

Bases canônicas

Base de um espaço matricial

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ-P1-2013.2

Seja H o subespaço definido por:

H =   < 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4 ,   0 ,   2 ,   - 4 >

Qual dos conjuntos abaixo é base de H ?

a   { 2 , - 1 ,   - 1 }

b   { 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4 ,   0 ,   2 ,   - 4 }

c   { 2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 }

d   2 , - 1 ,   - 1 ,   2 ,   - 2 ,   1 ,   - 4 ,   1 ,   4

Passo 1

O subespaço H é formado por vetores do R 3 .

Como H é um subconjunto do R 3 então tem dimensão 3, então sua base deve ter no máximo 3 vetores.

Já descartamos a letra ( b ) !

Passo 2

Repare que os dois primeiros vetores de H , ( 2 , - 1 , - 1 ) e ( 2 , - 2,1 ) são L I , já que não são múltiplos um do outro (lembra que para vetores LI, Linearmente Independentes, não podem ser escritos como combinação linear um do outro). Então concluímos que a letra (c) é um conjunto L I (guarda essa informação!).

Então veja bem, os dois vetores ( 2 , - 1 , - 1 ) e ( 2 , - 2,1 ) formam um subespaço de H de dimensão 2 , então o nosso espaço vetorial H tem que ter dimensão no mínimo 2 , certo?

Assim eu descarto a letra ( a ) , que tem apenas um vetor na base (dimensão 1 ).

Passo 3

Agora é o seguinte, sabemos que para um conjunto de vetores ser uma base esse conjunto precisa ser L I , então concluímos que:

  • Se o conjunto da letra ( d ) for L I , ele já é uma base, e a resposta é ( d )
  • Se o conjunto da letra ( d ) for L D , ele não é uma base, então a resposta é ( c ) , pois já sabemos que ( c ) é L I

Para descobrirmos se os vetores de ( d ) são L I , basta jogarmos eles numa matriz e escalonarmos:

2 - 1 - 1 2 - 2 1 - 4 1 4 → L 2 ← L 2 - L 1 L 3 ← L 3 + 2 L 1 2 - 1 - 1 0 - 1 2 0 - 1 2 → L 3 ← L 3 - L 2 2 - 1 - 1 0 - 1 2 0 0 0

Opa! Acabamos de descobrir que os vetores de ( d ) são L D (Linearmente Dependentes)! Então, a resposta só pode ser a letra ( c ) !

Resposta

Letra ( c )

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 96 – Ex. 61

Mostrar que o conjunto

2 3 - 1 0 ,   1 - 1 0 - 2 ,   - 3 - 2 1 - 1 ,   3 - 7 - 2 5

É uma base de M 2 × 2 .

Passo 1

Como as matrizes já são do tipo 2 × 2 , basta só verificar que o conjunto é L I , pois, consequentemente, espaço gerado desse conjunto dará todas as matrizes 2 × 2 .

a 2 3 - 1 0 + b 1 - 1 0 - 2 + c - 3 - 2 1 - 1 + d 3 - 7 - 2 5 = 0 ⇒

2 a + b - 3 c + 3 d = 0 3 a - b - 2 c - 7 d = 0 - a + c - 2 d = 0 - 2 b - c + 5 d = 0

Bom esse sistema ficou meio grande, né? Acho que a melhor forma de resolvê-lo é por escalonamento. Para isso vamos passar para a forma matricial:

2 1 - 3 3 3 - 1 - 2 - 7 - 1 0 1 - 2 0 - 2 - 1 5 ⋅ a b c d = 0

Passo 2

Se você fizer o escalonamento da matriz dos coeficientes desse sistema, veremos que dá:

2 1 - 3 3 0 - 5 2 5 2 - 23 2 0 0 - 3 71 5 0 0 0 - 14 5 ⋅ a b c d = 0 ⇒

2 a + b - 3 c + 3 d = 0 ⇒ 2 a = 0 ⇒ a = 0 - 5 2 b + 5 2 c - 23 2 d = 0 ⇒ - 5 2 b = 0 ⇒ b = 0 - 3 c + 71 5 d = 0 ⇒ - 3 c = 0 ⇒ c = 0 - 14 5 d = 0 ⇒ d = 0

E como podemos ver, de fato o conjunto forma uma base para M 2 × 2 .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 99 – Ex. 74 – b)

Seja o subespaço S de M 2 × 2 :

S = a b c d c = a + b   e   d = a }

O conjunto

1 - 1 0 1 ,   2 1 3 4

É uma base de S ?

Passo 1

Para compararmos, precisamos saber antes quem é a base de S . Sendo assim, vamos encontrar os geradores para o conjunto:

a b c d = a b a + b a = a 1 0 1 1 + b 0 1 1 0

Ihhh caramba, os vetores deram diferentes então não é uma base correto?? ERRADO!! Se essas matrizes que achamos forem uma C L , da base indicada no enunciado, não tem problema algum! Sendo assim, vamos verificar isso.

Passo 2

Se você perceber podemos escrever 1 - 1 0 1 como uma C L de 1 0 1 1 , 0 1 1 0 :

1 - 1 0 1 = 1 0 1 1 - 0 1 1 0

Então a matriz 1 - 1 0 1 é valida!

Já a segunda vamos calcular no braço:

2 1 3 4 = a 1 0 1 1 + b 0 1 1 0 ⇒

2 = a 1 = b 3 = a + b 4 = a

Como podemos ver a primeira e a última equação se contradizem e, portanto, a equação é impossível. Logo, 2 1 3 4 não é uma C L de 1 0 1 1 , 0 1 1 0 e o conjunto do enunciado não é uma base de S .

Resposta

Não é uma base de S

Exercício Resolvido #4

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 96 – Ex. 60 (Adaptado)

Quais dos seguintes conjuntos de polinômios formam base de P 2 ?

  1. 2 t 2 + t - 4 ,   t 2 - 3 t + 1
  2. 1 ,   t ,   t 2
  3. 2 ,   1 - x ,   1 + x 2
  4. 1 + x + x 2 ,   x + x 2 ,   x 2
  5. { 1 + x ,   x - x 2 ,   1 + 2 x - x 2 }  

Passo 1

De cara, podemos ver que a letra a) não pode ser uma base pois só possui dois polinômios. Sendo assim a dimensão máxima do conjunto é 2 e como a dimensão de P 2 é 3 , não pode ser uma base.

Por sua vez a letra b) é a base canônica de P 2 e, portanto, é uma base de P 2 .

Passo 2

Agora, para o resto das letras só nos resta verificar se os polinômios são L I ...

Letra c)

a 2 + b 1 - x + c 1 + x 2 = 0 ⇒

2 a + b - b x + c + c x 2 = 0 ⇒

2 a + b + c - b x + c x 2 = 0 ⇒

2 a + b + c = 0 ⇒ 2 a = 0 ⇒ a = 0 - b = 0 ⇒ b = 0 c = 0

Como achamos que os coeficientes são a = b = c = 0 , então o conjunto é L I .

Letra d)

a 1 + x + x 2 + b x + x 2 + c x 2 = 0 ⇒

a + a x + a x 2 + b x + b x 2 + c x 2 = 0 ⇒

a + a + b x + a + b + c x 2 = 0 ⇒

a = 0 a + b = 0 ⇒ b = 0 a + b + c = 0 ⇒ c = 0

Como achamos que os coeficientes são a = b = c = 0 , então o conjunto é L I .

Passo 3

Letra e)

a 1 + x + b x - x 2 + c 1 + 2 x - x 2 = 0 ⇒

a + a x + b x - b x 2 + c + c 2 x - c x 2 = 0 ⇒

a + c + a + b + 2 c x + - b - c x 2 = 0 ⇒

a + c = 0 ⇒ a = - c a + b + 2 c = 0 ⇒ - c - c + 2 c = 0 ⇒ 0 = 0   ( O K ! ) - b - c = 0 ⇒ b = - c

Como podemos ver, temos que a = b = - c e quando tentamos descobrir o valor de c substituindo na segunda equação, chegamos em 0 = 0 e ela não nos diz nada. Sendo assim, c é uma variável livre e pode assumir qualquer valor. Logo, o conjunto é L D e, portanto, não é uma base de P 2 .

Resposta

Letra b), c), d).

Exercício Resolvido #5

UFRJ-P1-2013.2

Seja V um espaço vetorial e S = { v 1 → ,   v 2 → ,   v 3 → ,   v 4 → } um conjunto de vetores de V , todos distintos entre si.

Sejam A = { v 1 → ,   v 2 → } e B = { v 3 → ,   v 4 → } .

Assinale a alternativa VERDADEIRA:

( a ) Se S é um conjunto linearmente independente ( L I ), então A é um conjunto linearmente independente ( L I ) e B é um conjunto linearmente independente ( L I ).

( b ) Se S é um conjunto gerador de V , então A é um conjunto gerador de V e B é um conjunto gerador de V

( c ) Se S é um conjunto linearmente independente (LI), ou A é um conjunto linearmente independente (LI), ou B é um conjunto linearmente independente (LI), mas não ambos.

( d ) Se S é um conjunto gerador de V , então: ou A é um conjunto gerador de V , ou B é um conjunto gerador de V , mas não ambos.

Passo 1

É, parece que teremos que olhar uma a uma! : (

Vamos lá.

Na letra ( a ) , o conjunto S é L I .

Isso significa que nenhum vetor é combinação linear do outro.

Portanto:

  • v 1 → não é combinação linear de v 2 → , nem vice-versa. Então o conjuto A tem que ser L I , pois A só tem esses dois vetores!
  • v 3 → não é combinação linear de v 4 → nem vice-versa. Então o conjunto B tem que ser L I , pois B só tem esses dois vetores!

Então a letra ( a ) é verdadeira!

(Mas vamos ainda descobrir se realmente as outras são falsas...)

Passo 2

Na letra ( b ) , o conjunto S é conjunto gerador de V .

Isso não diz se S é L I ou L D , apenas que ele gera V .

Se S for L I , por exemplo, S é uma base de V . Isso significa que, qualquer vetor que eu tire da base, aquele conjunto lá não vai mais gerar V .

Então, se tirarmos os vetores v 3 → e v 4 → , teremos o conjunto A , e ele não vai mais gerar V , e sim um outro espaço menor.

Então essa não pode ser verdadeira, pois nem sempre o A vai ser gerador de V (nem o B , analogamente).

Passo 3

Na letra ( c ) , o conjunto S é L I .

Como já vimos lá no passo 1, tanto A como B tem que ser L I , obrigatoriamente.

Então o “mas não ambos” no final da afirmação diz que os dois não podem ser L I .

Esse aí tem que ser falsa, então.

Passo 4

Na letra ( d ) , o conjunto S é gerador de V .

No passo 2 já vimos que pode acontecer de nem o A nem o B serem conjuntos geradores de V (que é o caso em que S é L I ).

Falsa.

Resposta

Letra a

Exercício Resolvido #6

UFRJ-P2-2013.1

Sejam u 1 → ,   … ,   u n → vetores gerando um espaço vetorial V .

Sejam v 1 → ,   … ,   v k → ∈ V , vetores linearmente independentes.

Assinale a alternativa VERDADEIRA:

a   n ≥ k

b   n = k

c   n ≤ k

d   n > k

Passo 1

Se v 1 → , … ,   v k → são L I , então { v 1 → , … ,   v k → } é uma base de algum subespaço vetorial de V .

Né não?

Então a dimensão de ⟨ v 1 → , … ,   v k → ⟩ é k .

Só que ⟨ v 1 → , … ,   v k → ⟩ pertence a V , então sua dimensão tem que ser menor ou igual à dimensão de V .

k ≤ dim ⁡ V

Passo 2

Agora vamos pensar no outro conjunto, { u 1 → ,   … u n → } .

Esse conjunto tem n vetores, certo?

Se o conjunto for L I , então n = dim ⁡ V , já que nesse caso ele é base de V .

Mas como a questão não explicitou, logo o conjunto é L D , então n tem que ter mais vetores que a base, n ≥ dim ⁡ V .

A conclusão que você chega é:

n ≥ dim ⁡ V

Passo 3

Agora é só ligar as duas informações:

k ≤ dim ⁡ V ≤ n

Logo:

k ≤ n

A única letra que diz isso é letra ( a ) ( n ≥ k ).

Resposta

Letra ( a )

Exercícios de Livros Relacionados

Demonstrar que é L.I o conjunto { 1 ,x - a ,x - a 2 ,… ,x - a n - 1 } De vetores de P n - 1 ( R ) , onde a é um número arbitrário.
Quais dos conjuntos de vetores dados são bases de P 2 ?c) 1 +x +x 2 ,x +x 2 ,x 2
Quais dos conjuntos de vetores dados são bases de P 2 ?a) 1 -3 x +2 x 2 ,1 +x +4 x 2 ,1 -7 x
Verificar quais dos seguintes conjuntos de vetores formam base do R 2 . { 1 ,2 ,- 1 ,3 } { 3 ,- 6 ,- 4 ,8 } { 0 ,0 ,2 ,3 } { 3 ,- 1 ,2 ,3 }
Prove que vec u = 0 = vec u = (0 , 0 , 0)_E .