Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Subespaço Vetorial

Ver Todos os Exercícios

Teoria

Opa! Bora conversar sobre subespaço vetorial?

O que é um Subespaço Vetorial?

O Subespaço Vetorial é simplesmente um subconjunto do espaço vetorial! Sua definição formal é escrita da seguinte forma:

Seja um espaço vetorial . Dizemos que o subconjunto é um subespaço vetorial se é ele mesmo um espaço vetorial.

Mas tem mais! Para um conjunto ser um subespaço vetorial ele deve obedecer a alguns requisitos. Saca só:

Seja um espaço vetorial. O subconjunto é um subespaço vetorial se:

  • é fechado para soma:
  • é fechado para multiplicação por escalar:

Mas se você ta perdidinho, não tá entendendo nada…Vem cá, me dá a mão e a gente vai entender como esse negócio de subespaço vetorial funciona na prática! Imagina que o espaço vetorial é uma caixa bem grande, os Subespaços são caixinhas ainda menores ali dentro formando subespaços:

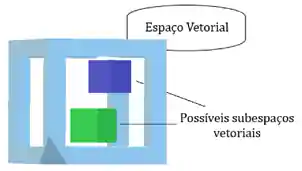
Espaço e subespaço vetorial
Espaço e subespaço vetorial

O subespaço também é um espaço vetorial!! Se comporta da mesma forma que o espaço vetorial e possui as mesmas operações do espaço que o contém, a única diferença é que ele está contido em um espaço vetorial maior.

📢 Clique para ver mais:

Requisitos de Subespaço Vetorial

Os requisitos que um conjunto deve ter para ser considerado um subespaço vetorial são aqueles apresentados lá no início, daquele jeito formal. Mas agora a gente vai explicar melhor!

1) O é o elemento neutro da soma em espaços vetoriais

Então para um mini conjunto dentro do espaço vetorial ser considerado subespaço vetorial ele precisa conter o elemento 00, porque um subespaço vetorial também é um espaço vetorial. Vamos supor que uma bolinha vermelha é o elemento neutro.

Na figura abaixo a bolinha vermelha está dentro apenas do conjunto verde, então o conjunto azul já perdeu a chance de ser subespaço vetorial.

Elemento neutro de um subespaço vetorial
Elemento neutro de um subespaço vetorial

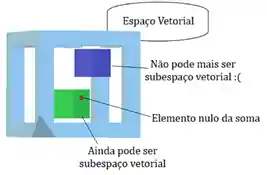
2) A soma de vetores dentro do subespaço vetorial tem que resultar em outro vetor que também esteja contido dentro desse subespaço vetorial

Esse requisito faz muito sentido, afinal um subespaço vetorial também é um espaço vetorial. Lembrando que para que um conjunto seja considerado um espaço vetorial a soma de vetores dentro desse espaço tem que resultar em outro vetor que também esteja contido dentro do espaço vetorial!

3) A multiplicação de um vetor do subespaço por um escalar também tem que resultar em um vetor pertencente ao subespaço.

Esse requisito segue a mesma lógica que o anterior!

Como saber se um Conjunto é Subespaço Vetorial

Então, se você tem um conjunto qualquer e quer saber se ele é um subespaço vetorial você precisa testar cada um desses três requisitos e se ele atender a todos ele é um subespaço vetorial se não atender a pelo menos um então não é subespaço vetorial.

Considere o seguinte conjunto:

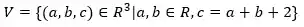
conjunto V
conjunto V

E considere também que as operações dentro do conjunto são as operações usuais. Ele é ou não é um subespaço vetorial?

Primeiro vamos testar se esse conjunto contém o elemento neutro. No e com operações usuais o elemento neutro é o , então temos que ver se ele pertence ao subespaço. Vamos substituir , e por na expressão para e vê se encontramos uma relação verdadeira:

Eita, isso não é verdadeiro, isso quer dizer que o elemento nulo não pertence a e portanto, não é um subespaço vetorial!

Agora vamos praticar com exercícios?!

Requisitos de Subespaço Vetorial

Como saber se um Conjunto é Subespaço Vetorial

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 2ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 86 - problema 3.1.

Determine se é subespaço vetorial de R 3 :

a   U = a , b , c ∈ R 3 a , c ∈ R ,   b = a + c + 1 }

b   V = a , b , c ∈ R 3 a , b ∈ R ,   2 a + 3 b = 5 c }

c   K = a , 1,1 ∈ R 3 a ∈ R }

Passo 1

( a ) Para testar se U é um subespaço vetorial de   R 3 , precisamos aplicar o teorema.

Sabemos que o elemento nulo de R 3 é o vetor ( 0 , 0,0 ) .

Aplicando na condição do conjunto da letra ( a ) este vetor, temos

0 = 0 + 0 + 1

0 = 1

Como sabemos que 0 não é igual a 1 , chegamos a um absurdo. Logo, o elemento nulo não está contido nesse conjunto e, portanto, não é um subespaço vetorial de R 3 .

Passo 2

( b ) Vamos aplicar o teorema! De cara podemos ver que

2 ∙ 0 + 3 ∙ 0 = 5 ∙ 0

0 = 0

Portanto, o 0 pertence ao conjunto.

Passo 3

Mas, calma, isso ainda não prova nada... Vamos para a segunda condição do teorema.

Sendo

v 1 = a 1 , b 1 , c 1 ,   v 2 = a 2 , b 2 , c 2

v 1 , v 2 ∈ V ⇒ v 1 + v 2 ∈ V ?

Como

v 1 + v 2 = ( a 1 + a 2 , b 1 + b 2 , c 1 + c 2 )

Aplicando as condições do conjunto temos que:

2 a 1 + a 2 + 3 b 1 + b 2 = 5 c 1 + c 2

2 a 1 + 3 b 1 + 2 a 2 + 3 b 2 = 5 c 1 + c 2

Repare que na nossa implicação no começo do enunciado, usamos a hipótese de: v 1 , v 2 ∈ V . Isso siginifca que eles pertencem ao conjunto e, portanto, cada uma das suas coordenadas satisfaz a equação descrita. Assim, aplicando a hipótese, temos que que:

2 a 1 + 3 b 1 = 5 c 1   e   2 a 2 + 3 b 2 = 5 c 2

Continuando:

2 a 1 + 3 b 1 + 2 a 2 + 3 b 2 = 5 c 1 + c 2

5 c 1 + c 2 = 5 c 1 + c 2

E assim está fechado para soma.

Passo 4

Última condição do teorema:

λ ∈ R ,   v = a , b , c ∈ V ⇒ λ v ∈ V ?

Temos

λ v = ( λ a , λ b , λ c )

Logo, aplicando a condição do conjunto ficaríamos com:

2 λ a + 3 λ b = 5 λ c

λ 2 a + 3 b = λ ( 5 c )

Com isso, ao aplicarmos a hipótese v = a , b , c ∈ V , vemos que:

2 a + 3 b = 5 c

Assim, podemos concluir que:

λ 2 a + 3 b = λ ( 5 c )

λ 5 c = λ 5 c

E é fechado para multiplicação por escalar. Logo, é um subespaço vetorial de R 3 .

Passo 5

Na letra ( c ) podemos ver também de cara que não é um subespaço vetorial!

Basta ver que como o conjunto é composto de elementos do tipo ( a , 1,1 ) , é impossível algum elemento desse conjunto ser o vetor ( 0,0 , 0 ) .

Como ele não possui o elemento nulo do R 3 , ele não é subespaço vetorial.

Resposta

  1. Não é subespaço vetorial.
  2. É subespaço vetorial.
  3. Não é subespaço vetorial.

Exercício Resolvido #2

PUC-RIO, Lista 3 de monitoria para a P1, 2015.1, Exercício 2.

Considere o subconjunto de M 2 × 2 definido por:

Z = A ∈ M 2 × 2 A ∙ 1 - 2 = 0 0 }

Z é um subespaço vetorial de M 2 × 2 ?

Passo 1

Perceba que o conjunto em questão possui como elemento matrizes 2 × 2 . Logo, são esses elementos que temos que testar, para ver se é ou não subespaço vetorial.

Passo 2

0 ∈ Z ?

Podemos ver que a matriz nula, A = 0 0 0 0 satisfaz as condições do conjunto. Pois

A ∙ 1 - 2 = 0 0

Logo, a resposta é sim.

Passo 3

A 1 , A 2 ∈ Z ⇒ A 1 + A 2 ∈ Z ?

Tudo bem então vamos verificar se a soma satisfaz as condições do problema.

A 1 + A 2 ∙ 1 - 2 = 0 0 ⇒ A 1 ∙ 1 - 2 + A 2 ∙ 1 - 2 = 0 0   1

Agora, aplicamos a hipótese: A 1 , A 2 ∈ Z , que significa que ambas as matrizes satisfazem a condição do conjunto:

A 1 ∙ 1 - 2 = 0 0

A 2 ∙ 1 - 2 = 0 0

Substituindo em 1 :

A 1 ∙ 1 - 2 + A 2 ∙ 1 - 2 = 0 0

0 0 + 0 0 = 0 0

Os dois lados da equação são iguais. Logo, está fechado para soma.

Passo 4

λ ∈ R ,   A ∈ M 2 × 2 ⇒ λ A ∈ M 2 × 2 ?

Temos que:

λ A ∙ 1 - 2 = 0 0

λ A ∙ 1 - 2 = 0 0

Ao aplicarmos nossa hipótese, temos que:

A ∙ 1 - 2 = 0 0

λ ∙ 0 0 = 0 0

E, assim, vemos que para qualquer λ real:

0 0 = 0 0

Logo está fechado para a multiplicação por escalar, concluindo que Z é um subespaço vetorial de M 2 × 2 .

Resposta

Sim, Z é um subespaço vetorial de M 2 × 2

Exercício Resolvido #3

PUC-RIO, Lista de monitoria 5 para P1, 2015.1, Exercício 1, Letra a

Mostre que o conjunto abaixo é subespaço vetorial de P 2 , com as operações usuais de P 2 :

S = a + b x + c x 2 ∈ P 2 a + 3 b - 2 c = 0 }

Passo 1

Vamos testar o teorema!

  • 0 ∈ S ?
  • p 1 ( x ) , p 2 ( x ) ∈ S ⇒ ( p 1 + p 2 ) ( x ) ∈ S   ?
  • λ ∈ R ,   p ( x ) ∈ S ⇒ ( λ p ) ( x ) ∈ S ?

Passo 2

Será que o polinômio nulo, 0 + 0 x + 0 x 2 , satisfaz as condições de S ?

0 + 3 ∙ 0 - 2 ∙ 0 = 0

0 = 0

Portanto, sim, satisfaz.

Passo 3

Sendo p 1 + p 2 x = a 1 + a 2 + b 1 + b 2 x + c 1 + c 2 x 2 , será que satisfaz as condições de S ? Vamos ver:

a 1 + a 2 + 3 b 1 + b 2 - 2 c 1 + c 2 = 0

a 1 + a 2 + 3 b 1 + 3 b 2 - 2 c 1 - 2 c 2 = 0

Reagrupando:

a 1 + 3 b 1 - 2 c 1 + a 2 + 3 b 2 - 2 c 2 = 0

Repare que a 1 ,   b 1 ,   c 1 são exatamente os coeficientes de p 1 ( x ) . Assim como a 2 , b 2 , c 2 são os de p 2 ( x ) .

POR HIPÓTESE, ambos pertencem ao conjunto. Sendo assim, seus coeficientes satisfazem à relação do conjunto, que é a 1 + 3 b 1 - 2 c 1 = 0 e a 2 + 3 b 2 - 2 c 2 = 0 . Logo, voltando para a última equação e aplicando as hipóteses temos:

a 1 + 3 b 1 - 2 c 1 + a 2 + 3 b 2 - 2 c 2 = 0

0 + 0 = 0

Passo 4

Agora só falta a multiplicação por escalar! Sabendo que λ p x = λ a + λ b x + λ c x 2 , vamos aplicar a condição do conjunto:

λ a + 3 λ b - 2 λ c = 0 ⇒

λ a + 3 b - 2 c = 0

Já que a ,   b ,   c   são exatamente os coeficientes de p ( x ) , e p x ∈ S , seus coeficientes satisfazem o conjunto e, portanto, a + 3 b - 2 c = 0 . Logo:

λ ∙ 0 = 0

0 = 0

Concluímos que, de fato, S é subespaço vetorial de P 2 .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

PUC-RIO, Lista de Monitoria 4, 2015.1, Exercício 1, Letra g, Adaptado

Mostre que o conjunto:

S = p ∈ P 3 p - 1 = p 1 = 0 }

é um subespaço vetorial de P 3 , com as mesmas operações usuais dele.

Passo 1

Queremos verificar:

  • 0 ∈ S ?
  • p 1 ( x ) , p 2 ( x ) ∈ S ⇒ ( p 1 + p 2 ) ( x ) ∈ S   ?
  • λ ∈ R ,   p ( x ) ∈ S ⇒ ( λ p ) ( x ) ∈ S ?

Passo 2

  • 0 ∈ S ?

Sim, como o conjunto possui a condição p - 1 = p 1 = 0 = 0 + 0 x + 0 x 2 + 0 x 3 , o conjunto contém o polinômio nulo.

Passo 3

  • p 1 ( x ) , p 2 ( x ) ∈ S ⇒ ( p 1 + p 2 ) ( x ) ∈ S   ?

Para ver se está fechado para soma, basta fazer:

p 1 + p 2 - 1 = p 1 - 1 + p 2 - 1 = 0 + 0

E também que:

p 1 + p 2 1 = p 1 1 + p 2 1 = 0 + 0

Logo, a soma ainda satisfaz as condições do conjunto.

Passo 4

Último passo gente!

λ ∈ R ,   p x ∈ S ⇒ λ p x ∈ S ?

Sim, pois

λ p - 1 = λ p - 1 = λ ∙ 0 = 0 ,   ∀ λ ∈ R

E, tembém

λ p 1 = λ p 1 = λ ∙ 0 = 0 ,   ∀ λ ∈ R

Como satisfez as três condições do teorema, S é um subespaço de P 3

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

No problema, é apresentado um subconjunto de R 2 . Verificar se é um subespaço vetorial do R 2 , relativamente às operações de adição e multiplicação por escalar usuais. S = { x , y ,y = - x }
b. {B in M_n n| A B != B A } .
1.2.4. Seja A uma matriz n × n fixada. Determine se os conjuntos dados são ou não espaços vetoriais.a. B ∈ M n nA B = B A } .
Quais dos seguintes conjuntos de vetores geram o R 4 ? a. 1,0 , 0,1 , 0,1 , 0,0 , 1,1 , 1,1 , 1,1 , 1,0 ;
No problema, é apresentado um subconjunto de R 3 . Verificar se é subespaço em relação às operações de adição e multiplicação por escalar usuais. Se for subespaço, mostrar que as duas condições estão