Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 17.Exercício - Ex. 4b
Determine , projeção ortogonal do ponto sobre a reta , nos casos
é o ortocentro do triângulo de vértices , e e é a reta determinada por e .
Passo 1
O problema quer que achemos a projeção ortogonal de sobre a reta . O problema é que aqui não temos nem o ponto nem a reta ...
Vamos olhar primeiro para a reta. Ela deve passar nos pontos e , de modo que seu vetor diretor é
Assim, uma equação vetorial para ela é
Passo 2
Agora vamos procurar o ponto que é o ortocentro do triângulo de vértices , e . Vale lembrar que o ortocentro é o encontro das alturas de um triângulo:
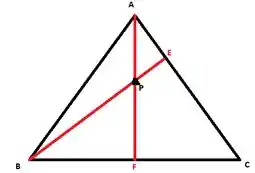
Assim, temos que achar as equações das retas e e, daí, procurar sua interseção. O ponto é a projeção ortogonal de sobre a reta , cujo vetor diretor é
Por simplicidade, vamos usar , de modo que uma equação para a reta é
Assim, o ponto é do tipo
Para que seja a projeção ortogonal de sobre , devemos ter . Assim, como
Temos que
Logo,
Passo 3
Vamos seguir o mesmo raciocínio para achar , que será a projeção ortogonal de sobre . O vetor diretor da reta é
Assim, a equação da reta é
Como o ponto está nessa reta, ele é do tipo
Devemos ter . Como
Temos
Logo,
Portanto,
Passo 4
Agora vamos achar as retas e . Primeiro a reta :
Assim, a equação da reta é
Já para a reta :
Portanto, uma equação para essa reta é
Como queremos achar o ponto de encontro das retas, igualamos as equações:
Assim,
Da primeira equação:
Substituindo na segunda:
Assim, o ponto de encotro das retas é
Esse é o ortocentro!
Passo 5
Agora finalmente podemos terminar o problema: queremos achar a projeção de sobre a reta de equação
O ponto procurado está sobre a reta, de modo que ele deve ser da forma
Para que ele seja a projeção ortogonal de , devemos ter
Como , temos
Portanto,
Logo,