Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 25.Exercício - Ex. 42a
Prove, em cada caso, que a equação dada descreve uma quádrica cônica.
(a)
Passo 1
Bom pessoal, o que significa provar que uma equação descreve uma quádrica cônica?
A forma mais fácil de conseguir isso, é mostrando que a equação pode ser descrita nessa forma aqui:
Então vamos olhar para a nossa equação:
A primeira coisa a fazer é se livrar desses termos lineares. Podemos fazer isso usando o método de completar quadrados.
Passo 2
Começando pelos termos que envolvem :
Isso é muito parecido com esse produto notável aqui:
Então se a gente somar dos dois lados da equação:
Para os termos que envolvem :
Então somando dos dois lados:
E para o :
Então somando dos dois lados:
Ok, já melhorou bastante.
Passo 3
Para chegarmos na forma reduzida lá de cima, vamos reorganizar a equação:
E agora podemos fazer uma translação de coordenadas bastante simples:
Então:
Para ficar mais parecido ainda com a forma geral, vamos fazer uma rotação para trocar o pelo :
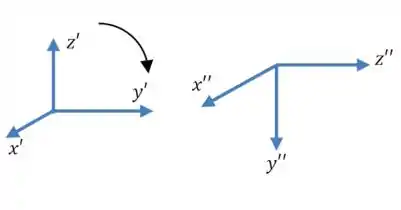
Então:
Substituindo isso na equação:
Agora sim, estamos exatamente na forma reduzia lá de cima, no caso , que é uma quádrica cônica de rotação.
Resposta
Demonstração. A equação do enunciado pode ser reescrita como .