Posições Relativas de Retas
Produzido por Aline BuzziTeoria
Introdução
Olha para a figura abaixo:
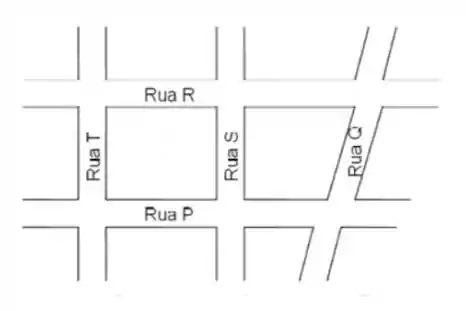
Costumamos falar a Rua R é transversal a Rua S, também que a Rua T é paralela a Rua S. As ruas estão representadas por retas, e podemos compará-las de acordo com as posições entre elas. Se falarmos da posição entre retas, quais as posições possíveis??
Por exemplo: qual a posição relativa entre as retas e dadas abaixo?
Bateu o desespero? Relaxa Aí!!! Vamos te ensinar como faz!!
![]()
Posição Relativa
A posição entre duas retas nada mais é do que a posição que uma reta está em relação à outra.
Mas como assim??
Primeiro, temos 4 posições possíveis entre retas:
- Reversas - São retas que NÃO possuem nenhum ponto em comum e não são paralelas entre si.
- Concorrentes - São retas que possuem um ponto em comum.
- Paralelas Distintas - São retas paralelas, sem nenhum ponto em comum.
- Paralelas Coincidentes (ou iguais) - São retas paralelas que possuem todos os pontos em comum.
- Se , ou seja, forem proporcionais, então significa que as retas são paralelas. Para verificar se são distintas ou iguais basta testar se o ponto de pertence à também. Se pertencer a e são iguais, se não, são distintas.
- Se , então elas são concorrentes.
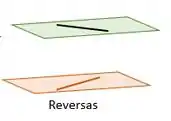
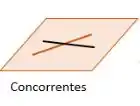
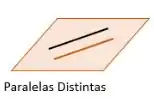
Agora que já sabemos as possíveis posições entre retas, vamos estudar como identificar cada uma das posições!! Dependendo da equação das retas, elas vão estar em uma dessas 4 posições entendeu?
Vamos para um exemplo
As retas e , possuem o vetor diretor e , respectivamente e o ponto pertence a reta e o ponto pertencente à reta . Podemos fazer um desenho para nos auxiliar:
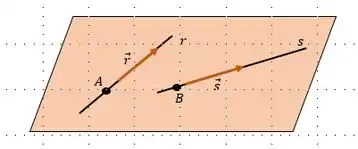
Ok, a primeira coisa que precisamos saber é se essas retas são coplanares ou não.
Se as retas não forem coplanares significa que estão em planos diferentes e que são reversas. Caso as retas forem coplanares então restam três opções, serão: retas paralelas distintas, paralelas coincidentes ou concorrentes.
Como descobrir se as retas são coplanares ou não?
Vamos analisar os vetores diretores de cada reta e também um vetor formado por dois pontos, um de cada reta (no caso do nosso exemplo seria o vetor formado pelos pontos A e B, o vetor). Se os vetores forem LI, as retas e serão reversas (ou seja, nunca irão se cruzar e além disso estão em planos diferentes). Ou seja, se fizermos o produto misto dos vetores e o determinante der DIFERENTE DE ZERO, isso significa que as retas são reversas!!
Voltando para o exemplo:
Então qual a posição relativa das nossas retas e que demos lá no comecinho? Bora, verificar?!
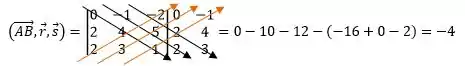
Nossas retas são reversas!!
Ok, mas e se o produto misto der ZERO?!!
Se isso acontecer entramos no caso contrário e as retas são coplanares ou seja, podem ser: retas paralelas distintas, paralelas coincidentes ou concorrentes!! Para decidir qual das 3 é, passaremos a olhar o vetor diretor de cada uma das retas. Vamos supor que os vetores das nossas retas e são, respectivamente, e .
Por exemplo, se liga nessas duas retas no :
Como nossas retas estão no , elas serão concorrentes ou paralelas.
Primeiro vamos achar os vetores diretores e verificar se !
Vou escolher dois pontos aleatórios para reta e , calcular o vetor que liga eles e, assim, teremos os vetores diretores!
Para reta , temos os pontos e . Calculado o vetor , temos
Show de bolinhas! Já temos o nosso !
Vamos fazer para reta agora. Temos os pontos e . Calculando o vetor , temos
Belezinha, nosso vetor diretor é !
Vamos, enfim, verificar se
Se abrirmos isso, ficamos com:
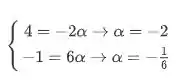
Como os valores de não batem, nossas retas só podem ser CONCORRENTES!! UHULLL
Intersecção de retas
Mas calma, pequeno gafanhoto, já que descobrimos que as retas são concorrentes, eu ainda posso te perguntar em qual ponto, as retas do exemplo anterior, se cruzam (MUAHAHA)!
Bora calcular?! Para fazer isso basta tratar as equações das retas como um sistema e resolver, olha só:
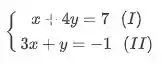
De tiramos que . Substituindo em ,
Substituindo em , temos
Então, o ponto de interseção é !!! Super show de bolinhas!!
Perpendicularidade e Ortogonalidade
No dia a dia, utilizamos os termos perpendicular e ortogonal como sendo a mesma coisa. Será que é isso mesmo ou tem algum detalhe que não levamos em conta?
Há uma diferença, sim!!! Porém, essa diferença só faz sentido quando falamos de retas. Pois, duas retas são perpendiculares quando formam entre si E são concorrentes. Já duas retas ortogonais , formam também o ângulo de e podem ser concorrentes ou reversas.
Dá pra ter uma ideia melhor desses dois conceitos em um cubo, onde todos todos os ângulos são de .
Olhe para esses dois cubos:
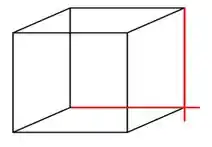
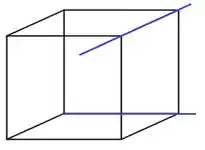
As retas vermelhas são um exemplo de retas perpendiculares, enquanto as azuis são retas ortogonais.
Ok, mas como verificar se as retas são paralelas ou ortogonais?
Assim, primeiro verificamos se duas retas são ortogonais fazendo o produto interno entre os vetores diretores:
Se as retas e são ortogonais para verificar se são perpendiculares basta verificar se as retas possuem algum ponto em comum, ou seja, se são concorrentes.
Ufaa!! A teoria acabou!! Bora praticar?!
![]()
Para saber de cor e salteado tudinho a seguir tem um RESUMÃO IRADO.
RESUMÃO:

Intersecção de retas
Perpendicularidade e Ortogonalidade
Exercícios Resolvidos
Exercício Resolvido #1
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 173-2.
Estude a posição relativa das retas
e
Passo 1
O enunciado nos da a equação vetorial das retas e . Devemos determinar a posição relativa entre as retas.
Dados:
Bora começar a colocar os neurônios para aquecer!! haha

Passo 2
Como vimos na teoria, as retas podem ter 4 posições relativas: reversas, concorrentes, paralelas distintas ou paralelas coincidentes. Para saber se as retas são reversas ou coplanares, basta calcular o produto misto entre os vetores . Mas, sempre que formos avaliar a posição entre duas retas devemos começar avaliando se os vetores das retas são proporcionais. Assim, se forem proporcionais significa que são paralelos. Então, se forem paralelos teremos que analisar se sõ distintos ou iguais. E, se os vetores não forem proporcionais, aí sim faremos o produto misto para decidir se as retas são reversas ou concorrentes. Vamos analisar:
Temos, e , assim:
Portanto, e são paralelos.
Passo 3
Como descobrir se são idênticas ou distintas?
Para saber se são idênticas ou distintas basta testar se um ponto de , por exemplopertence atambém. Assim, vamos testar se o ponto , pertence à . Para isso, vamos substituir o ponto na equação vetorial da reta :
Igualando coordenada a coordenada, temos:
Portanto, o ponto pertence à reta também. Assim, e são paralelas coincidentes (iguais)
Resposta
Exercício Resolvido #2
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 196-1.
Verifique se as retas
são ortogonais. Verifique também se são perpendiculares.
Passo 1
Temos novamente a equação vetorial de duas retas. Mas, agora queremos saber se as retas são ortogonais e se forem, se são perpendiculares também. Vamos retirar então o que temos de informação sobre cada reta:
Dados:
Passo 2
Como vimos na teoria, para verificar se duas retas são ortogonais temos que verificar se o produto interno entre elas é ZERO.
Como o produto interno deu ZERO, então as retas são ortogonais. Será que são perpendiculares também?! Vamos verificar!!
Passo 3
Para saber se duas retas são perpendiculares, precisamos verificar se elas são concorrentes, ou seja, possuem um ponto em comum. Assim, temos duas possibilidades: Ver se as retas são concorrentes ou verificar se possuem um ponto em comum. Vamos fazer pelos dois jeitos.
Vamos começar verificando se são concorrentes!!
Analisando os vetores diretores das retas, vemos que e não são proporcionais. Assim, as retas não são paralelas. Mas, elas podem ser concorrentes ou reversas. Assim, vamos montar o produto misto para verificar isso:
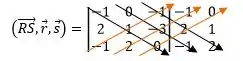
Como o produto misto deu DIFERENTE DE ZERO, então as retas são reversas. Logo, não são perpendiculares.
Passo 4
Outra maneira de verificar a perpendicularidade é ver se as retas possuem algum ponto em comum. Para isso, vamos igualar as coordenadas das retas para ver se encontramos algum ponto possível:
Igualando teremos:
Pelo , chega-se que . Substituindo esse valor na equação de , temos:
Já temos os valores de e . Só falta testar se esses valores também satisfazer a equação do :
Os valores não satisfazem. Assim, as retas não possuem nenhum ponto em comum. Logo, não são perpendiculares.
Resposta
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 136-18.
Calcular o valor de para que os seguintes pares de retas sejam paralelas:
- e
- e
Passo 1
O enunciado nos pede para determinar o valor de para que as retas sejam paralelas. Para isso, devemos garantir que os vetores diretores das retas sejam proporcionais, ou seja:
Passo 2
- Vamos retirar das equações que nos foram dadas o vetor diretor de cada reta:
- Retirando os valores das coordenadas do vetores diretores das retas e , temos:
Agora vamos igualar os vetores à , teremos:
Igualando coordenada a coordenada:
Como todas as equações são coerentes,o valor de para que as retas sejam paralelas é .
Passo 3
Agora, é só igualar à:
Igualando as coordenadas, temos:
Prontinho!!! Você tirou de letra mais um exercício!!

Se tiveres dúvida de onde tirei os vetores das equações das retas, volte um pouquinho na teoria sobre o “Estudo da Reta” ;).
Resposta
Exercício Resolvido #4
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 120-4.
Calcular o valor de para que as retas
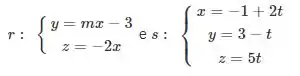
Sejam ortogonais.
Passo 1
Esse exercício também quer saber o valor de .
Devemos achar , mas agora para que as retas sejam ORTOGONAIS. Para que elas sejam ortogonais o produto interno entre os vetores diretores das retas deve ser ZERO, então:
Passo 2
Primeiro, vamos retirar das equações que nos foram dadas o vetor diretor de cada reta. Para retirar o vetor diretor da reta será um pouco mais chatinho, pois ela está no formato reduzido. Mas, não se desespere!! Vamos, com calma!!
Como ela está no formato reduzido, sabemos que um ponto genérico da reta pode ser escrito da seguinte forma:
Como para determinar um vetor precisamos de dois pontos, então escolhemos dois pontos aleatórios:
Sabendo que esses dois pontos pertencem à reta , podemos encontrar o vetor diretor da reta:
O vetor diretor da reta é mais fácil saber, pois temos as equações paramétricas da reta, então o vetor diretor fica explícito na equação:
Passo 3
Agora que já sabemos os vetores diretores é só fazer o produto interno e forçar para que ele dê ZERO para que sejam ortogonais as retas.
Portanto, para as retas serem ortogonais . Logo, o vetor diretor da reta r será:
Resposta
Exercício Resolvido #5
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 198-3.
Ache equações paramétricas da reta que passa por e é perpendicular à reta
Passo 1
Caramba! Só de ler o enunciado bateu o desespero?!
![]()
Respira!! Que essa questão tem alguns detalhes que não falamos ainda!! ;)
Passo 2
Com os dados que temos podemos desenhar nosso problema da seguinte maneira:
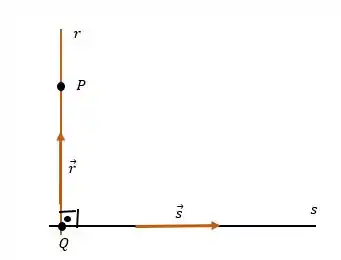
O vetor diretor da reta conseguimos retirar pelas equações simétricas . O ponto é dado, . E a última informação preciosa que temos é que as retas são perpendiculares, ou seja, formam e são concorrentes.
Passo 3
Mas, como acho o vetor diretor da reta ??
Como sabemos que as retas são perpendiculares, então, seus vetores diretores também são. Se são perpendiculares, o produto interno entre eles deve ser ZERO.
O ponto de interseção entre as reta é . Como pertence à reta , então um ponto genérico de é:
Então:
O vetor diretor de será então o vetor formado pleos pontos e :
Assim, se e , temos que fazer o produto interno entre eles e deve dar ZERO.
Resolvendo o produto interno:
Pronto achamos o vetor diretor da reta :
Passo 4
Agora que já temos o vetor diretor e um ponto que pertence à reta , falta escrevermos as equações paramétricas de .
Multiplicando por
Resposta
Exercício Resolvido #6
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 186-1.
Sejam e as retas reversas, passando por e e por e respectivamente. Obtenha uma equação vetorial da reta , concorrente com e , e paralela ao vetor .
Dados: e .
Passo 1
Preparado para mais um exercício sobre posição de retas??

Isso aí!! Nesse exercício vamos utilizar algumas estratégias que ainda não usamos. Então, bora começar!!
Vamos retirar os dados do enunciado:
Dados:
Além disso, e são reversas, ou seja, retas que não são paralelas e não tem ponto em comum.
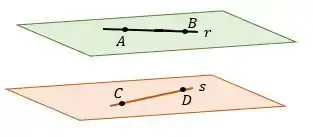
O enunciado disse que é concorrente com e , e paralela ao vetor .
Se é concorrente com e , é porque existe uma ponto comum entre (que chamaremos de ) e um ponto em comum entre (que chamaremos de ). Com esses dados podemos desenhar o seguinte esquema:
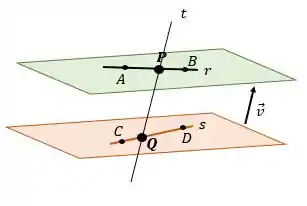
Passo 2
Criamos os pontos e que pertencem a reta , mas não temos nenhuma informação sobre eles. Como também pertence a e também pertence a , para sabermos a cara desses pontos precisamos das equações gerais das retas e .
Vamos começar com a reta :
A e essa reta é formada pelos pontos e podemos escrever que seu vetor diretor é e que o ponto pertencente à reta é . Poderia ter escolhido o vetor como diretor, como o ponto como pertencente à reta. Calculando , podemos escrever a equação geral da reta :
Com a expressão vetorial da reta , podemos escrever o ponto que será da forma:
Beleza?!
Faremos o mesmo para determinar o ponto , mas agora com a reta :
Os pontos e pertence a reta e podemos escolher o vetor diretor e o ponto , para encontrar a equação geral de :
Escolhendo o ponto , Temos que a reta como:
Com a expressão vetorial da reta , podemos escrever o ponto que será da forma:
Pronto!! Temos e . Lembrando que escolhemos e porque são diferentes retas, logo, não podemos usar o mesmo parâmetro.
Passo 3
Agora que temos e , vamos para a segunda parte da resolução!!
Pelo enunciado sabemos que a reta é paralela ao vetor . Se é paralela à , também paralelo ao vetor formado pelos pontos e , Logo temos que é paralelo ao vetor :
Vamos encontrar primeiro o vetor (que será em função de e ):
Substituindo os valores em :
Podemos montar sistema com três equações e três incógnitas e
Isolando na segunda equação temos
Substituindo o valor de na equação e encontrando o valor de :
Tendo , encontramos o valor de :
Substituindo e na equação , temos o valor de :
Chegamos nos três valores:
Agora podemos substituir esses valores para encontrar os pontos e :
Passo 4
Está quase terminando!! Só falta escrevermos a equação vetorial!! Temos o vetor diretor que é e temos dois ponto: e . Escolhendo qualquer um deles, por exemplo, , escrevemos a equação vetorial:
Resposta
Exercício Resolvido #7
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª Ed., São Paulo:McGrawHill, 1987, pp.122 - Modificada
Estude a posição relativa das retas:
e
Passo 1
Vamos começar vendo se os vetores diretores são proporcionais!
Do enunciado tiramos os vetores diretores:
Assim, vamos ver se
Abrindo isso,
Como nenhum valor de bate, e não são paralelos!
Passo 2
Agora, vamos checar se as retas são reversas!
Já conhecemos os vetores diretores:
E os respectivos pontos de cada reta são:
Fazendo
Assim conseguimos montar nosso produto misto!
Como o produto misto deu zero, os vetores são coplanares e as retas não são reversas!
Passo 3
As retas não são paralelas (pois ) nem reversas (pois ). Logo, só podem ser concorrentes!
Resposta
Concorrentes!
Exercício Resolvido #8
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª Ed., São Paulo:McGrawHill, 1987, pp.127
Duas retas e coplanares e não paralelas são concorrentes. Consideremos as retas:
e
Determinemos seu ponto de interseção.
Passo 1
Beleza, vamos achar o ponto de interseção!
O ponto de interseção entre duas retas concorrentes é o ÚNICO ponto em que elas se cruzam, ou seja, é o único ponto em que suas coordenadas são iguais! Então, para achar esse ponto, basta igualar as coordenadas das duas retas!
Como em aparece a incógnita e, em , o não aparece, vamos começar eliminando-o da equação de .
Da equação da coordenada de temos que .
Substituindo isso nas equações para as coordenadas e , temos:
Agora é só igualar as equações das coordenadas de cada reta!
Igualando as equações da coordenada :
Substituindo na equação de qualquer uma das retas (vou substituir em , mas tanto faz):
Com isso o ponto de interseção é:
Resposta
Exercício Resolvido #9
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª Ed., São Paulo:McGrawHill, 1987, pp.126 - Modificada
Mostre que as retas abaixo são concorrentes e determine o ponto de interseção entre elas.
e
Passo 1
Como o problema pede para mostrarmos que as retas são concorrentes, vamos mostrar que não são paralelas nem reversas.
Do enunciado tiramos os vetores diretores:
Assim, vamos ver se
Abrindo isso,
Como nenhum valor de bate, e não são paralelos!
Agora, vamos checar se as retas são reversas!
Já conhecemos os vetores diretores:
E os respectivos pontos de cada reta são:
Fazendo
Assim conseguimos montar nosso produto misto!
Como o produto misto deu zero, os vetores são coplanares e as retas não são reversas!
Logo, só podem ser concorrentes 😊
Passo 2
Beleza, vamos achar o ponto de interseção agora!
Para facilitar a nossa visualização, vou passar a equação de para forma paramétrica:
a gente já conhece:
O ponto de interseção entre duas retas concorrentes é o ÚNICO ponto em que elas se cruzam, ou seja, é o único ponto em que suas coordenadas são iguais! Então, para achar esse ponto, basta igualar as coordenadas das duas retas! Temos os sistemas:
Somando as duas primeiras equações:
Substituindo nas 3 equações:
Beleza, o deu igual em todas (ufa!). Agora podemos achar o ponto!
Passo 3
Podemos usar qualquer uma das retas. Vou usar a :
Nosso ponto vale então: