Ângulos entre Retas
Produzido por Aline BuzziTeoria
Opa! Bora bater um papo sobre ângulo entre retas?! Então me conta, como você faria se eu te pedisse pra calcular o ângulo
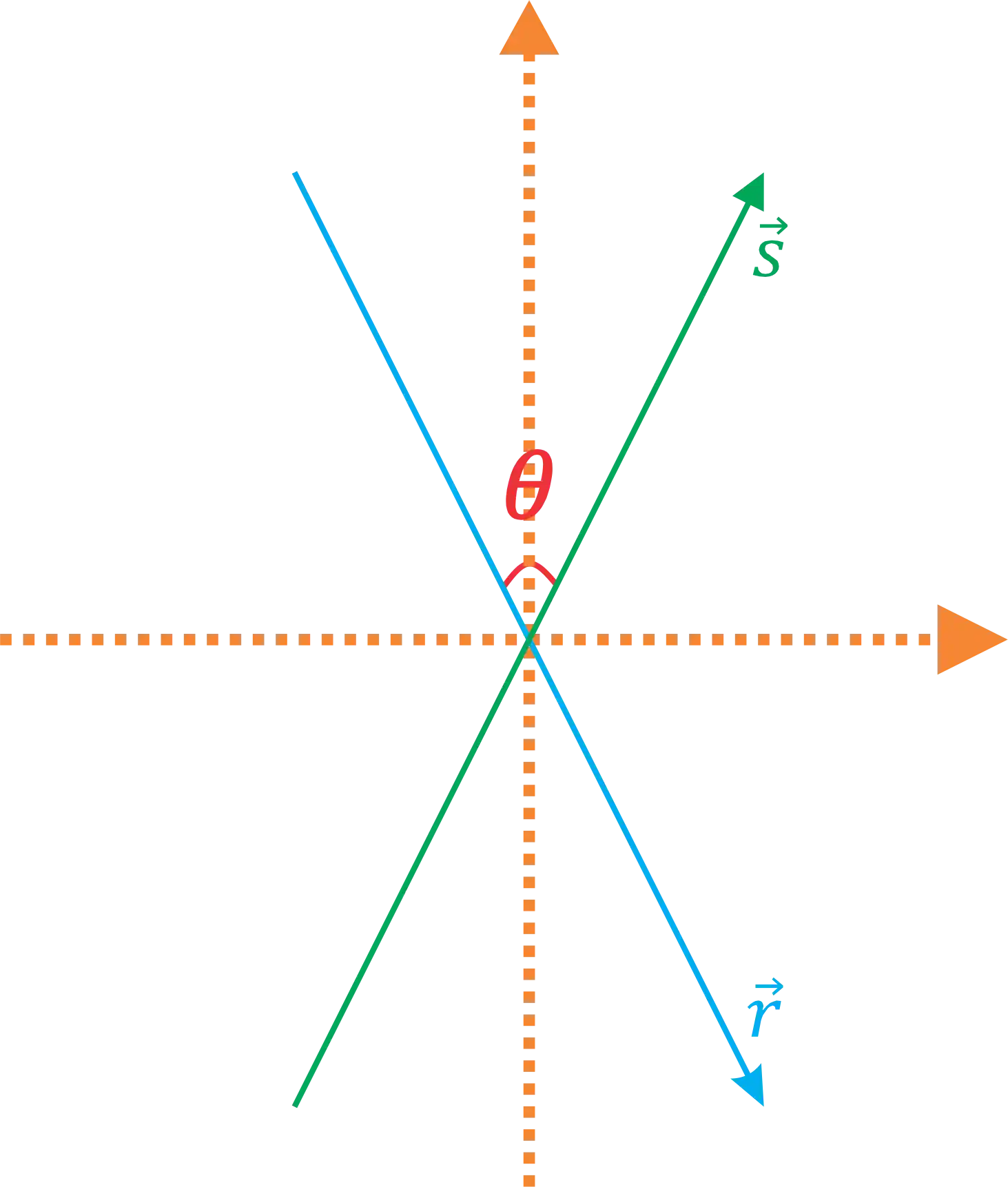
Pra começar com tudo, dá uma conferida nesse vídeo abaixo que eu te explico como calcular o ângulo
📢 Clique para ver mais:
- Ângulo Entre Retas: Exercícios Resolvidos
- Equações Paramétricas
- Posições Relativas de Retas
- Introdução à Reta
Ou então, continua comigo no textinho! 👇
Como Calcular o Ângulo entre Duas Retas?
Para calcularmos um ângulo
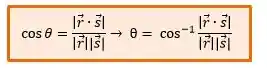
Onde
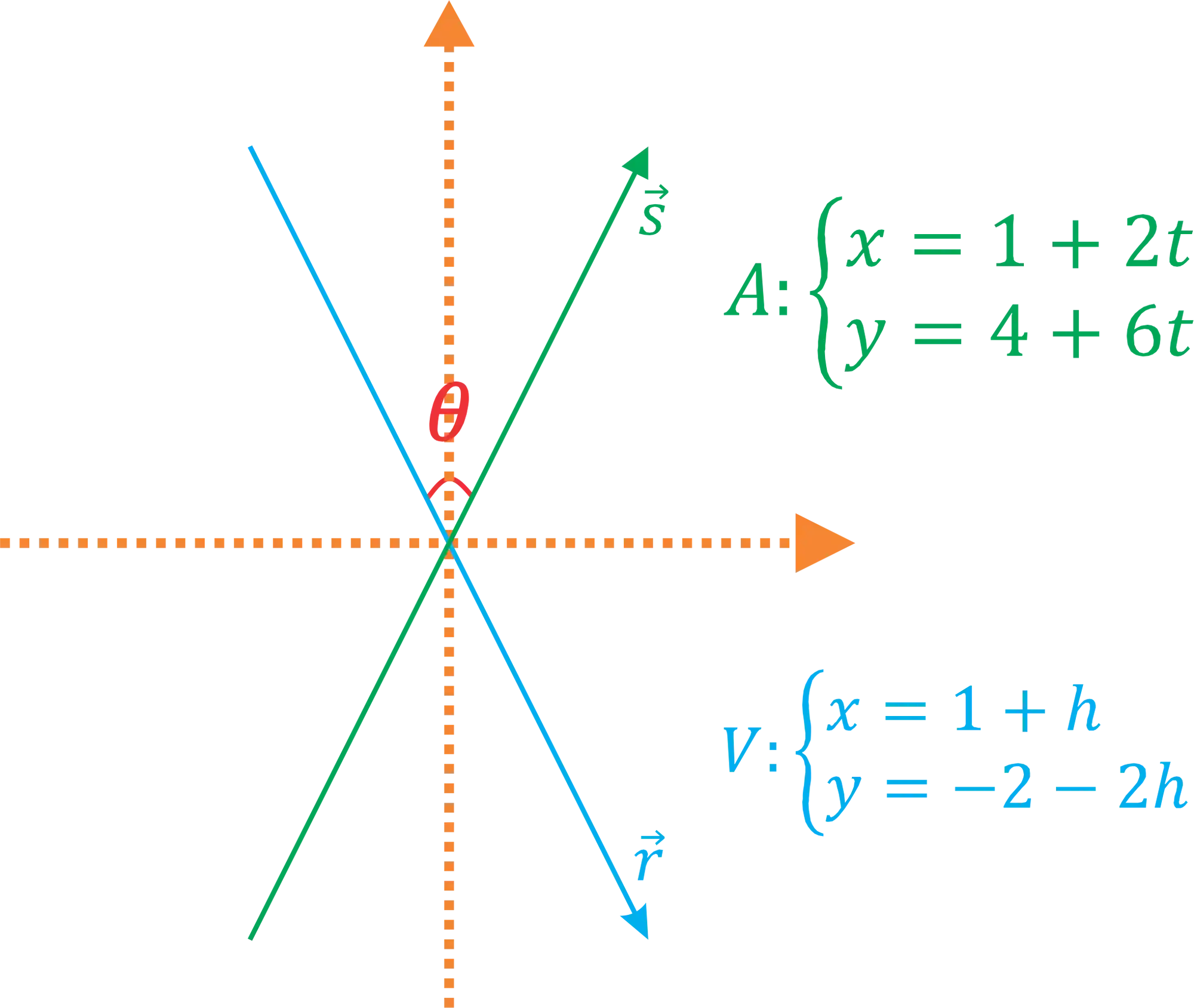
Passo 1: Identificar os Vetores Diretores
Na figura acima temos as equações paramétricas dos vetores, podemos então escrever os vetores diretores:
Passo 2: Calcular o Produto Interno
Vamos calcular o produto interno
Passo 3: Substituir na Fórmula
Agora vamos substituir nossos dados na fórmula:
Prontinho! Agora vamos praticar com exercícios?