Combinação e Dependência Lineares
Produzido por Aline BuzziTeoria
Galera, esses dois conceitos são super hiper importantes, então se liguem neles!
Felizmente, são tranquilinhos de entender também 😊
Combinação Linear
Lá em “Operações com Vetores” falamos um pouco sobre esse assunto, mas se você não lembra pode ficar tranks que agora vou explicar tudo tim tim por tim tim!
Uma combinação linear nada mais é do que uma soma de vetores, ou seja, é como se eu pegasse um vetor e escrevesse ele em função de outros vetores. Vamos ver um exemplo!
Imaginem que queremos escrever em função de e de .
Precisamos arrumar um jeito de, somando e , chegar em . Então, vamos escrever uma expressão genérica para isso:
Agora só precisamos descobrir quem são e !
Substituindo nossos vetores,
Abrindo essa expressão:
De , . Substituindo em , temos
Achamos nossos coeficientes!!! Vamos ver se eles batem substituindo-os em
UHULL, deu certo!
Reparem que, de fato
E o que acabamos de fazer pode ser representado pela figura abaixo
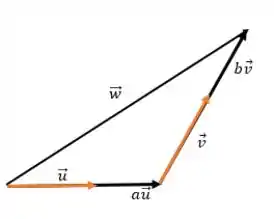
Vamos fazer um último exemplinho!
O vetor é dos vetores , e ?
Escrevendo a expressão genérica,
Abrindo a expressão:
De tiramos que . Substituindo em :
Substituindo e em :
Agora é só achar e !
Vamos substituir na nossa expressão original
Dependência Linear
Esse conceito tem tudo a ver com , então vamos aproveitar que ainda tá fresco na cabeça e seguir em frente!
Para gente saber se um conjunto de vetores é linearmente dependente (LD) ou linearmente independente (LI) é só ver se algum desses vetores é combinação linear dos demais. Se for uma combinação linear, o conjunto é LD. Caso contrário, o conjunto é LI!
Tá boiando ainda? Vamos dar uma olhada em um exemplo para você entender tudinho!
Se liga nesse conjunto de vetores:
Será que fazendo alguma , conseguimos gerar o vetor nulo? Vamos tentar equacionar isso:
Montando o sistema:
Podemos ver que e por consequência .
Logo só existe um único jeito de gerar o vetor nulo, que é e e essa é a solução trivial! Quando o ÚNICO jeito de gerar o vetor nulo for com todos os coeficientes iguais a zero, o conjunto é !
Tá, mas e quando não acontece isso? A gente vai chamar o conjunto de vetores de Linearmente dependente ou LD para os íntimos.
Beleza, agora vamos fazer alguns exemplos.
Exemplo: O conjunto é ou ?
Vamos aplicar a definição:
Como podemos ver, utilizando a definição, sempre acaba num sistema linear ai basta resolver ele e achar valores para os coeficientes. No caso, achamos que , ou seja, os coeficientes são sempre !! E de acordo com a definição, os vetores são , pois os coeficientes são todos nulos.
Exemplo: o conjunto é ou ?
Vamos equacionar!
Igualando os vetores e montando o sistema:
Se fizermos , temos:
Ainda não terminou, temos que substituir em alguma das outras equações para ver as relações com o coeficiente , afinal tudo tem que estar em função de uma mesma constante. Vamos substituir na :
Tá, então achamos que:
Que resposta confusa! O que isso quer dizer?
Isso significa que se pegarmos e e substituirmos em , teremos sempre o vetor nulo. Olha só:
Então, se, por exemplo, , basta que . Assim, nossa equação ficaria:
Mas poderíamos multiplicar a equação por qualquer constante! Como, por exemplo, por 3:
Logo, temos infinitas possibilidades de gerar o vetor nulo! Isso quer dizer que o nosso conjunto é .
Métodos práticos
Pô, meio complicado esse último exemplo, não? É verdade, existem jeitos mais práticos de ver se um conjunto é ou . Um deles é o fato abaixo:
Fato: Um conjunto de vetores é se, e somente se, algum dos seus vetores é dos demais.
Assim, no exemplo anterior bastava olha que:
E pronto, o conjunto é .
Existem dois métodos práticos que vão nos ajudar muito a verificar se um conjunto de vetores é ou .
- Verificar no olho qual vetor é dos demais. OBS: normalmente é o jeito mais rápido.
- Verificar os zeros nas coordenadas dos vetores.
Esses dois usam o fato que acabei de mencionar acima, pois se você já descobrir quem é dos demais então já podemos dizer que o conjunto é . Se não conseguir achar nenhum vetor assim, então o conjunto é .
Exemplo: O conjunto é ou ?
Podemos ver que:
Então, o terceiro vetor é uma dos demais e o conjunto é .
Exemplo: O conjunto é ou ?
Aí vai uma dica. Repara que tem o vetor nulo né? Vamos usar a definição:
Agora você vai e pensa, ahhh então todos os coeficientes são zero, logo o conjunto é .

Vê ali em cima, que o multiplicou o vetor nulo, quando a gente somou ele sumiu, MAS ISSO NÃO QUER DIZER QUE ELE É ZERO! Quer dizer que ele é qualquer coisa, então temos infinitas possibilidades para E POR ISSO O CONJUNTO É !
Então sempre que tiver o vetor nulo ele será , porque vai sempre acontecer a mesma coisa que fizemos ali em cima.
A teoria fica por aqui!

Só falta dar uma olhada nos exercícios para ficar tudo show de bolinhas!!!