Produto Escalar
Produzido por Aline BuzziTeoria
Opaaa! Bora bater um papo sobre Produto Escalar?
O que é o Produto Escalar?
O produto escalar é a multiplicação entre dois VETORES e tem como resultado um ESCALAR! Ele também é conhecido como produto interno usual!
-Mas como assim?! 😖
Imagina esses dois vetores aqui:
A forma com o "pontinho"
📢 Clique para ver mais:
Como Calcular o Produto Escalar
O cálculo do produto escalar é bem simples! Tudo o que temos que fazer é multiplicar as coordenadas equivalentes e depois somar com as demais.
Assim:
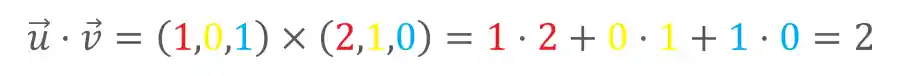
Viu? Agora entendeu porque multiplicamos dois vetores e obtemos um escalar como resposta?
Mas, não acaba por aqui, existe uma outra fórmula de calcular o produto escalar, que usa o módulo dos vetores e o ângulo entre eles:
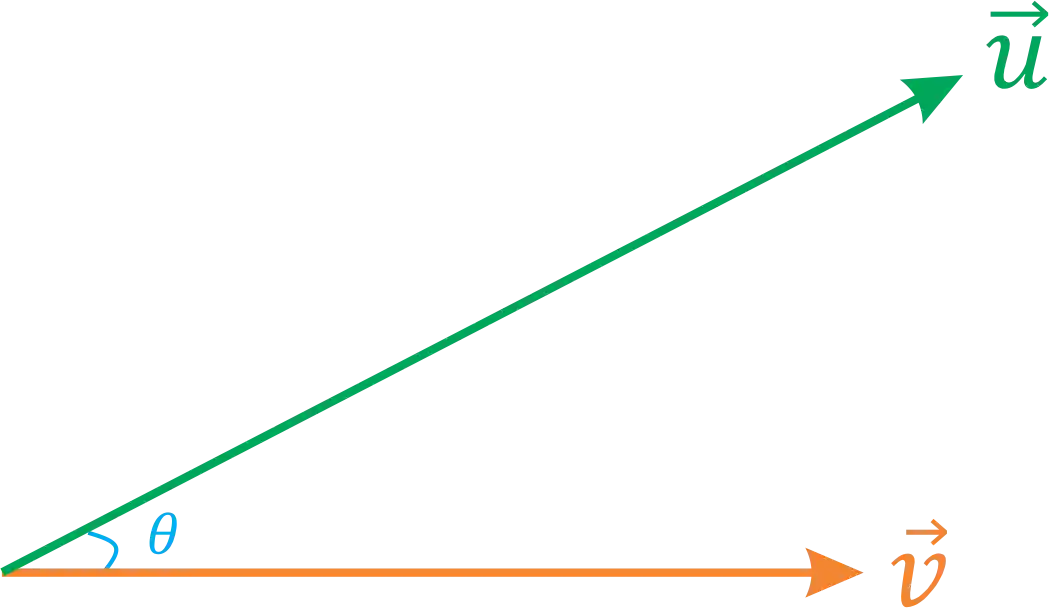
Nesse caso usamos essa fórmula aqui:
Por essa segunda fórmula a gente consegue perceber uma coisa BEM IMPORTANTE: "O produto escalar entre dois vetores ortogonais (formam um ângulo de 90°) é ZERO"
Você também pode conferir esse conteúdo em vídeo, aqui em baixo:
Propriedades do Produto Escalar
O produto escalar como qualquer outra operação possui algumas propriedades. Bora ver elas?
Comutativa
A propriedade comutativa diz que, no produto escalar, a ordem dos fatores não alteram o produto. Assim:
Distributiva
Segundo a propriedade distributiva, temos:
Módulo
O módulo de um vetor pode ser calculado a partir da seguinte fórmula:
Exemplo: Calcule o Produto Escalar entre os vetores
Como terminamos de ver, não existe mistério na hora de calcular o produto escalar! A gente vai multiplicar as coordenadas correspondes, uma a uma e depois somar tudo. Assim:
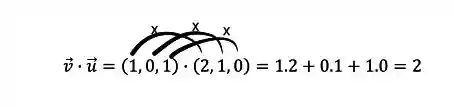
Dessa forma o produto escalar entre os vetores