a) Encontre a solução geral do PVI
b) Faça o gráfico das soluções em função do tempo e discuta o comportamento do sistema conforme .
Passo 1
a) Cara, esse é um sistema homogêneo. A solução dele tem a cara:
O que a gente precisa fazer é calcular e . Isso é uma questão para a gente resolver usando o cálculo funcional. Bora!
A gente precisa começar achando os autovalores de , que é a matriz que aparece no sistema
Vamos usar a equação
Onde é a matriz identidade. Substituindo as coisinhas que a gente tem:
Calculando esse determinante:
Resolvendo essa equação de segundo grau, achamos
Passo 2
Como nossos dois autovalores são iguais e reais, vamos resolver esse sistema para achar e :
Temos já de cara que
Substituindo na primeira:
Passo 3
Agora é montar a nossa solução:
Onde é a matriz identidade. Aí fica:
Passo 4
Vamos aplicar
Em
Daí
Nossa solução fica:
Uhul! Arrasamos!
Passo 5
b) Vamos calcular
As componentes explodem para mais e para menos infinito.
Ele pediu também para esboçarmos e . Essas duas curvas vão ter formatos parecidos.
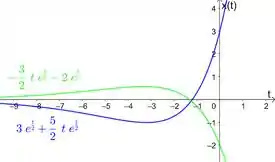
Para esboçar elas, a gente lembra como é o esboço de uma solução do tipo , com . E leva em consideração o resultado dos nossos limites. Fica assim:
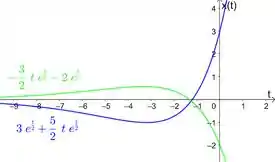
Repara que a verdinha é e explode para menos infinito, e a azul é a que explode para mais infinito.
Arrasamos!
Resposta
a)
b)