Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Forma de Lagrange

Ver Todos os Exercícios

Teoria

Introdução

Falaaaaaa meus jovenzitos, no tópico sobre Interpolação por sistema linear nós vimos um basicão sobre interpolação. Basicamente, quando eram conhecidos apenas valores numéricos da função para um conjunto de pontos e era necessário calcular um ponto não tabelado. Hmmmm... show, um dos métodos mais conhecidos pra resolver esse tipo de situação é usando Interpolação polinomial.

Interpo... o quê??? Era um método que dizia que qualquer função definida e contínua em um intervalo fechado, existe um polinômio que está tãoooooo próximo da função quanto quisermos.

Maaaaaaas, apesar da facilidade de aplicação desse método, ele tem alguns problemas que se devem aos métodos numéricos para a resolução de sistemas lineares. Por exemplo, se tivéssemos pontos muito próximos de zero, já que o sistema linear a ser resolvido seria algo do tipo:

1 0.001 0.002 1 0.003 0.005 1 0.007 0.007 a 0 a 1 a 2 17 - 5 7

Sendo assim, precisamos de métodos mais confiáveis para a obtenção da nossa função de interpolação e é aí que entra a forma de Lagrange.

Polinômios Interpoladores de Lagrange

A ideia é parecida com a da interpolação linear. Dá pra fazer isso generalizando o conceito de interpolação linear. Veja bem, vamos montar um polinômio de grau n (onde a maiooooooor potência de x será n ) que vai interpolar nossa função f x nos pontos x 0 ,   x 1   e   x n . Os coeficientes a k de p n x devem ser tais que:

f x k =   p n x k

Definiremos as funções L i   ( x k ) com a seguinte propriedade:

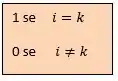
Nosso objetivo nesse método é escrever nosso polinômio p n x como combinação de polinômios L 0 ,   L 1 ,   … ,   L n de grau n . Assim oh:

p n x = y 0 L 0 x + y 1 L 1 x + … + y n L n x

onde y i = f x i .

Para que p n x i = f x i = y i definimos os polinômios L k como:

L k x = x - x 0 x - x 1 … x - x k - 1 x - x k + 1 … x - x n x k - x 0 x k - x 1 … x k - x k - 1 x k - x k + 1 … x k - x n

Veja bem, se: x 0 ,   x 1 … x n são diferentes e a f ( x ) é uma função de valores são dados esses números. Então existe um ÚNICO POLINÔMIO DE GRAU MÁXIMO N.

p n x i = f x i

Meio confuso? Vamos ver um exemplo para ficar melhor, pode ser? Determine o polinômio interpolador para os pontos:

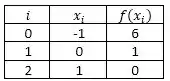
Primeiro: Analisar o número de i presentes na função dada. No caso temos três pontos i = 0,1   e   2 . Isso significa que temos TRÊS NÓS, mas o grau do polinômio é 2. Então uma regrinha legal de marcar é que o grau de polinômio sempre vai ser n ú m e r o   t o t a l   d e   p o n t o s   - 1 , ou seja, se temos n pontos, o polinômio será de grau n - 1 .

Como temos 3 nós de interpolação, nosso polinômio será de grau 2 . E definindo x 0 = - 1 ,   x 1 = 0 e x 2 = 1 , temos:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

Onde:

y 0 = f x 0 = 6

y 1 = f x 1 = 1

y 2 = f x 2 = 0

Segundo: a PRÓXIMA coisa importante para se fazer é analisar que termos nós temos e como montar os interpoladores de Lagrange. Seguindo a fórmula geral:

L k x = x - x 0 x - x 1 … x - x k - 1 x - x k + 1 … x - x n x k - x 0 x k - x 1 … x k - x k - 1 x k - x k + 1 … x k - x n

Veja bem, nós temos nesse caso :   x 0 ,   x 1   e   x n = x 2 . Isso significa que temos que montar L 0 ,   L 1   e   L 2 . Um bom macete pra montar essa estrutura é:

Quem manda no L 0 é o grau 0, então x 0 fica no quociente e manda sempre subtrair os outros termos. E ele nuuuuuunca vai aparecer em cima. Já os outros 2 pontos ( x 1 e   x 2 ) aparecem em cima e embaixo. Fica assim:

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 0 x - 1 - 1 - 0 - 1 - 1 = x 2 - x 2

Quem manda no L 1 é o grau 1, então x 1 fica no quociente e manda sempre subtrair os outros termos. E ele nuuuuuunca vai aparecer em cima. Já os outros 2( x 0 e   x 2 ) aparecem em cima e embaixo. Fica assim:

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - - 1 x - 1 0 - - 1 0 - 1 = ( x + 1 ) ( x - 1 ) - 1 = x 2 - 1 - 1

Quem manda no L 2 é o grau 2, então x 2 fica no quociente e manda sempre subtrair os outros termos. E ele nuuuuuunca vai aparecer em cima. Já os outros 2( x 0 e   x 1 ) aparecem em cima e embaixo. Fica assim:

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - - 1 x - 0 1 - - 1 1 - 0 = x 2 + x 2

Terceiro: Agora juntamos tudo no polinômio:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

p 2 x = 6 x 2 - x 2 + 1 . x 2 - 1 - 1 + 0 x 2 + x 2 =   2 x 2 - 3 x + 1

Olha como ficam essas coisas todos no gráfico. Os pontos são:

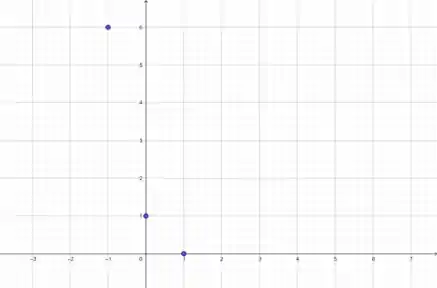
E o polinômio que achamos fica:

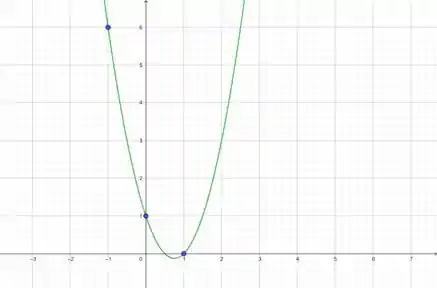
Não é fácil, nem difícil. Mas se fizer com calma e paciência fica bem automático pra responder né?

O chato aqui é que à medida que aumentamos o grau de p n nós não só precisamos calcular mais polinômios L i como eles também se tornam mais trabalhosos de se calcular. Fora que o cálculo final de p n x também vai ficando cada vez mais chato à medida que aumentamos o grau do nosso polinômio interpolador.

Algoritmo

Agora nosso algoritmo vai sofrer uma mudança haha. Vamos lá:

Passo 1. Dados iniciais (o que seu programa vai receber de você):

a. Vetor de valores x = x 0 , x 1 , … , x n

b. Vetor de valores f x = f x 0 , f x 1 , … , f x n

c. Valor x - onde se quer avaliar f x

Passo 2. Para i de 0 a n faça os passos de 3 a 4:

Passo 3. L i = 1

Passo 4. Para j de 0 a n faça o passo 5:

Passo 5. Se j ≠ i : L i = L i ∙ x - - x j x i - x j

Passo 6. Nossa aproximação para f x ¯ será o valor y 0 L 0 + y 1 L 1 + … + y n L n

Como nosso objetivo final em geral é aproximar f x em algum ponto x ¯ , o algoritmo já calcula diretamente o valor de p n x nesse ponto x ¯ ao invés de nos dar a função de interpolação (o que seria bem mais trabalhoso).

Algoritmo

Exercícios Resolvidos

Exercício Resolvido #1

Lista 4 – Professora Angela – UFRJ – Questão 1

Dada a tabela da população de uma vila no início de cada ano, estimar a população em setembro de 1972, usando o polinômio de Lagrange de grau 2 .

Passo 1

Vamos encontrar uma função de interpolação através do método de lagrange. Para isso vamos relacionar a população como (y) e o ano com (x). Ele quer um polinômio de Lagrange de grau 2 , então precisamos de 3 pontos. Os anos mais próximos de setembro de 1972 são:

x 0 = 1972

x 1 = 1973

x 2 = 1974

E temos:

y 0 = 6600

y 1 = 7200

y 2 = 8000

Nosso p 2 x será da forma:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

Passo 2

Calculando os polinômios L k :

L k x = x - x 0 x - x 1 … x - x k - 1 x - x k + 1 … x - x n x k - x 0 x k - x 1 … x k - x k - 1 x k - x k + 1 … x k - x n

Primeiro o L 0 , como

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 1973 x - 1974 1972 - 1973 1972 - 1974 = x 2 - 3947 x + 3894702 2

Agora para os outros polinômios:

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 1972 x - 1974 1973 - 1972 1973 - 1974 = - x 2 + 3946 x - 3892728

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 1972 x - 1973 1974 - 1972 1974 - 1973 = x 2 - 3945 x + 3890756 2

Passo 3

Jogando tudo na fórmula:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

p 2 x = 6600 x 2 - 3947 x + 3894702 2 + 7200 - x 2 + 3946 x - 3892728 + 8000 x 2 - 3945 x + 3890756 2

p 2 x = 100 x 2 - 393900 x + 387899000

Agora tem que tomar cuidado com uma coisa. Nós usamos a população do começo de cada ano para fazer essa aproximação. Mas ele pede a população em setembro de 1972! Então como fazemos isso? Bom, o ano tem 12 meses (que seria 100%) então cada mês corresponde a 100 % 12 = 8,3333 % do ano. Setembro é o 9° mês do ano que corresponde a 8,3333 % × 9 = 75 %   no ano. Se considerarmos o mês como sendo uma parte decimal do ano teremos que do inicio do ano até setembro de 1972 equivale ao ano 1972 + 0,75 = 1972,75 . Substituindo esse valor na nossa função de interpolação:

p 2 1972.75 = 7031.25

Logo, temos aproximadamente 7031 pessoas nessa vila em setembro de 1972.

Resposta

A população desta vila em setembro de 1972 é de aproximadamente 7031 pessoas.

Exercício Resolvido #2

Lista 4 – Professor Mauro – UFRJ – Questão 8 adaptada

A tabela abaixo representa a inflação bimestral medida pelo I N P C no ano de 2000 .

Estime qual foi a inflação em abril, utilizando o polinômio de Lagrange de grau n ≤ 2 .

Passo 1

Para encontrarmos o polinômio de Lagrange de grau 2 precisamos de 3 pontos. Como queremos estimar a inflação em abril, vamos pegar os meses mais próximos dele. E os meses mais próximos de abril são:

x 0 = f e v e r e i r o = 2

x 1 = m a r ç o = 3

x 2 = m a i o = 5

E temos:

y 0 = 0.64

y 1 = 0.24

y 2 = 2.94

Nosso p 2 x será da forma:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

Passo 2

Calculando os polinômios L i :

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 3 x - 5 2 - 3 2 - 5 = x 2 - 8 x + 15 3

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 2 x - 5 3 - 2 3 - 5 = - x 2 + 7 x - 10 2

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 2 x - 3 5 - 2 5 - 3 = x 2 - 5 x + 6 6

Passo 3

Jogando tudo na fórmula:

p 2 x = 175 x 2 - 995 x + 1482 300

Substituindo 4 no nosso polinômio que seria o valor de abril temos:

p 2 4 = 1.00667

Resposta

A partir das informações dadas podemos estimar que a inflação em abril foi de aproximadamente 1.00667 .

Exercício Resolvido #3

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 115, exercício 2 adaptada.

Para as funções f x abaixo, sejam x 0 = 1 , x 1 = 1.25 e x 2 = 1.6 . Encontre funções de interpolação de grau 1 e 2 para aproximar f 1.4 e encontre o erro absoluto.

a f x = sin ⁡ π x

b f x = x - 1 3

c f x = log 10 ⁡ 3 x - 1

d f x = e 2 x - x

Passo 1

a Para encontrar o polinômio de Lagrange de grau 1 vamos usar os pontos:

x 0 = 1.25

x 1 = 1.6

pois estão mais próximos de 1.4 . Temos então que:

p 1 x = y 0 L 0 + y 1 L 1 ,

onde:

y 0 = sin ⁡ 1.25 π = - 0.70711

y 1 = sin ⁡ 1.6 π = - 0.95106

L 0 = x - x 1 x 0 - x 1 = 1.6 - x 0.35

L 1 = x - x 0 x 1 - x 0 = x - 1.25 0.35

Logo,

p 1 x = 0.16414 - 0.697 x

Substituindo 1.4 no polinômio:

p 1 1.4 = - 0.81166

O valor real da função nesse ponto é:

f 1.4 = sin ⁡ 1.4 π = - 0.95106

E o erro absoluto vale:

E A = p 1 1.4 - f 1.4 = 0.1394

Passo 2

Para encontrar o polinômio de Lagrange de grau 2 vamos usar os pontos:

x 0 = 1

x 1 = 1.25

x 2 = 1.6

Temos então que:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2 ,

onde:

y 0 = sin ⁡ π = 0

y 1 = sin ⁡ 1.25 π = - 0.70711

y 2 = sin ⁡ 1.6 π = - 0.95106

Repare que como o y 0 foi zerado não precisamos nos preocupar em calcular L 0 !

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 1 x - 1.6 1.25 - 1 1.25 - 1.6 = - 11.4286 x 2 + 29.7143 x - 18.2857

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 1 x - 1.25 1.6 - 1 1.6 - 1.25 = 4.7619 x 2 - 10.7143 x + 5.95238

Logo,

p 2 x = 3.55242 x 2 - 10.8213 x + 7.26893

Substituindo 1.4 no polinômio:

p 2 1.4 = - 0.91819

O valor real da função nesse ponto é:

f 1.4 = sin ⁡ 1.4 π = - 0.95106

E o erro absoluto vale:

E A = p 2 1.4 - f 1.4 = 0.03287

Passo 3

b Para encontrar o polinômio de Lagrange de grau 1 vamos usar os pontos:

x 0 = 1.25

x 1 = 1.6

pois estão mais próximos de 1.4 . Temos então que:

p 1 x = y 0 L 0 + y 1 L 1 ,

onde:

y 0 = 1.25 - 1 3 = 0.62996

y 1 = 1.6 - 1 3 = 0.84343

L 0 = x - x 1 x 0 - x 1 = 1.6 - x 0.35

L 1 = x - x 0 x 1 - x 0 = x - 1.25 0.35

Logo,

p 1 x = 0.60991 x - 0.13243

Substituindo 1.4 no polinômio:

p 1 1.4 = 0.72145

O valor real da função nesse ponto é:

f 1.4 = 1.4 - 1 3 = 0.73681

E o erro absoluto vale:

E A = p 1 1.4 - f 1.4 = 0.01536

Passo 4

Para encontrar o polinômio de Lagrange de grau 2 vamos usar os pontos:

x 0 = 1

x 1 = 1.25

x 2 = 1.6

Temos então que:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2 ,

onde:

y 0 = 1 - 1 3 = 0

y 1 = 1.25 - 1 3 = 0.62996

y 2 = 1.6 - 1 3 = 0.84343

Repare que como o y 0 foi zerado não precisamos nos preocupar em calcular L 0 !

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 1 x - 1.6 1.25 - 1 1.25 - 1.6 = - 11.4286 x 2 + 29.7143 x - 18.2857

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 1 x - 1.25 1.6 - 1 1.6 - 1.25 = 4.7619 x 2 - 10.7143 x + 5.95238

Logo,

p 2 x = - 3.18323 x 2 + 9.68206 x - 6.49884

Substituindo 1.4 no polinômio:

p 2 1.4 = 0.8169

O valor real da função nesse ponto é:

f 1.4 = 1.4 - 1 3 = 0.73681

E o erro absoluto vale:

E A = p 2 1.4 - f 1.4 = 0.08009

Passo 5

c Para encontrar o polinômio de Lagrange de grau 1 vamos usar os pontos:

x 0 = 1.25

x 1 = 1.6

pois estão mais próximos de 1.4 . Temos então que:

p 1 x = y 0 L 0 + y 1 L 1 ,

onde:

y 0 = log 10 ⁡ 3.75 - 1 = 0.43933

y 1 = log 10 ⁡ 4.8 - 1 = 0.57978

L 0 = x - x 1 x 0 - x 1 = 1.6 - x 0.35

L 1 = x - x 0 x 1 - x 0 = x - 1.25 0.35

Logo,

p 1 x = 0.40129 x - 0.06228

Substituindo 1.4 no polinômio:

p 1 1.4 = 0.49952

O valor real da função nesse ponto é:

f 1.4 = log 10 ⁡ 4.2 - 1 = 0.50515

E o erro absoluto vale:

E A = p 1 1.4 - f 1.4 = 0.00563

Passo 6

Para encontrar o polinômio de Lagrange de grau 2 vamos usar os pontos:

x 0 = 1

x 1 = 1.25

x 2 = 1.6

Temos então que:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2 ,

onde:

y 0 = log 10 ⁡ 3 - 1 = 0.30103

y 1 = log 10 ⁡ 3.75 - 1 = 0.43933

y 2 = log 10 ⁡ 4.8 - 1 = 0.57978

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 1.25 x - 1.6 1 - 1.25 1 - 1.6 = 6.66667 x 2 - 19 x + 13.33333

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 1 x - 1.6 1.25 - 1 1.25 - 1.6 = - 11.4286 x 2 + 29.7143 x - 18.2857

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 1 x - 1.25 1.6 - 1 1.6 - 1.25 = 4.7619 x 2 - 10.7143 x + 5.95238

Logo,

p 2 x = - 0.25321 x 2 + 1.12288 x - 0.56865

Substituindo 1.4 no polinômio:

p 2 1.4 = 0.50709

O valor real da função nesse ponto é:

f 1.4 = log 10 ⁡ 4.2 - 1 = 0.50515

E o erro absoluto vale:

E A = p 2 1.4 - f 1.4 = 0.00194

Passo 7

d Para encontrar o polinômio de Lagrange de grau 1 vamos usar os pontos:

x 0 = 1.25

x 1 = 1.6

pois estão mais próximos de 1.4 . Temos então que:

p 1 x = y 0 L 0 + y 1 L 1 ,

onde:

y 0 = e 2.5 - 1.25 = 10.93249

y 1 = e 3.2 - 1.6 = 22.93253

L 0 = x - x 1 x 0 - x 1 = 1.6 - x 0.35

L 1 = x - x 0 x 1 - x 0 = x - 1.25 0.35

Logo,

p 1 x = 34.2858 x - 31.9248

Substituindo 1.4 no polinômio:

p 1 1.4 = 16.0753

O valor real da função nesse ponto é:

f 1.4 = e 2.8 - 1.4 = 15.04465

E o erro absoluto vale:

E A = p 1 1.4 - f 1.4 = 1.03065

Passo 8

Para encontrar o polinômio de Lagrange de grau 2 vamos usar os pontos:

x 0 = 1

x 1 = 1.25

x 2 = 1.6

Temos então que:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2 ,

onde:

y 0 = e 2 - 1 = 6.38906

y 1 = e 2.5 - 1.25 = 10.93249

y 2 = e 3.2 - 1.6 = 22.93253

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 1.25 x - 1.6 1 - 1.25 1 - 1.6 = 6.66667 x 2 - 19 x + 13.33333

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 1 x - 1.6 1.25 - 1 1.25 - 1.6 = - 11.4286 x 2 + 29.7143 x - 18.2857

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 1 x - 1.25 1.6 - 1 1.6 - 1.25 = 4.7619 x 2 - 10.7143 x + 5.95238

Logo,

p 2 x = 26.8531 x 2 - 42.2469 x + 21.7823

Substituindo 1.4 no polinômio:

p 2 1.4 = 15.2688

O valor real da função nesse ponto é:

f 1.4 = e 2.8 - 1.4 = 15.04465

E o erro absoluto vale:

E A = p 2 1.4 - f 1.4 = 0.22415

Resposta

a p 1 x = 0.16414 - 0.697 x ; p 1 1.4 = - 0.81166 ; E A = 0.1394

p 2 x = 3.55242 x 2 - 10.8213 x + 7.26893 ; p 2 1.4 = - 0.91819 ; E A = 0.03287

b p 1 x = 0.60991 x - 0.13243 ; p 1 1.4 = 0.72145 ; E A = 0.01536

p 2 x = 1 + 0.48344 x - 0.06987 x 2 ; p 2 1.4 = 0.8169 ; E A = 0.08009

c p 1 x = 0.40129 x - 0.06228 ; p 1 1.4 = 0.49952 ; E A = 0.00563

p 2 x = - 0.25321 x 2 + 1.12288 x - 0.56865 ; p 2 1.4 = 0.50709 ; E A = 0.00194

d p 1 x = 34.2858 x - 31.9248 ; p 1 1.4 = 16.0753 ; E A = 1.03065

p 2 x = 26.8531 x 2 - 42.2469 x + 21.7823 ; p 2 1.4 = 15.2688 ; E A = 0.22415

Exercício Resolvido #4

Lista 4 – Professor Mauro – UFRJ – Questão 3a adaptada

Sabendo-se que f 0.81 = 16.94410 , f 0.83 = 17.56492 , f 0.86 = 18.50515 e f 0.87 = 18.82091 , calcule um valor aproximado de f 0.84 , usando polinômio interpolador de Lagrange de grau n ≤ 1,2

Passo 1

Grau 1:

Para encontrar o polinômio de Lagrange de grau 1 vamos usar os pontos:

x 0 = 0.83

x 1 = 0.86

Temos então que:

p 1 x = y 0 L 0 + y 1 L 1 ,

onde:

y 0 = f 0.83 = 17.56492

y 1 = f 0.86 = 18.50515

L 0 = x - x 1 x 0 - x 1 = 0.86 - x 0.03 = 86 - 100 x 3

L 1 = x - x 0 x 1 - x 0 = x - 0.83 0.03 = 100 x - 83 3

Logo,

p 1 x = 31.341 x - 8.44811

Substituindo 0.84 no polinômio:

p 1 0.84 = 17.8783

Passo 2

Grau 2:

Para encontrar o polinômio de Lagrange de grau 2 vamos usar os pontos:

x 0 = 0.81

x 1 = 0.83

x 2 = 0.86

Temos então que:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2 ,

onde:

y 0 = f x 0 = 16.94410

y 1 = f x 1 = 17.56492

y 2 = f x 2 = 18.50515

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 0.83 x - 0.86 0.81 - 0.83 0.81 - 0.86 = 1000 x 2 - 1690 x + 713.8

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 0.81 x - 0.86 0.83 - 0.81 0.83 - 0.86 = - 1666.66 667 x 2 + 2783.3 333 3 x - 1161

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 0.81 x - 0.83 0.86 - 0.81 0.86 - 0.83 = 666.6 66 67 x 2 - 1093.3 333 3 x + 448.2

Logo,

p 2 x = 6 x 2 + 21.20 1 x - 4.16531

Substituindo 0.84 no polinômio:

p 2 0.84 = 17.8771

Passo 3

Grau 3:

Para encontrar o polinômio de Lagrange de grau 3 vamos usar os pontos:

x 0 = 0.81

x 1 = 0.83

x 2 = 0.86

x 3 = 0.87

Temos então que:

p 3 x = y 0 L 0 + y 1 L 1 + y 2 L 2 + y 3 L 3 ,

onde:

y 0 = f x 0 = 16.94410

y 1 = f x 1 = 17.56492

y 2 = f x 2 = 18.50515

y 3 = f x 3 = 18.82091

L 0 = x - x 1 x - x 2 x - x 3 x 0 - x 1 x 0 - x 2 x 0 - x 3 = x - 0.83 x - 0.86 x - 0.87 0.81 - 0.83 0.81 - 0.86 ( 0.81 - 0.87 ) = - x 3 + 2.56 x 2 - 2.1841 x + 0.6210 06 0.00006

L 1 = x - x 0 x - x 2 x - x 3 x 1 - x 0 x 1 - x 2 x 1 - x 3 = x - 0.81 x - 0.86 x - 0.87 0.83 - 0.81 0.83 - 0.86 0.83 - 0.87 = x 3 - 2.54 x 2 + 2.1495 x - 0.60604 2 0.000024

L 2 = x - x 0 x - x 1 x - x 3 x 2 - x 0 x 2 - x 1 x 2 - x 3 = x - 0.81 x - 0.83 x - 0.87 0.86 - 0.81 0.86 - 0.83 0.86 - 0.87 = - x 3 + 2.51 x 2 - 2.0991 x + 0.5849 01 0.000015

L 3 = x - x 0 x - x 1 x - x 2 x 3 - x 0 x 3 - x 1 x 3 - x 2 = x - 0.81 x - 0.83 x - 0.8 6 0.8 7 - 0.81 0.8 7 - 0.83 0.8 7 - 0.8 6 = x 3 - 2.5 x 2 + 2.0827 x - 0.5781 78 0.000024

Logo,

p 3 x = - 2.08333 x 3 + 11.2083 x 2 + 16.862 x - 2.96077

Substituindo 0.84 no polinômio:

p 3 0.84 = 17 . 8771

Resposta

p 1 0.84 = 17.8783

p 2 0.84 = 17.8771

p 3 0.84 = 17 . 8771

Exercício Resolvido #5

Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 258, exercício 10

Seja a tabela:

Usando um polinômio interpolador de grau 2 , trabalhe de dois modos diferentes para obter o valor estimado de x para o qual f x = 0.23 .

Passo 1

Então, os dois modos que vamos resolver essa questão são o seguinte. Primeiro, vamos encontrar uma função de interpolação para f x e igualar a 0.23 .

O segundo modo é meio não usual e normalmente não passaria pela cabeça da gente haha. Por que não interpolarmos x como função de y ao invés de y como função de x ? Nesse caso, bastaria substituirmos 0.23 na nossa função de interpolação! Maneiro né?

Passo 2

Vamos começar pelo primeiro modo! Como queremos um polinômio interpolador de grau 2 precisamos de três pontos. Vamos usar esses aqui:

x 0 = 0.25

x 1 = 0.30

x 2 = 0.35

Temos então que:

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2 ,

onde:

y 0 = f x 0 = 0.19

y 1 = f x 1 = 0.22

y 2 = f x 2 = 0.25

L 0 = x - x 1 x - x 2 x 0 - x 1 x 0 - x 2 = x - 0.30 x - 0.35 0.25 - 0.30 0.25 - 0.35 = 200 x 2 - 130 x + 21

L 1 = x - x 0 x - x 2 x 1 - x 0 x 1 - x 2 = x - 0.25 x - 0.35 0.30 - 0.25 0.30 - 0.35 = - 400 x 2 + 240 x - 35

L 2 = x - x 0 x - x 1 x 2 - x 0 x 2 - x 1 = x - 0.25 x - 0.30 0.35 - 0.25 0.35 - 0.30 = 200 x 2 - 110 x + 15

Logo,

p 2 x = 15 x + 1 25

Repare que aqui os x 2 se cancelaram! Por isso que ela não está do segundo grau haha. O próximo passo é igualarmos ela a 0.23 para acharmos o x :

15 x + 1 25 = 0.23

15 x + 1 = 5.75

x = 0.31667

Passo 3

Agora vamos reescrever essa tabela com x sendo função de y :

Agora vamos encontrar a função de interpolação de f y :

y 0 = 0.19

y 1 = 0.22

y 2 = 0.25

Temos então que:

p 2 y = x 0 L 0 + x 1 L 1 + x 2 L 2 ,

onde:

x 0 = f y 0 = 0.25

x 1 = f y 1 = 0.30

x 2 = f y 2 = 0.35

L 0 = y - y 1 y - y 2 y 0 - y 1 y 0 - y 2 = y - 0.22 y - 0.25 0.19 - 0.22 0.19 - 0.25 = 555.556 y 2 - 261.111 y + 30.5556

L 1 = y - y 0 y - y 2 y 1 - y 0 y 1 - y 2 = y - 0.19 y - 0.25 0.22 - 0.19 0.22 - 0.25 = - 1111.11 y 2 + 488.889 y - 52.7778

L 2 = y - y 0 y - y 1 y 2 - y 0 y 2 - y 1 = y - 0.19 y - 0.22 0.25 - 0.19 0.25 - 0.22 = 555.556 y 2 - 227.778 y + 23.2222

Logo,

p 2 y = 5 y - 0.2 3

Novamente os x 2 se cancelaram! E agora temos uma função de y ! Então podemos substituir direto o 0.2 3 e achar o x :

x = 0.31667

Resposta

x = 0.31667

Exercício Resolvido #6

Lista de Exercícios - FEI

Dada f x = ( x + 1 ) s e n ( 2 x + 3 ) . Pede-se:

a) Aproximar por um polinômio de Lagrange do 2º grau no intervalo [0,1];

b) Determinar o valor aproximado da raiz desta função no intervalo dado;

Passo 1

Fala galera, a primeira coisa a se fazer quando pedem pra gente o polinômio interpolador de lagrange é tabelar a função.

Nesse caso a questão diz que o intervalo [a,b] é nesse problema [0,1] e o polinômio é de 2º grau. Entãoooo, para termos um polinômio de segundo grau precisamos de 3 pontos tabelados né?

k = 3   pontos

n = k - 1 = 2 intervalos

Agora que a gente já sabe o número de pontos, bora calcular o passo h da tabela. A fórmula é: h = b - a n = 1 - 0 2 = 0.5

Isso quer dizer que os valores de x na nossa tabela crescem de 0.5 em 0.5. Ela é assim então:

Agora basta substituir os valores de x em f x = ( x + 1 ) s e n ( 2 x + 3 )

f 0 = 0 + 1 * s e n 2 * 0 + 3 = 0.1411

f 0.5 = 0.5 + 1 * s e n 2 * 0.5 + 3 = - 1.135

f 1 = 1 + 1 * s e n 2 * 1 + 3 = - 1.917

Prontinho, tá tabelado agora!!

Passo 2

Agora é a hora de aplicar a fórmula do polinômio de lagrange!!

P 2 x = f ( x 0 ) L 0 + f ( x 1 ) L 1 + f ( x 2 ) L 2

A gente pode tirar f ( x 0 ) ,     f ( x 1 ) ,     f ( x 2 ) diretinho da segunda linha da tabela. Agora bora montar os L s

L 0 = x - x 1 * ( x - x 2 ) x 0 - x 1 * ( x 0 - x 2 ) =   x - 0.5 * ( x - 1 ) 0 - 0.5 * ( 0 - 1 )

L 0 = 2 x 2 - 3 x + 1

L 1 = x - x 0 * ( x - x 2 ) x 1 - x 0 * ( x 1 - x 2 ) =   x - 0 * ( x - 1 ) 0.5 - 0 * ( 0.5 - 1 )

L 1 = - 4 x 2 + 4 x

L 2 = x - x 0 * ( x - x 1 ) x 2 - x 0 * ( x 2 - x 1 ) =   x - 0 * ( x - 0.5 ) 1 - 0 * ( 1 - 0.5 )

L 2 = 2 x 2 - x  

Passo 3

Botando tudo junto na fórmula do polinômio...

P 2 x = f ( x 0 ) L 0 + f ( x 1 ) L 1 + f ( x 2 ) L 2

P 2 x = 0.1411 * 2 x 2 - 3 x + 1 - 1.135 * - 4 x 2 + 4 x - 1.917 * 2 x 2 - x

Simplificando ficamos com...

P 2 x = 0.9882 x 2 - 3.0463 x + 0.1411

Show demais tá aí o polinômio de 2º grau que o professor pediu pra gente.

DICA: Mas como eu confiro se tá certinho meu polinômio?

Pega um valor de x da tabela e substituí no polinômio, se chega bem pertinho do valor da f ( x ) seu polinômio ta show de bolinhas!!

Passo 4

Bom agora ele quer saber a raíz né? Aí você deve estar pensando que esse polinômio é de 2º grau, então têm 2 raízes. É isso que o inimigo tinhoso quer que você pense!!

Se a gente olhar direitinho a tabela que a gente montou lá no passo 1, a f ( x ) só muda de sinal uma vez entre 0 e 0.5. Isso é sinal que tem uma raíz aí nesse intervalo!!

Com o polinômio que a gente criou só vale pro intervalo da tabela que é [0,1], então só podemos calcular qualquer raíz dentro do intervalo [0,1].

Então é só achar as raízes e descartar aquela que ta fora do intervalo [0,1]

0.9882 x 2 - 3.0463 x + 0.1411 = 0  

Δ = b 2 - 4 a c = - 3.0463 2 - 4 * 0.9882 * ( 0.1411 )

Δ = 8.7222

x = - b ± Δ 2 * a

x 1,2 = 3.0463 ± 8.7222 2 * 0.9882

x 1 = 3.0356 (FORA DO INTERVALO [0,1])

x 2 = 0.047 (Olha nossa raíz aííí)

Resposta

P 2 x = 0.9882 x 2 - 3.0463 x + 0.1411

x = 0.047

Exercício Resolvido #7

Lista de Exercícios - FEI

Um projétil é lançado a uma altura de 2 m do solo e sobe até 10 m de altitude, após 5 segundos. Depois de mais 3 segundos o projétil se encontra a 6 m do solo. Determinar quanto tempo levará para o projétil chegar ao chão, a partir do lançamento. Aplicar o polinômio de Lagrange.

Passo 1

Creeeedo maior cara de problema de física, saí fora!! Bom mas vamo lá. Nessa historinha que ele contou ele já deu a tabela que relaciona as alturas e o tempo pra gente né? Vamo ver aqui:

“é lançado a uma altura de 2 m do solo”

t = 0  

  y = 2

“sobe até 10 m de altitude, após 5 segundos”

t = 5  

  y = 10

“Depois de mais 3 segundos o projétil se encontra a 6 m do solo”

t = 5 + 3 = 8  

  y = 6

Então...

Passo 2

Agora é a hora de aplicar a fórmula do polinômio de lagrange!!

Como temos k = 3   pontos na tabela a ordem do polinômio será

n = k - 1 = 2

Então:

P 2 t = f ( t 0 ) L 0 + f ( t 1 ) L 1 + f ( t 2 ) L 2

A gente pode tirar f ( t 0 ) ,     f ( t 1 ) ,     f ( t 2 ) diretinho da segunda linha da tabela. Agora bora montar os L s

L 0 = t - t 1 * ( t - t 2 ) t 0 - t 1 * ( t 0 - t 2 ) =   t - 5 * ( t - 8 ) 0 - 5 * ( 0 - 8 )

L 0 = 0.025 t 2 - 0.325 t + 1

L 1 = t - t 0 * ( t - t 2 ) t 1 - t 0 * ( t 1 - t 2 ) =   t - 0 * ( t - 8 ) 5 - 0 * ( 5 - 8 )

L 1 = - 0.06667 t 2 + 0.5333 t

L 2 = t - t 0 * ( t - t 1 ) t 2 - t 0 * ( t 2 - t 1 ) =   t - 0 * ( t - 5 ) 8 - 0 * ( 8 - 5 )

L 2 = 0.0417 t 2 - 0.2083 t  

Passo 3

Botando tudo junto na fórmula do polinômio...

P 2 t = f ( t 0 ) L 0 + f ( t 1 ) L 1 + f ( t 2 ) L 2

P 2 t = 2 * 0.025 t 2 - 0.325 t + 1 + 10 * - 0.0667 t 2 + 0.5333 t + …

… + 6 * 0.0417 t 2 - 0.2083 t    

Simplificando ficamos com...

P 2 t = - 0.3668 t 2 + 3.433 t + 2

Show demais tá aí o polinômio de 2º grau.

Mas agora precisamos achar em quanto tempo o projétil chega ao chão.

Passo 4

Pra achar esse tempo, basta igualar o polinômio à zero.

P 2 t = - 0.3668 t 2 + 3.433 t + 2

Δ = b 2 - 4 a c = 3.433 2 - 4 * - 0.3668 * ( 2 )

Δ = 14.72

x = - b ± Δ 2 * a

x 1,2 = - 3.433 t ± 14.72 2 * ( - 0.3668 )

x 1 = - 0.5502   (Nada a ver esse tempo negativo)

x 2 = 9.91 (Olha nossa resposta aí)

Resposta

t = 9.91     s

Exercício Resolvido #8

Lista de Exercícios - FEI

Sabe-se que a equação 𝑥²−𝑙𝑛(𝑥)−2=0, admite uma raiz no intervalo [1,2], determine o valor desta raiz utilizando um polinômio interpolador de Lagrange sobre três pontos

Passo 1

Fala galera, a primeira coisa a se fazer quando pedem pra gente o polinômio interpolador de lagrange é tabelar a função.

Nesse caso a questão diz que o intervalo [a,b] é nesse problema [1,2]. E o professor fala de 3 pontos então...

k = 3   pontos

n = k - 1 = 2 intervalos

Logo teremos um polinômio de 2º grau

Agora que a gente já sabe o número de pontos, bora calcular o passo h da tabela. A fórmula é: h = b - a n = 2 - 1 2 = 0.5

Isso quer dizer que os valores de x na nossa tabela crescem de 0.5 em 0.5. Ela é assim então:

Agora basta substituir os valores de x em f x = x 2 - ln ⁡ x - 2

f 1 = 1 2 - ln ⁡ 1 - 2 =   - 1

f 1.5 = 1.5 2 - ln ⁡ 1.5 - 2 = - 0.155

f 2 = 2 2 - ln ⁡ 2 - 2 = 1.307

Prontinho, tá tabelado agora!!

Passo 2

Agora é a hora de aplicar a fórmula do polinômio de lagrange!!

P 2 x = f ( x 0 ) L 0 + f ( x 1 ) L 1 + f ( x 2 ) L 2

A gente pode tirar f ( x 0 ) ,     f ( x 1 ) ,     f ( x 2 ) diretinho da segunda linha da tabela. Agora bora montar os L s

L 0 = x - x 1 * ( x - x 2 ) x 0 - x 1 * ( x 0 - x 2 ) =   x - 1.5 * ( x - 2 ) 1 - 1.5 * ( 1 - 2 )

L 0 = 2 x 2 - 7 x + 6

L 1 = x - x 0 * ( x - x 2 ) x 1 - x 0 * ( x 1 - x 2 ) =   x - 1 * ( x - 2 ) 1.5 - 1 * ( 1.5 - 2 )

L 1 = - 4 x 2 + 12 x - 8

L 2 = x - x 0 * ( x - x 1 ) x 2 - x 0 * ( x 2 - x 1 ) =   x - 1 * ( x - 1.5 ) 2 - 1 * ( 2 - 1.5 )

L 2 = 2 x 2 - 5 x + 3  

Passo 3

Botando tudo junto na fórmula do polinômio...

P 2 x = f ( x 0 ) L 0 + f ( x 1 ) L 1 + f ( x 2 ) L 2

P 2 x = - 1 * 2 x 2 - 7 x + 6 - 0.155 * - 4 x 2 + 12 x - 8 + 1.307 * 2 x 2 - 5 x + 3  

Simplificando ficamos com...

P 2 x = 1.234 x 2 - 1.395 x - 0.839

Show demais tá aí o polinômio de 2º grau que o professor pediu pra gente.

DICA: Mas como eu confiro se tá certinho meu polinômio?

Pega um valor de x da tabela e substituí no polinômio, se chega bem pertinho do valor da f ( x ) seu polinômio ta show de bolinhas!!

Passo 4

Bom agora ele quer saber a raíz né? Aí você deve estar pensando que esse polinômio é de 2º grau, então têm 2 raízes. É aí que tá aquela pegadinha

Se a gente olhar direitinho a tabela que a gente montou lá no passo 1, a f ( x ) só muda de sinal uma vez entre 1.5 e 2. Isso é sinal que tem uma raíz aí nesse intervalo!!

Com o polinômio que a gente criou só vale pro intervalo da tabela que é [1,2], então só podemos calcular qualquer raíz dentro do intervalo [1,2].

Então é só achar as raízes e descartar aquela que ta fora do intervalo [1,2]

1.234 x 2 - 1.395 x - 0.839 = 0  

Δ = b 2 - 4 a c = - 1.395 2 - 4 * 1.234 * ( - 0.839 )

Δ = 6.087

x = - b ± Δ 2 * a

x 1,2 = 1.395 ± 6.087 2 * 1.234

x 1 = 1.565 (Nossa Raíz)

x 2 = - 0.434 (FORA DO INTERVALO)

Resposta

x = 1.565

Exercícios de Livros Relacionados

13. Sendo p n x = ∑ k = 0 n L k x f ( x k ) o polinômio que interpola f ( x ) em x 0 , x 1 , … . , x n na forma de Lagrange mostre que... ∑ k = 0 n L k ( x ) = 1 ,∀ x (Sugestão: Interpole a função f x
A integral elíptica completa é definida por: K k = ∫ 0 π 2 d x 1 - k 2 sin 2 ⁡ x 1 2 Por uma tabela de valores dessa integral encontramos:K 1 =1.5708 ;K 2 = 1.5719 ;K 3 = 1.5739 Determinar K ( 2.5 ) ,
Construir os polinômios de interpolação, na forma de Lagrange, para a função y = sin ⁡ π x , escolhendo os pontos: x 0 = 0;x 1 = 1 6;x 2 = 1 2.
Dar uma outra prova de unicidade do polinômio de interpolação P n ( f ; x ) de uma função y= f ( x ) sobre o conjunto de pontos x 0 , x 1 , .. ., x n . D n ( x ) = P n ( f ; x ) - Q n ( f ; x ) .
Conhecendo-se a tabela:calcular um limitante superior para o erro de truncamento quando calculamos cos ⁡ 1,05 usando polinômio de interpolação sobre 4 pontos.