Resolva o exercício proposto na introdução deste capítulo. Verifique que um polinômio de grau 2 é uma boa escolha para obter f(32.5); use um processo de interpolação linear para obter o ponto x para o qual f(x) = 0.99837.
Passo 1
Eai pessoal, essa é tranquila, vamo que vamo...
Passo 2
Primeiro, vamos ver a tabela dos valores que temos:
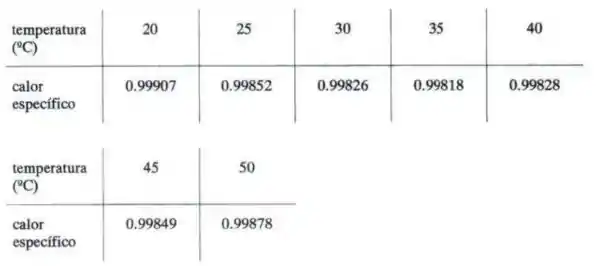
Passo 3
Nesse caso, usaremos o polinômio de grau 2 aqui, pra resolver a primeira parte, tomaremos o calor específico como e a temperatura como
Tomando
Agora, resolvendo o sistema:

Na ordem,
Chegamos então, à:
Substituindo, temos:
Passo 4
Agora, vamos aproveitar esse polinômio que já calculamos para achar tal que :
Resolvendo isso, acharemos:
Hmmm, como queremos que , olhando para a tabela, vemos que deve estar entre e , logo, vamos usar, beleza?
Só isso! Acabou 😊.