Eliminação De Gauss
Produzido por Bruno PestanaTeoria
Fala aí! Hoje vamos aprender um pouquinho sobre o método de eliminação de Gauss e também como montar um algoritmo pra resolver esse negócio aí.
Talvez você já conheça esse processo pelo nome de escalonamento! Mas independente do nome, veremos como a eliminação de Gauss fornece um método para a resolução de sistemas lineares a partir de um sistema linear triangular equivalente.
Calma, já te explico tudo isso aí! Vem comigo 😆
Só não deixa de conferir também 👇😁
- Introdução a sistemas lineares e não lineares.
- Pivoteamento.
- Método iterativo de Gauss-Jacobi.
- Quer aprender a programar?
Método de Gauss
O método de Gauss consiste em transformar um sistema linear
Não tenho a menor ideia do que isso significa.
Vem cá que eu te mostro! Considere esse sistema linear aqui:
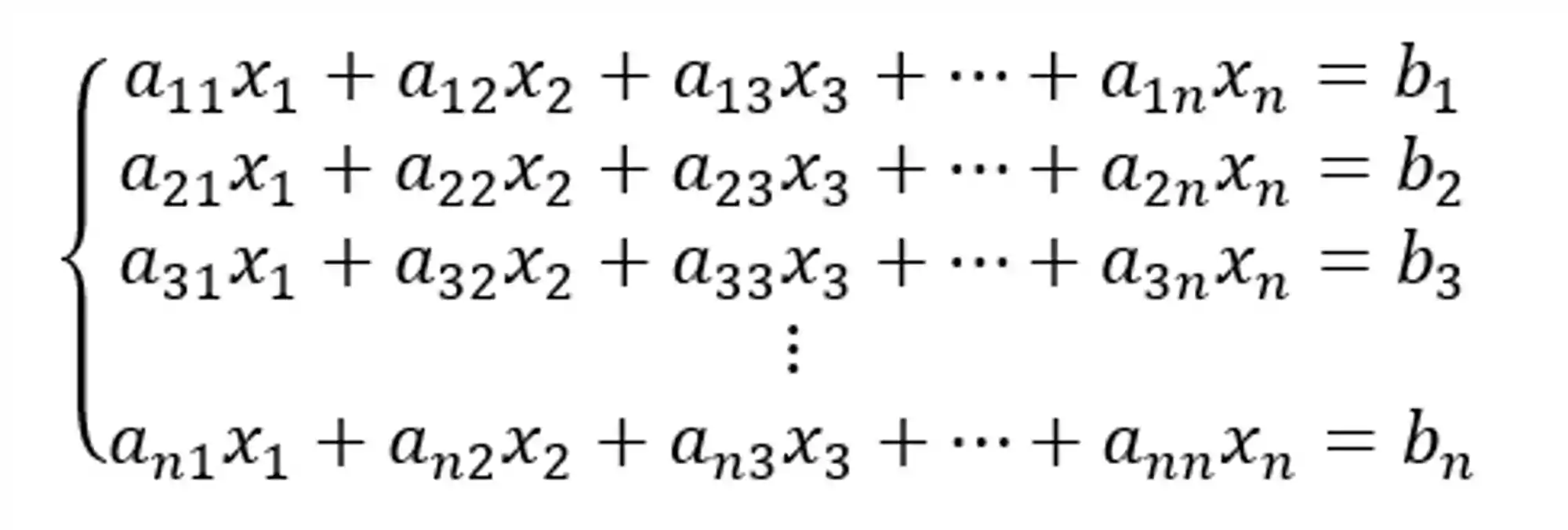
A gente pode representar ele na forma de matriz estendida, pra ficar mais fácil de trabalhar.
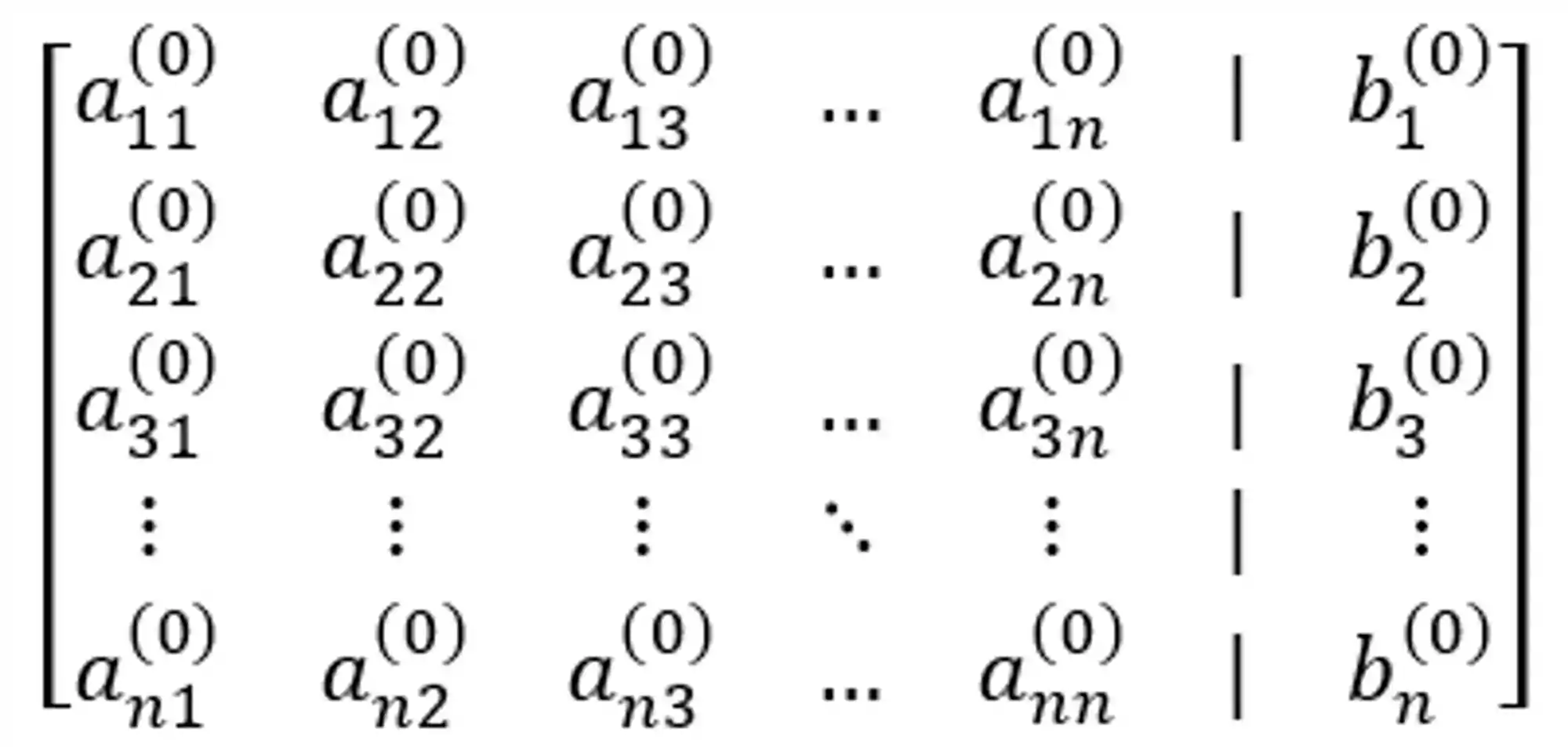
Só pra deixar claro:
Beleza, no fim do processo de eliminação de Gauss, vamos ficar com um sistema dessa forma aqui:
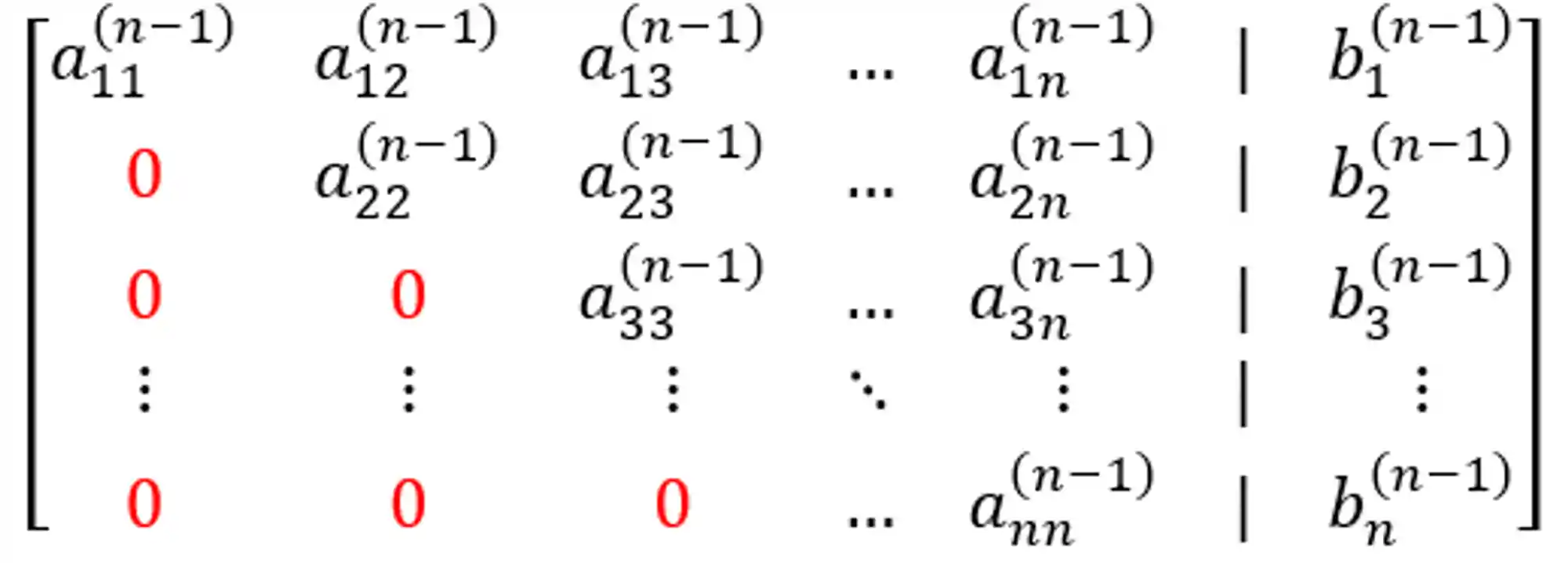
Reparou como todos os valores abaixo da diagonal principal valem zero? Isso que quer dizer sistema ou matriz triangular superior, porque os zeros formam um triângulozinho ali abaixo da diagonal e os valores não nulos ficam no triângulo acima da diagonal.

Aí, a solução desse sistema obtido vai ser solução do sistema original! E a resolução desse aí é muuuuito mais fácil.
Então bora ver como que faz esse negócio?
Como resolver sistemas lineares usando o método de Gauss?
Como a gente vai transformar esses números abaixo da diagonal em zeros?
É o seguinte: para eliminar a incógnita
Esse
Mas falando desse jeito aí parece ser mais difícil do que realmente é. É melhor vermos como fica esse negócio na prática mesmo.
Se liga nesse vídeo maravilhoso preparado aqui pra você, ou então segue comigo na resolução do exercício logo abaixo 👇
Exemplo: Resolva o sistema abaixo pelo método de Gauss.
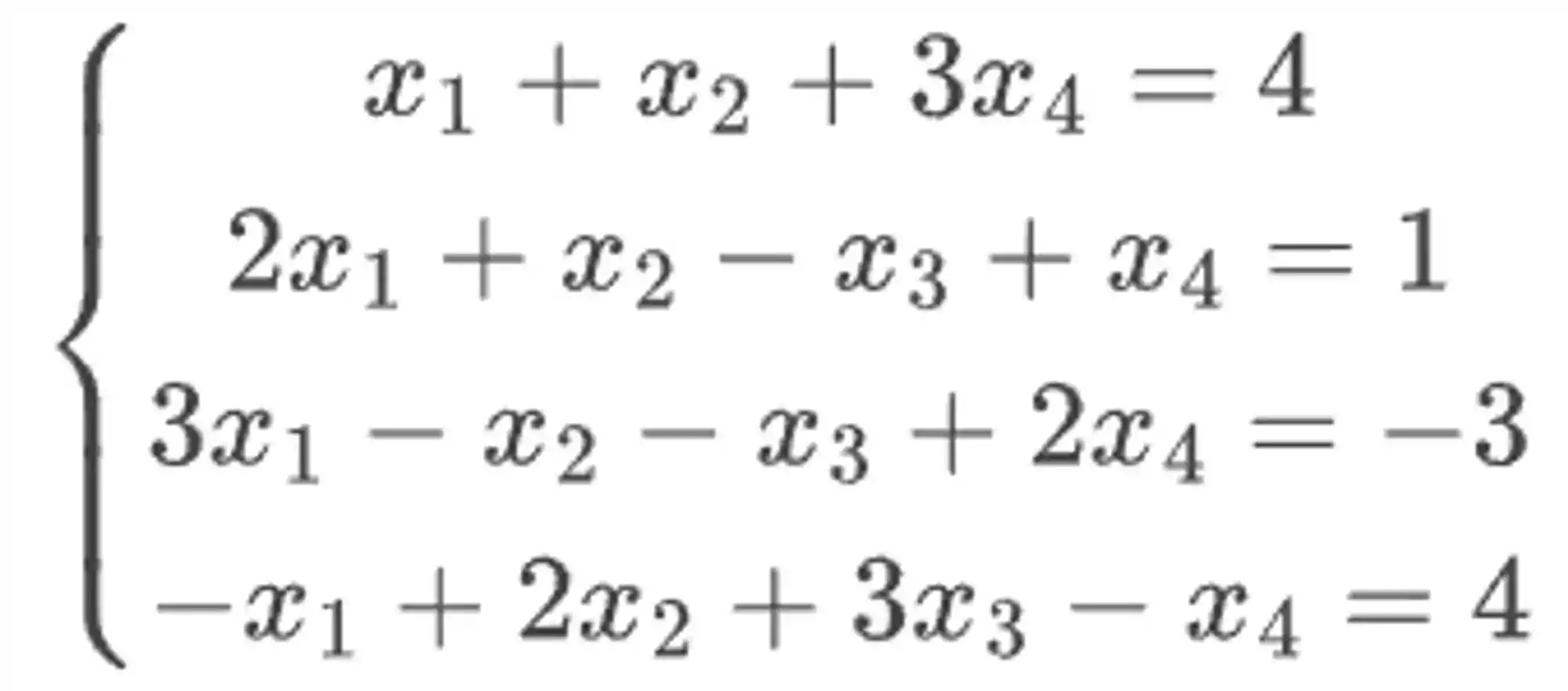
Passo 1: Colocar na forma de matriz estendida.
É só copiar os coeficientes de um lado e os resultados do outro lado dessa barrinha vertical dentro da matriz.

Tomando cuidado com os sinais e com os coeficientes nulos, viu?!
Passo 2: Zerar tudo abaixo do pivô da primeira linha.
O primeiro pivô é aquele
Para isso, vamos fazer:
Os multiplicadores dessa etapa vão ser:
Então:
Então é só fazer a linha 2 menos duas vezes a linha 1!

Para zerarmos o 3, fazemos a linha 3 menos três vezes a linha 1.

Por fim, fazemos a quarta linha mais a primeira pra zerar aquele
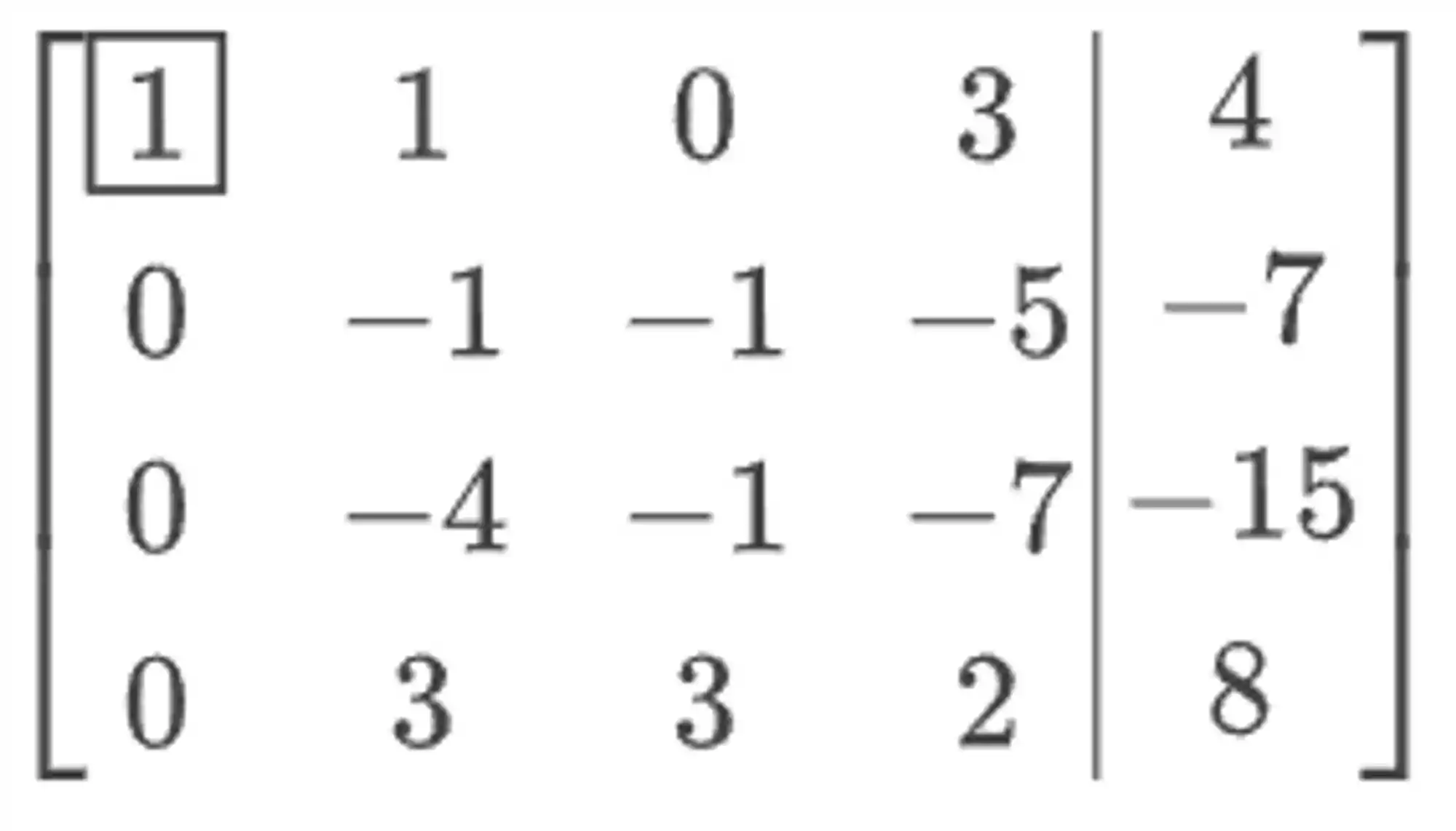
Passo 3: Zerar tudo abaixo do pivô da segunda linha.
O pivô da segunda linha agora é o
Os multiplicadores aqui vão ser:
Então, para zerar aquele
É só fazer a terceira linha menos quatro vezes a segunda.

Para zerarmos o
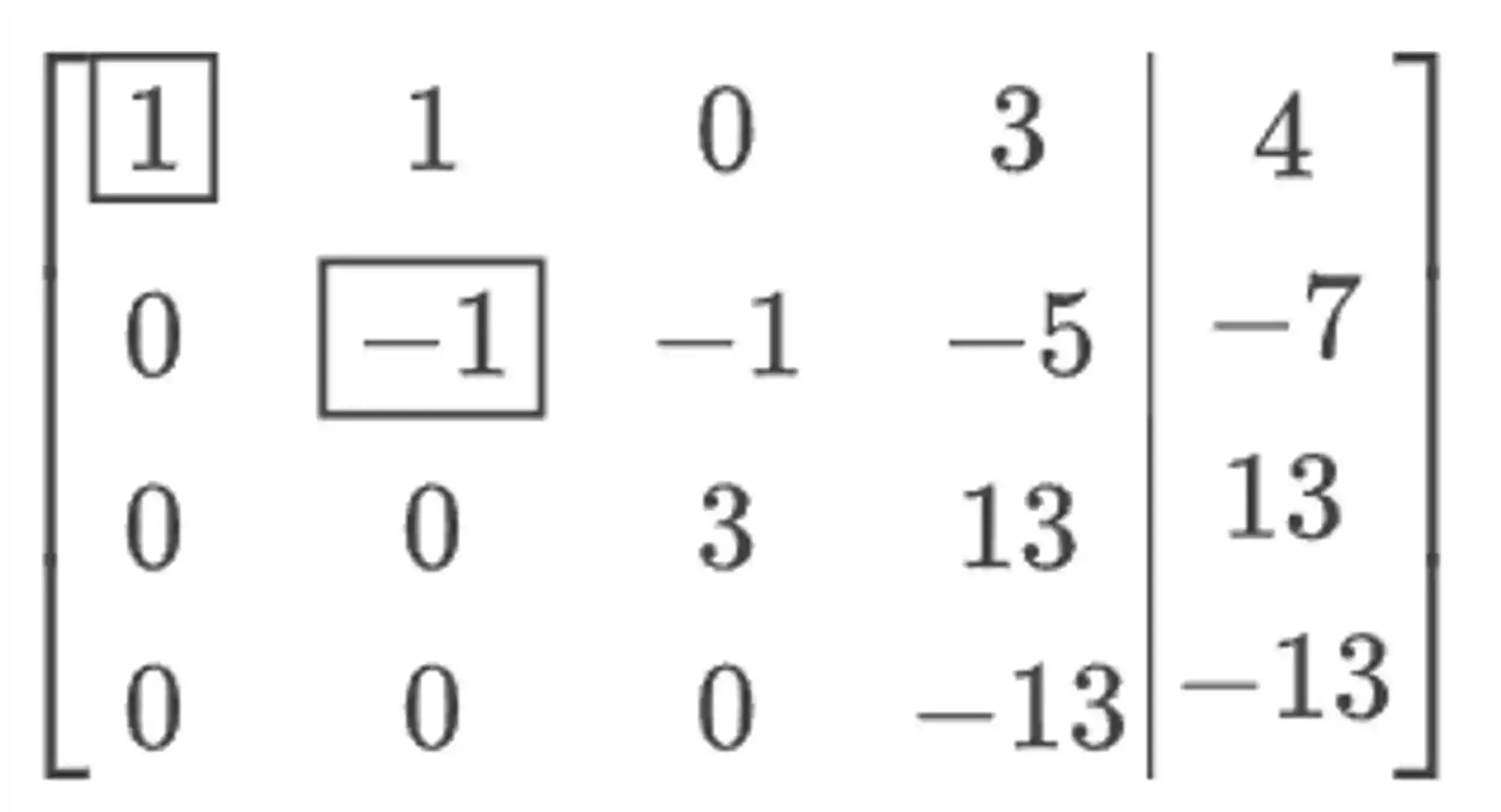
Opaa, já vi apareceu nossa matriz triangular ali! Então já podemos seguir em frente para a próxima fase, que é a da resolução.
Passo 5: Voltar para a forma de sistema e resolver por retrossubstituição.
Reescrevendo aquela matriz obtida na forma de sistema, temos o seguinte:
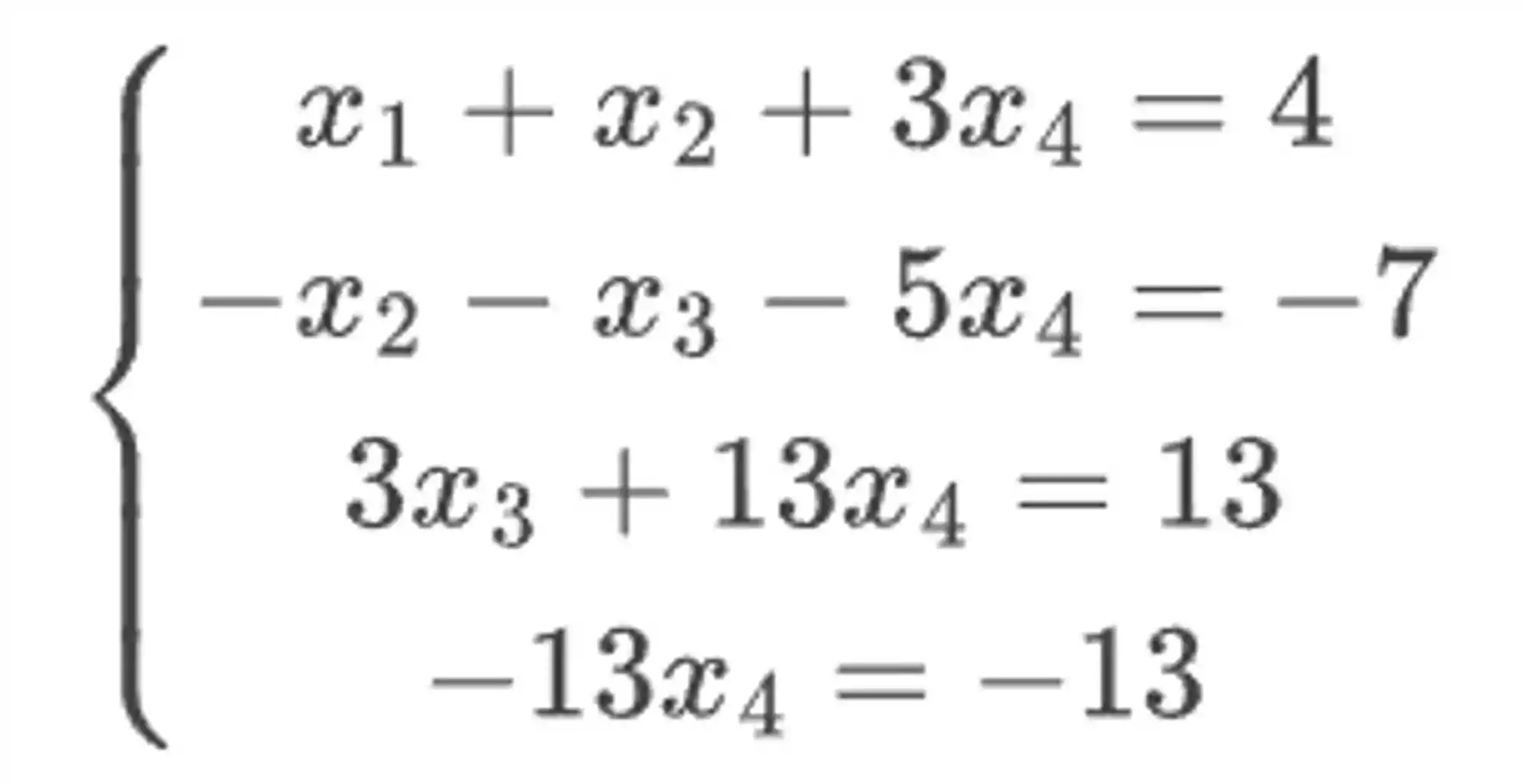
Olha que beleza: aquela última equação só tem uma incógnita 😋
Essa que é a vantagem de usar o método de Gauss, sempre teremos uma das equações com somente uma incógnita. E aí é só ir resolvendo de baixo para cima.
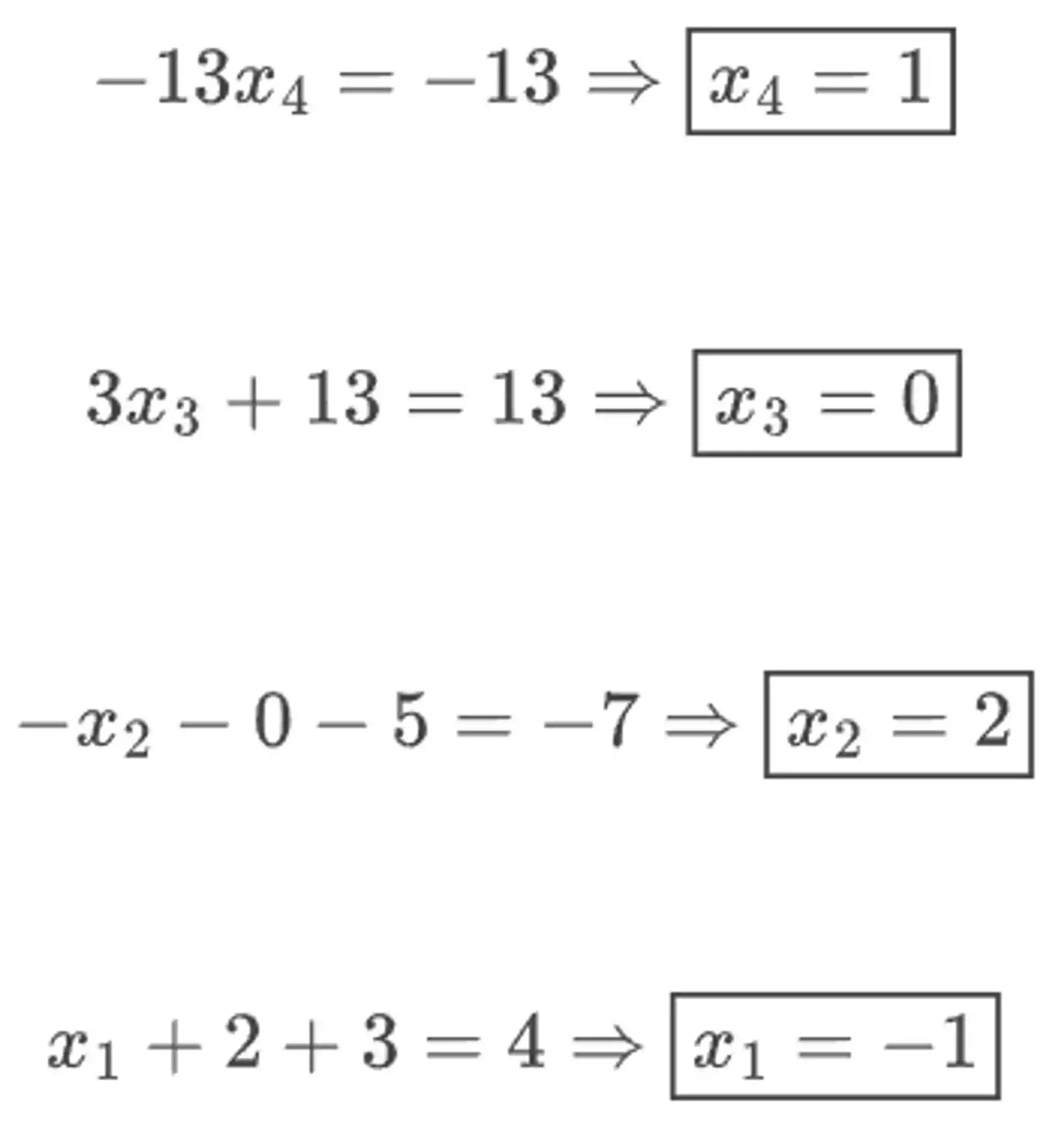
Algoritmo do Método de Eliminação de Gauss
A grande vantagem do Cálculo Numérico é que podemos escrever algoritmos e soltar tudo isso no cérebro dos nossos computadores pra eles se virarem, não é? Então bora ver como fica o algoritmo desse método aqui!
Algoritmo da Fase 1: Eliminação
Passo 1: Dados iniciais.
Os dados que o seu programa vai receber de você são:
- Matriz quadrada
. - Vetor solução
.
Passo 2: Percorrer as linhas de
Passo 3: Escolher pivô da
Passo 4: Para cada ‘
Passo 5: Definir o multiplicador
Passo 6: Para cada ‘
Passo 7: Para cada
Passo 8:
Terminados todos os
Algoritmo da Fase 2: Retrossubstituição
Passo 1: Dados iniciais.
Os dados que o seu programa vai receber de você são:
- Matriz quadrada triangular
(passada do algoritmo anterior). - Vetor solução
(também recebido do anterior).
Passo 2:
Passo 3:
Passo 4:
Passo 5:
Passo 6:
Passo 7:
Passo 8:
Passo 9: Enquanto
Passo 10:
Passo 11:
Passo 12: Enquanto
E fechamos nosso exercício, bora praticar mais um poquinho?
Como resolver sistemas lineares usando o método de Gauss?
Exemplo: Resolva o sistema abaixo pelo método de Gauss.
Algoritmo do Método de Eliminação de Gauss
Exercícios Resolvidos
Exercício Resolvido #1
UFRGS-REAMAT- Cálculo Numérico- livro Scilab-Adaptada.
Resolva o sistema linear abaixo utilizando o método da Eliminação de Gauss:
Foi necessário trocar alguma linha?
Passo 1
Com esse sistema linear, conseguimos construir essas matrizes:
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
:
Opa, para facilitar nossa vida, podemos trocar a segunda e a terceira linhas:
:
Continuando:
:
Como vemos, foi necessário trocar uma linha (a segunda com a terceira linha)
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
Da terceira equação:
Substituindo na segunda equação:
Substituindo e na primeira equação:
Logo, ficamos com:
Resposta
Exercício Resolvido #2
Elaboração Própria.
Utilizando o método da Eliminação de Gauss, verifique se é possível resolver o sistema linear abaixo:
Passo 1
Vamos utilizar o método da Eliminação de Gauss para tentar encontrar a solução do problema. O primeiro passo é representar esse sistema em forma de matriz:
Com esse sistema linear, conseguimos construir essas matrizes:
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
:
:
Agora vamos para o segundo pivô:
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
Como temos 3 incógnitas e apenas 2 equações, nosso sistema tem infinitas soluções!!
Como poderíamos achar uma resposta pra esse problema, então? Vamos deixar tudo em função de uma das variáveis:
E
Como :
Logo, dizemos que , e é qualquer número pertencente aos reais.
Então, foi possível resolver o sistema!
Resposta
Sim, foi possível e:
Exercício Resolvido #3
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 181, exercício 5.
Resolva o sistema linear abaixo utilizando o método da Eliminação de Gauss:
Passo 1
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
:
:
:
:
:
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
De :
De :
De :
Logo, ficamos com:
Resposta
Exercício Resolvido #4
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 368, exercício 4.
Use a eliminação gaussiana com Retrosubstituição e aritmética de ponto flutuante de dois dígitos com arredondamento para resolver os sistemas abaixo. Não reorganize as equações. (A solução exata dos sistemas é , , )
Passo 1
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
:
:
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Passo 4
Passando para a forma de matriz aumentada:
Passo 5
Fase 1 – Eliminação:
:
:
:
Passo 6
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Resposta
Exercício Resolvido #5
Lista 4 – Professora Susana – exercício 3.
Tente resolver o seguinte sistema pela eliminação de Gauss. O que acontece? O que pode concluir?
Passo 1
A matriz aumentada fica:
Passo 2
Fase 1 – Eliminação:
:
:
:
Passo 3
Fase 2 – Retrosubstituição:
Eita. E agora? Não dá pra aplicar a retrosubstituição já que a última linha sumiu. Repare que só sobraram equações para variáveis! Ou seja, alguma variável está livre. Isso quer dizer que temos infinitas soluções! Vale ressaltar que um algoritmo de computador não conseguiria resolver isso pois envolveria dividir .
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 369, exercício 5.
Use o algoritmo da eliminação de Gauss para resolver os sistemas abaixo, se possível, e determine se alguma troca de linhas é necessária.
Passo 1
Passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
:
:
Repare que agora temos um pivô zero, então nosso algoritmo ia para o espaço! Se fosse uma máquina teria acusado erro aqui e esse é um problema muito sério desse método. Mas como não somos máquinas vamos trocar as linhas e continuar:
:
Passo 3
Fase 2 – Retrosubstituição:
Voltando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
E fizemos troca de linhas.
Passo 4
Passando para a forma de matriz aumentada:
Passo 5
Fase 1 – Eliminação:
:
:
:
Passo 6
Fase 2 – Retrosubstituição:
Voltando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
E não fizemos nenhuma troca de linhas.
Passo 7
Passando para a forma de matriz aumentada:
Passo 8
Fase 1 – Eliminação:
:
:
:
:
:
Passo 9
Fase 2 – Retrosubstituição:
Voltando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
E não fizemos nenhuma troca de linhas.
Passo 10
Passando para a forma de matriz aumentada:
Passo 11
Fase 1 – Eliminação:
:
:
:
:
:
:
Passo 12
Deu pra ver que o sistema não tem solução? Se liga na última equação! Ela diz que , o que é obviamente impossível!
Resposta
. Fizemos uma troca de linhas.
. Não fizemos troca de linhas.
. Não fizemos troca de linhas.
Sistema impossível.
Exercício Resolvido #7
Lista 3 – Professor Daniel – UFRJ – Questão 2
Resolva os sistemas lineares abaixo utilizando o método de eliminação de Gauss, fazendo arredondamento com casas decimais:
Solução exata:
Solução exata:
Passo 1
Passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
:
:
Passo 3
Fase 2 – Retrosubstituição:
Voltando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Passo 4
Passando para a forma de matriz aumentada:
Passo 5
Fase 1 – Eliminação:
:
:
:
Passo 6
Fase 2 – Retrosubstituição:
Voltando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Um resultado bem distante do real né? Pra você ver a diferença que algumas casas decimais fazem!
Resposta