Exercícios de Método da Eliminação de Gauss - Lista de Exercícios Resolvida

Use o algoritmo da eliminação de Gauss para resolver os sistemas abaixo, se possível, e determine se alguma troca de linhas é necessária.

Resolva os sistemas lineares abaixo utilizando o método de eliminação de Gauss, fazendo arredondamento com casas decimais:

Solução exata:

Solução exata:

Use a eliminação gaussiana com Retrosubstituição e aritmética de ponto flutuante de dois dígitos com arredondamento para resolver os sistemas abaixo. Não reorganize as equações. (A solução exata dos sistemas é , , )

Resolva o sistema linear abaixo utilizando o método da Eliminação de Gauss:

Resolva o sistema linear abaixo utilizando o método da Eliminação de Gauss:

Foi necessário trocar alguma linha?

Utilizando o método da Eliminação de Gauss, verifique se é possível resolver o sistema linear abaixo:

Tente resolver o seguinte sistema pela eliminação de Gauss. O que acontece? O que pode concluir?

2. Considerando os pontos da tabela abaixo:

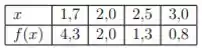
a) Ajuste a função aos pontos dados. Obs.: O sistema linear resultante deve ser resolvido pelo método de eliminação de Gauss.

b) Calcule o valor de a partir do modelo encontrado.

c) Baseado no erro quadrado, indique se o modelo encontrado em (a) é mais preciso do que a opção linear .