Esboço de Gráfico – Assíntota Oblíqua
Produzido por Arthur Melo de AlmeidaTeoria
Introdução
Ok, ok. Agora vamos falar de alguns problemas de esboço de gráfico que contém assíntota oblíqua e, principalmente, como devemos desenhá-la para não dar bobeira, mas relaxe, o pior e mais volumoso do esboço de gráfico você já viu como faz.
Assíntota obliqua
A assíntota obliqua, caso você não se lembre, ocorre quando a função se aproxima muito de uma reta qualquer quando a variável da função vai para infinito:
Onde e são as constantes dessa reta.
Como a função tá se aproximando cada vez mais de uma reta, então é natural que a diferença entre as duas caia para zero, então:
Onde:
Se os dois limites existirem, temos uma assíntota oblíqua. Ficou com alguma dúvida? Temos um tipo bem legal que fala só dessa assíntota, procura lá!
Como esboçar uma
A assíntota oblíqua terá a seguinte forma:
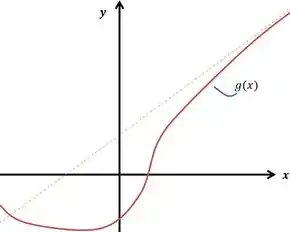
Onde a reta pontilhada é reta para qual a função se aproxima. Quando você for calcular os limites:
Você encontrará também os coeficientes dessa reta pontilhada. Uma vez com ele, marque, no gráfico, dois pontos que pertencem à reta, como a interseção com os eixos e e traceje a reta ligando esses pontos.
Daí é só desenhar a função se aproximando dessa reta na hora do esboço ;-).