Esboço De Gráfico
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí! Seja muito bem vindo ao Responde Aí! Bora conversar sobre Esboço de Gráfico?
Já vamos começar com tudo! Eu quero que você me diga como você faria o esboço do gráfico da seguinte função:
Difícil, não é?! 😱
Existem algumas funções clássicas, tipo a de segundo grau que a gente aprende a esboçar lá no ensino médio. Mas como fazer um esboço de um gráfico quando temos uma função mais complexa?
A gente vai aprender hoje, mas já vou te dando um spoiler, essa técnica de esboço de gráfico é uma aplicação de derivadas!
Vamos ver como fazer um esboço de um gráfico?! Se liga nesse vídeo então 👇
Ou continua comigo no textinho e vamos ver como esboçar o gráfico da função acima, passo a passo! 🤩
1º Passo: Domínio
Nosso primeiro passo é a análise do domínio para nossa função!
O domínio de uma função é o conjunto de valores que o seu
Basicamente você tem que olhar pra função e se perguntar “o que o x pode ser pra não dar ruim?”
A resposta é o domínio da função! Para isso:
- Os denominadores devem ser
; - Sempre que houver raiz de índice par temos que forçar o que está dentro dela a ser
; - Para funções logarítmicas tipo
temos que ter .
Podemos escrever então o domínio:
2º Passo: Assíntotas Verticais e Horizontais
Outra parte importante são as assíntotas!
Temos que pegar a função que estamos trabalhando e fazer o cálculo de assíntotas horizontais e verticais!
Você pode clicar aqui para ver como calcular assíntotas horizontais e verticais!
Para nosso exemplo temos assíntotas verticais em:
3º Passo: Derivada Primeira
Show! Agora vamos derivar nossa função para achar os pontos críticos:
Para isso vamos usar a regra do quociente:
Resolvendo, temos:
- Clique para saber mais:
4º Passo: Pontos críticos, Crescimento e Decrescimento
Os pontos críticos acontecem quando
Logo os pontos críticos são
Substituindo os pontos onde
Logo,
5º Passo: Derivada Segunda
Derivando a função novamente, para encontrar os pontos de inflexão:
6º Passo: Pontos de Inflexão e Análise do Sinal para concavidade
Os pontos de inflexão acontecem quando a derivada segunda é igual a zero ou temos uma indeterminação, para isso devemos ter:
Logo, nossos pontos de inflexão são:
7º Passo: Esboço
Enfim, podemos então começar a desenhar? Então arranja um bom pedaço de papel e vamos lá!
Show, a primeira coisa que faremos é marcar as assíntotas com uma linha fraca:
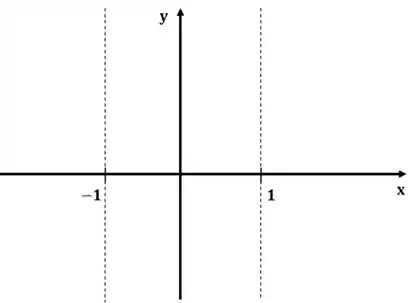
Beleza. Agora marcaremos os pontos críticos:
Marcaremos as regiões de crescimento e decrescimento com retas, também fracas, assim:
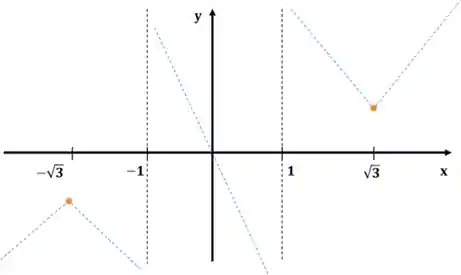
A reta simplesmente serve pra ilustrar o comportamento da função. Quando a função é crescente, desenhamos uma reta crescente, e quando é decrescente, uma reta decrescente.
Agora, marcamos os pontos de inflexão. Mesmo esquema dos pontos críticos. Eu gosto de marcar eles em cima das retas que já estão desenhadas, mas você pode fazer como quiser.
E marcamos as concavidades de acordo com os intervalos e também de acordo com a nossa técnica.
Quando a concavidade é pra baixo, a curva passa por cima da reta. Quando é pra cima, a curva passa por baixo. Com relação às assíntotas você só tem que lembrar que a função não encosta nelas. Ela vai se aproximando à medida que vamos ao infinito!
Nossa versão final do esboço do gráfico fica assim:
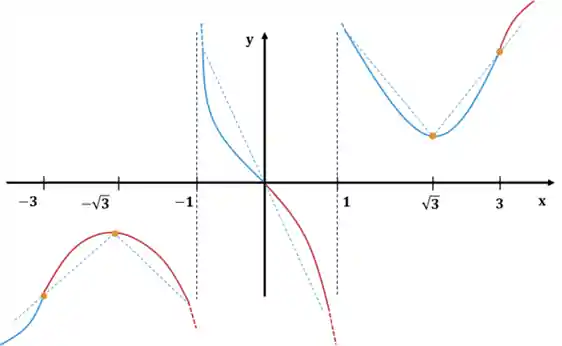
Agora vamos praticar com exercícios?!