Problemas De Otimização
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí! Hoje vamos aprender sobre problemas de otimização e como resolvê-los!
A ideia de uma otimização é encontrar a melhor solução para um problema matemático, e isso será feito por meio dos valores máximos e mínimos de uma função! Bora ver isso aí mais explicadinho com um exercício resolvido passo a passo?
⭐ Veja também ⭐
O que são problemas de otimização?
Um problema de otimização é aquele que descreve uma situação que pode ser descrita por uma função matemática e cuja solução envolve a determinação dos valores extremos dessa função.

Tendi foi nada.
Faz o seguinte, vamos imaginar a seguinte situação: o dono de um mercadinho percebe que está comprando mais bananas do que consegue vender, então, ele quer descobrir quantas bananas deve passar a comprar para ter um custo mínimo, mas continuar ganhando dinheiro.
Para ajudar esse rapaz aí, a gente tem que fazer uma otimização! Assim, conseguiremos achar qual o custo mínimo possível para o dono do mercado continuar ganhando dinheiro.
Mas uma otimização de quê? 🤔
Lembra que eu falei que a situação tem que ser descrita por uma função matemática? Então, vai ser essa função que queremos otimizar, para obter seus valores de máximo ou de mínimo.
Apesar disso aí parecer aqueles exemplos que a gente só vê na prova de matemática, problemas desse tipo são muito comuns na vida real!
A gente se depara com um problema de otimização, por exemplo, quando vai determinar o ponto da órbita de um cometa mais próximo da terra, a velocidade mínima de um foguete para que consiga escapar da atmosfera terrestre, a quantidade mínima de material usado para embalar algum produto, e outras inúmeras situações.
Bora ver o que a gente pode fazer para ajudar o dono do mercadinho?
Como resolver problemas de otimização?
Vamos ver o passo a passo para resolver problemas de otimização de uma forma geral e já aplicar isso aí no problema descrito anteriormente.
Passo 1
O primeiro passo para resolver esse tipo de problema é encontrar a função matemática que o descreve.
Em alguns exercícios, você vai ter que interpretar a situação e descobrir qual é essa função por conta própria. Mas relaxa que os casos mais clássicos sempre seguem a mesma receitinha.
Em outros casos, essa função vai ser dada de graça. Nosso problema do mercadinho é desse segundo tipo.
Vamos supor que a função que relaciona o custo
Passo 2
Com a função em mãos, devemos encontrar seus pontos críticos.
Como fazemos isso?
Primeira derivada igual a zero!
Vamos derivar a função anterior em relação à variável
E fazendo isso aí igual a zero:
Como
Passo 3
Beleza, temos então o valor para um ponto crítico dessa função, mas a gente precisa saber se esse ponto é de máximo ou de mínimo. Senão, a gente pode acabar levando o coitado do dono do mercado à falência!
E como fazemos isso aí? Pelo teste da primeira derivada!
É só olhar o sinal da derivada à esquerda do ponto crítico encontrado e à direita também. Saca só esse resuminho:

Vamos pegar o ponto
Como a derivada é negativa à esquerda e positiva à direita do ponto
Passo 4
Esse passo aqui é só pra você ficar atento ao seguinte: será que o ponto que encontramos é máximo ou mínimo local ou global?
Para termos certeza, temos que avaliar se o valor obtido quando substituímos
O custo para o ponto mínimo encontrado é:
E esse valor tem que ser comparado com as fronteiras, para ver se ele é de fato o menor possível para a função.
Para esse problema aqui, as fronteiras ocorrem com
Vamos testar essas fronteiras por meio de limites:
Então o ponto encontrado realmente é mínimo global da função. Nosso problema tá resolvido!
Como resolver problemas de otimização?
Exercícios Resolvidos
Exercício Resolvido #1
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 276-73.
A altura de um corpo que se desloca verticalmente é dada por:
Com em metros e em segundos. Determine a altura máxima do corpo.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
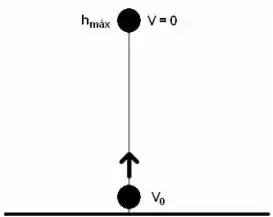
Passo 2
Analisando a equação e o esquema, chegamos na função que desejamos otimizar em função de apenas uma variável.
Note, que (velocidade inicial), (aceleração da gravidade) e (posição inicial) são valores constantes. Deste modo, o tempo é a única variável.
Para encontrar o máximo da função , vamos derivar essa função.
Passo 3
Agora, para achar o ponto de máximo, temos que encontrar os pontos críticos. Para isso, derivamos:
Os pontos críticos ocorrem onde a derivada não existe ou é zero. Como se trata de um polinômio, ela vai sempre existir. Vamos ver quando será zero:
Passo 4
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Uma forma de determinar a presença de máximos e mínimos e pelo teste da segunda derivada. Então vamos aplicá-lo:
Como a questão garante que . A segunda derivada é negativa no ponto crítico, ou seja, temos um ponto de máximo.
Passo 5
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não há outros pontos críticos na função, então não precisamos comparar com outros pontos.
Passo 6
Vamos verificar agora as fronteiras (menor e maior tempos) para garantir que este é um máximo global (altura máxima).
A função começa em (menor tempo), uma vez que o tempo não pode ser negativo. Para tal valor:
Para o maior tempo, vamos considerar , então vamos aplicar o limite:
No Passo 3, encontramos o ponto crítico:
Comparando os valores de menor e maior tempo com o ponto crítico, vemos que é máximo global.
Assim, o para esse tempo será:
Resposta
Exercício Resolvido #2
UFF - Cálculo IA – GMA – 2008.2 – Lista 16 - 10
Um fabricante produz por semana toneladas de um certo produto. O preço de venda é de unidades monetárias por tonelada do produto e está relacionado com por , . O custo de produção é de unidades monetárias. Determine para que o lucro seja máximo. Determine, também, o lucro máximo.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Não tem muito o que desenhar aqui, então vamos para o passo 2.
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Tá, vamos ver todas as informações que o problema nos deu aqui.
é a quantidade de produtos. é o preço de venda. Temos também:
Que é o custo de produção. Não é, porém, essa função que ele quer otimizar. É a função lucro que será a venda menos o custo:
Onde é o preço de cada unidade multiplicado pela quantidade delas.
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
O problema é que não é constante. Depende de . Temos que deixar isso aí em função de para podermos otimizar. Então voltamos na primeira equação e isolamos :
O que, se substituirmos os valores das relações do enunciado, fica assim:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Para acharmos os pontos críticos, onde estarão localizados os pontos de máximo e mínimo, devemos derivar:
Os pontos críticos estão onde a derivada não existe ou é zero. Ela sempre vai existir, pois é um polinômio. Vamos ver quando é zero:
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Podemos escolher um valor à esquerda e outro à direita :
Como é positiva à esquerda e negativa à direita, temos aí um ponto de máximo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não há outros máximo para comparar, então vamos para o outro passo.
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
pode ir de zero, pois não tem como ter quantidade negativa, até mais infinito.
E:
No nosso ponto de máximo:
Comparando com outros valores, concluímos que se trata de um ponto de máximo global.