Taxa Relacionada – Casos Clássicos
Produzido por Arthur Melo de AlmeidaTeoria
Pitágoras
Quase sempre a equação que relaciona as variáveis do problema não é fornecida no enunciado. Aí que mora grande parte da dificuldade de taxas relacionadas.
Um problema clássico aqui: Imagine que José, o desatento, tinha uma escada de de comprimento e a apoiou em uma parede. Como não se preocupou em deixá-la firme, a escada, agora, está escorregando de forma que sua base aumenta : O quanto variará a altura quando o comprimento da base for de ?
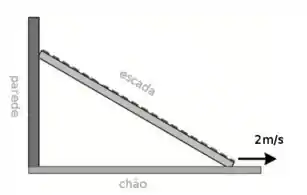
Como relacionar essas variáveis do deslocamento das pontas da escada??
Repare que em nenhum momento foi dada a equação que precisamos usar no problema, mas, como a escada faz um triângulo retângulo quando apoiada na parede, podemos considerar a altura e a base e usar Pitágoras para relacionar tudo:
Queremos saber também a variação da altura, portanto . Vamos derivar a equação implicitamente:
A base aumenta então e também .
Assim, quando :
Substituindo tudo:
Encontramos a variação da altura da escada, que é negativa, porque a escada está caindo.
Então é isso. Fique esperto! Apareceu triângulo retângulo, provavelmente você usará Pitágoras.
Perímetros, áreas e volumes
Além dos problemas envolvendo o teorema de Pitágoras, também são comuns aqueles que envolvem perímetros, áreas e volumes. Aí é só se ligar nas principais áreas e volumes cobrados.
Aqui a gente te apresenta as fórmulas de outras áreas recorrentes:
Os principais volumes que você precisa saber:
Além disso tudo, lembre-se que a vazão é variação do volume no tempo ().
Achando ângulos
Vamos repensar o problema da escada caindo:
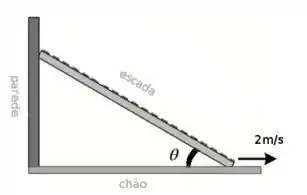
Qual a velocidade que altura diminui quando a velocidade angular de é de e ? Como descrever ângulo em relação a distâncias??
Trigonometria! Pegamos ali o seno, considerando a altura, então queremos saber .
Com:
Obs.: o sinal de “menos” na derivada significa que o ângulo está diminuindo em magnitude;)
Substituindo tudo:
Outras relações importantes que você precisa saber:
Lei dos cossenos e Lei dos Senos:
Soma de senos e cossenos:
Perímetros, áreas e volumes
Achando ângulos
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – Lista do Jair, Taxas Relacionadas, Questão 7
Um balão eleva-se verticalmente do solo à razão de . Quando o balão está a do solo, passa exatamente sob ele um automóvel viajando à velocidade de . Com que velocidade varia, segundos após, a distância entre eles?
Passo 1
Vamos desenhar o problema:
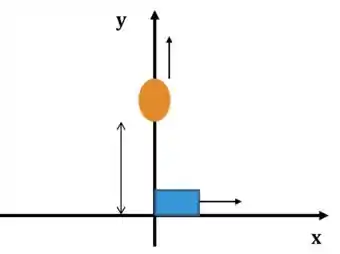
Agora a gente precisa determinar o que a gente tem que achar aí. O problema quer saber a variação da distância entre eles. Se a distância é então queremos saber:
Passo 2
Agora precisamos ver o que a gente tem. O balão se eleva verticalmente à razão de . Isso é a velocidade vertical. Se a posição é então:
Não se engane com relação a . O valor inicial de é . Para instantes seguintes teremos que:
No instante :
Temos também a velocidade do carro, que está andando horizontalmente. Sendo a posição horizontal:
O que vai relacionar isso tudo? Pitágoras!
Substituindo tudo que a gente sabe:
Passo 3
E agora? Se o carro estava andando a então sua posição será:
No ponto que a gente quer:
E ? Quando :
Agora é só felicidade. Vamos substituir tudo:
Resposta
Exercício Resolvido #2
UFRJ – Cálculo 1 – P1 2010.2 – 3
No desenho, o ponto representa um objeto que se desloca sobre uma semicircunferência de raio , com velocidade constante . Em cada instante, é a distância de até o diâmetro .
Durante o movimento de subida, qual será a taxa de variação da distância no momento em que ela medir ?
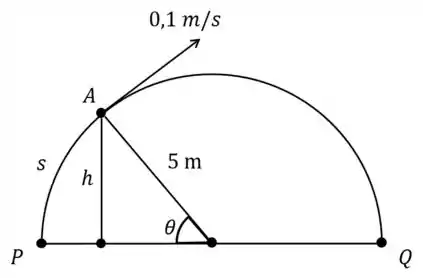
Passo 1
O que a questão pede é:
No instante em que m. O dado que nós temos é referente à velocidade.
Como a velocidade é a taxa de variação da posição com relação ao tempo, e o espaço percorrido pela partícula em é o arco , então é seguro dizer que a velocidade é:
Também temos o valor do raio da figura:
Passo 2
O que vai conectar os nossos e vai ser o ângulo que é comum aos dois:
Passo 3
Derivando em relação ao tempo:
Substituindo o que a gente já sabe na primeira:
Substituindo na segunda:
Passo 4
Agora basta achar quanto é o quando :
Da figura, temos, quando
Calculando essa felicidade:
Substituindo:
Resposta
Exercício Resolvido #3
UERJ - Cálculo 1 - Lista Derivadas – 4
Selecionado da Lista de Derivadas da Professora Renata - Cálculo 1 - UERJ
Um homem com de altura caminha em direção a um edifício, com uma velocidade de . Se existe um ponto de luz no chão a do edifício, com que velocidade a sombra do homem estará diminuindo, quando ele estiver a do edifício?
Passo 1
Vamos desenhando:
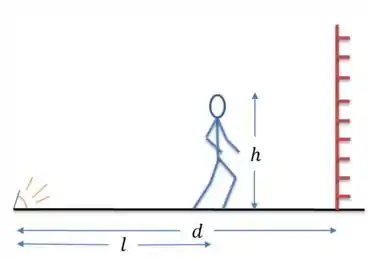
Bom, chamando a altura do cara de , a distância do ponto até a parede de e do ponto até o homem de . Repare, quando falamos na velocidade do cara, estamos, basicamente, falando da velocidade com que aumenta. Colocando, então tudo o que o cara me passou como dados, fica assim:
E ele quer saber, quando como varia a altura da sombra do maluco aí. Que é basicamente:
Passo 2
Vamos “matematicar” esse desenho:
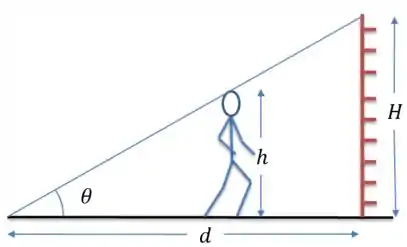
Onde a sombra tem altura . Repara que a inclinação que marcamos ali varia, é maior quando ele está mais perto do ponto e menor quando ele se afasta. O que não muda é essa relação entre as alturas e as distâncias que, por Semelhança de Triângulos, fica desse jeito:
Bom, pegando aquilo que já conhecemos, podemos deixar o em função do :
Passo 3
Repara no seguinte, tanto a altura quando a distância variam com o tempo. Se derivarmos em relação ao tempo ambas grandezas, podemos construir uma relação entre as taxas:
Queremos essa taxa quando ele estiver a da parede vamos ter:
Assim
Sabendo ainda que a taxa de variação vale, em qualquer momento, a mesma coisa:
Substituindo, portanto:
E é isso!
Resposta
Exercício Resolvido #4
UFRJ - Lista do Jair, Taxas Relacionadas, Questão 3
Um retângulo possui lados que variam com o tempo e está inscrito numa região triangular conforme a figura abaixo. Determine com que taxa a área do retângulo está variando no instante em que sua altura mede e está aumentando à taxa de . Neste instante a área está aumentando ou diminuindo?
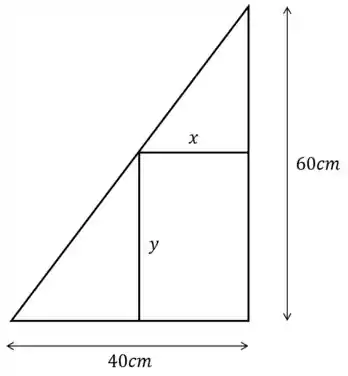
Passo 1
O problema quer saber a taxa com que a área do retângulo varia. Então ele quer:
Ele também nos disse que para o instante tratado, e
Passo 2
Podemos usar a expressão da área do retângulo para relacionar as variáveis do problema:
A expressão da área é:
Precisamos então derivar:
Substituindo o que a gente já sabe:
Passo 3
Precisamos de sua derivada. Mas temos que, por semelhança de triângulos:
Derivando ambos os lados:
Substituindo:
No momento em que a altura vale , temos:
Portanto, substituindo de volta na fórmula de :
Resposta
A taxa de variação da área é negativa e, portanto, a área do retângulo está diminuindo.
Exercício Resolvido #5
UFRJ - Cálculo 1 - P1 2015.1 – 3
Um cilindro circular reto está inscrito em uma esfera. Se o raio da esfera cresce a uma taxa de e o raio da base do cilindro cresce a uma taxa de , com que razão está variando a área lateral do cilindro no momento em que o raio da esfera é e o raio da base do cilindro é de ?
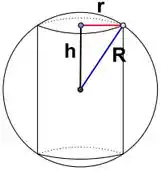
Passo 1
O que a gente quer achar? Queremos calcular a variação da área lateral do cilindro:
Chamando, como na figura, de o raio da esfera, o do cilindro e a metade da altura, vamos reunir aqui os dados num instante dado que eu vou chamar de :
Passo 2
E ele quer saber, com isso, como varia a área lateral do cilindro. Bom, podemos calcular essa área pela definição geométrica dela, que é a seguinte:
Porém, é uma variável da qual não conhecemos a taxa de variação e o valor em , o que complica para trabalhar. Por outro lado, dá para ver pela própria figura que e formam um triângulo retângulo, então poderemos escrever em função de e :
Substituindo:
Passo 3
Vamos derivar os dois lados em função do tempo e ver como ficamos (não se esqueça da regra do produto, heim):
Derivando a raiz e aplicando a regra da cadeia...
Bom, em a gente sabe quais serão os valores de , , e .
Agora é só substituir tudo o que temos mesmo...
Resposta
Exercício Resolvido #6
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 239-38
Dois navios a vapor estão navegando para longe de um ponto em rotas que forma um ângulo de . O navio desloca-se a 14 nós (milhas náuticas por hora). O navio desloca-se a 21 nós. A que taxa os navios estão se afastando entre si, quando e milhas náuticas?
Passo 1
Vamos tentar visualizar o problema:
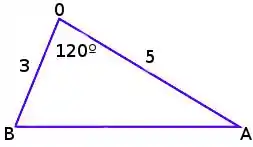
Queremos achar a variação da distância entre os navios que é descrita por :
Temos a informação das distancias e :
E as variações dessas distâncias (velocidades):
Sendo 1 nó igual à 1 milha náutica por hora.
Passo 2
Agora, o que relaciona isso tudo? Não dá para usar Pitágoras, pois não temos um triângulo retângulo. Que nos salvará agora será a lei dos cossenos:
Derivando isso tudo em relação ao tempo:
Substituindo tudo que a gente já sabe:
Falta só achar que achamos tudo que queremos.
Passo 3
Da lei dos cossenos:
Substituindo:
Ignoramos a parte negativa, pois é unidade de distância.
Substituindo:
Isolando:
Ficou um resultado bem feio, eu sei. Mas não se preocupe com isso, é bastante comum, até em prova, os resultados saírem assim.