Teorema De Rolle e Teorema Do Valor Médio
Teoria
Fala aí! Hoje vamos aprender sobre o Teorema de Rolle e o Teorema do Valor Médio. Nessa ordem, porque o segundo pode ser visto como uma aplicação do primeiro, beleza?
Vem comigo!
⭐ Veja também ⭐
O que é o Teorema de Rolle?
O Teorema de Rolle fornece uma condição suficiente para que exista pelo menos um ponto crítico em um intervalo
Esse teorema nos diz o seguinte:
Seja
Muito confuso esse tanto de palavra complicada que apareceu aí? Deixa eu desenhar pra ficar mais claro.
Imagine que
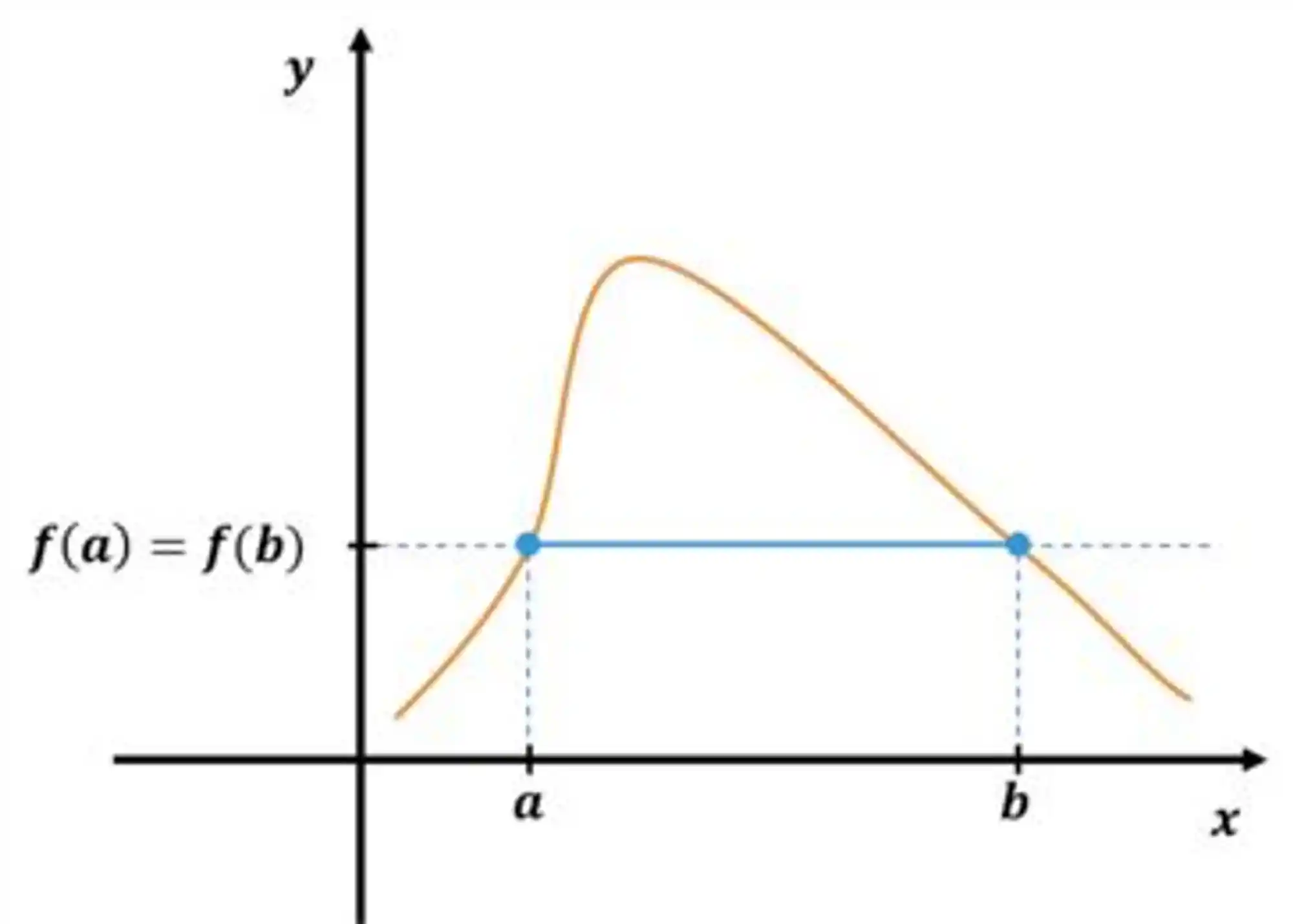
Ela é contínua e não constante, concorda? Além disso, repara como os pontos com
Para que isso ocorra, se em algum momento entre
Basicamente, é isso aí que o Teorema de Rolle tá falando, só que em termos mais matemáticos 😅
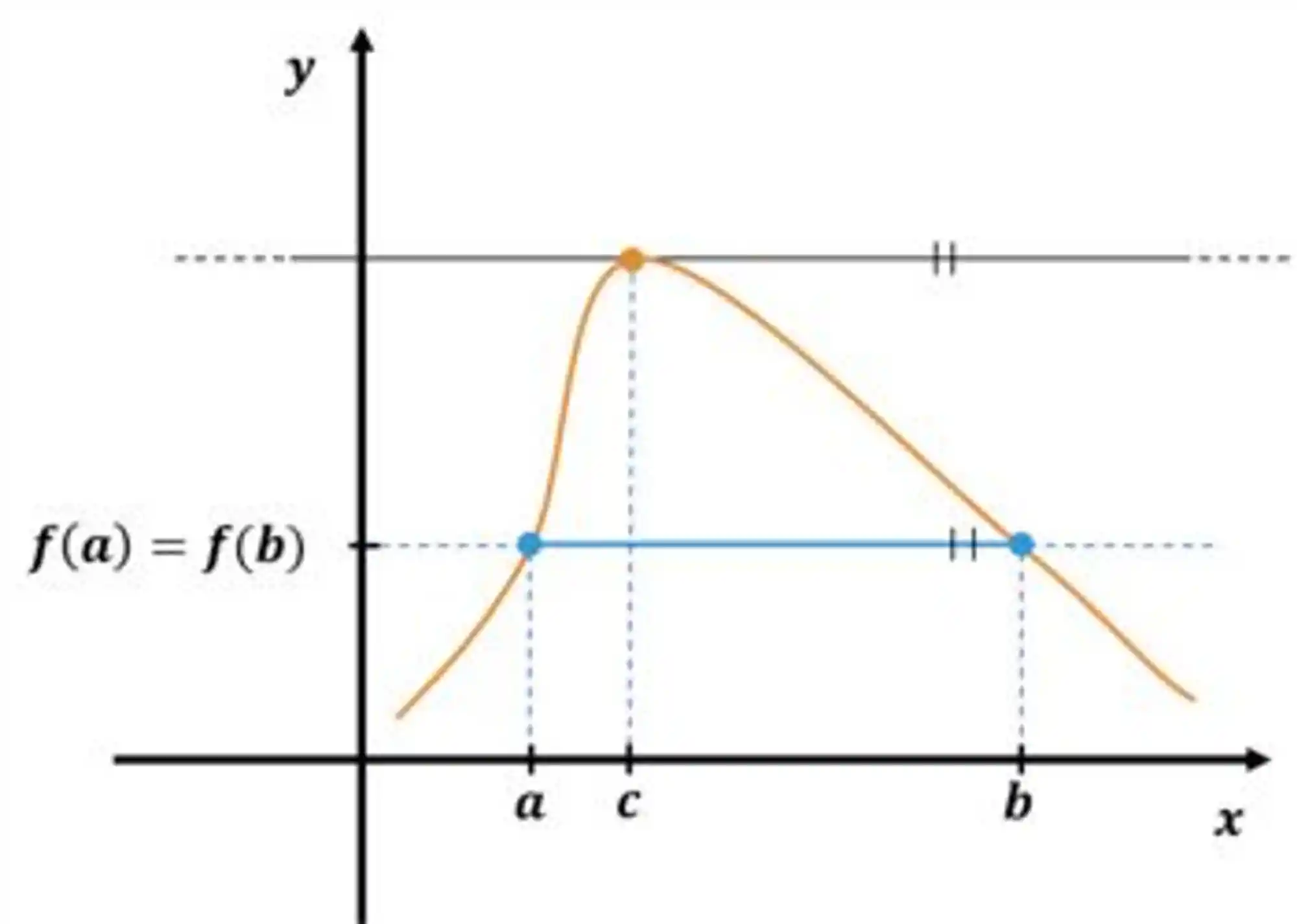
Demonstração do Teorema de Rolle
Pensa aqui comigo: se
Tá, agora, se
Suponha
Teorema do Valor Médio
Lembra que falei que esse aqui é bem parecido com o anterior?
O Teorema do Valor Médio segue as mesmas condições do Teorema de Rolle, a diferença é que agora não tem mais a restrição de que
Seja
Nossa, mas que que isso aí tem a ver com o outro teorema lá?
Te mostro agora! Olha só, vamos pegar aquele gráfico lá de cima e incliná-lo um pouquinho, assim:
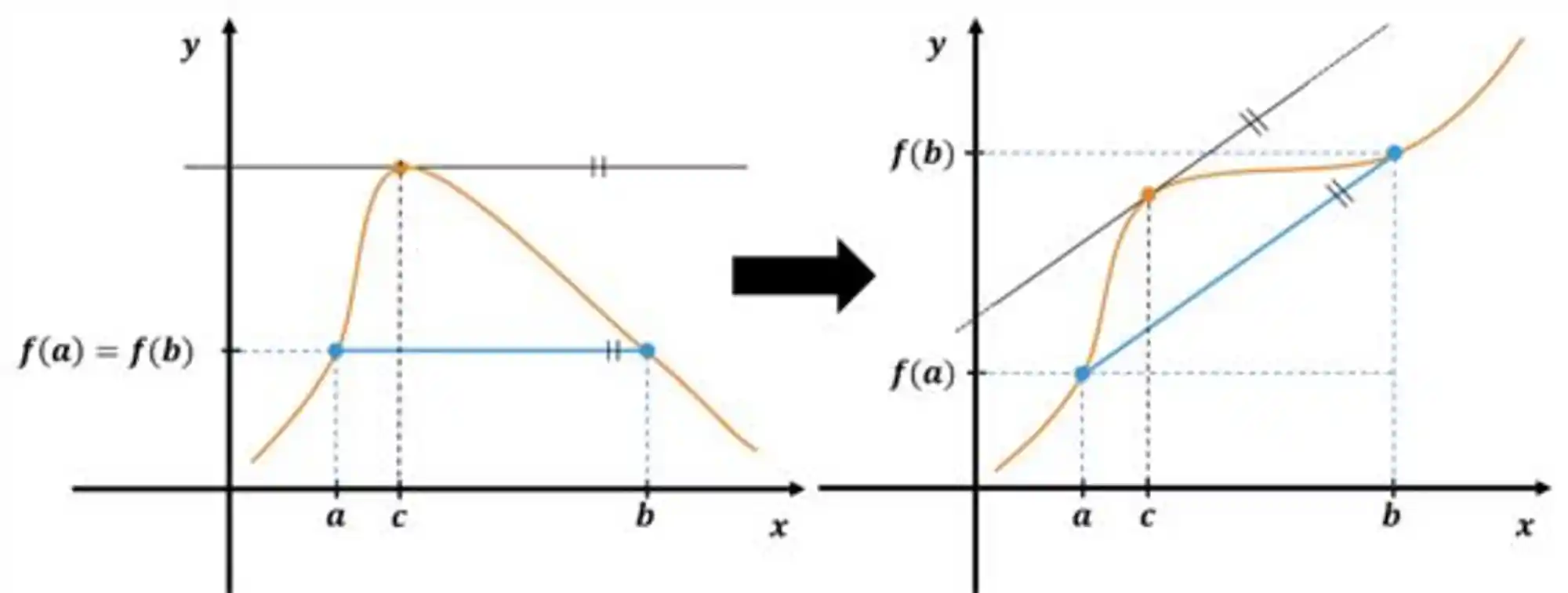
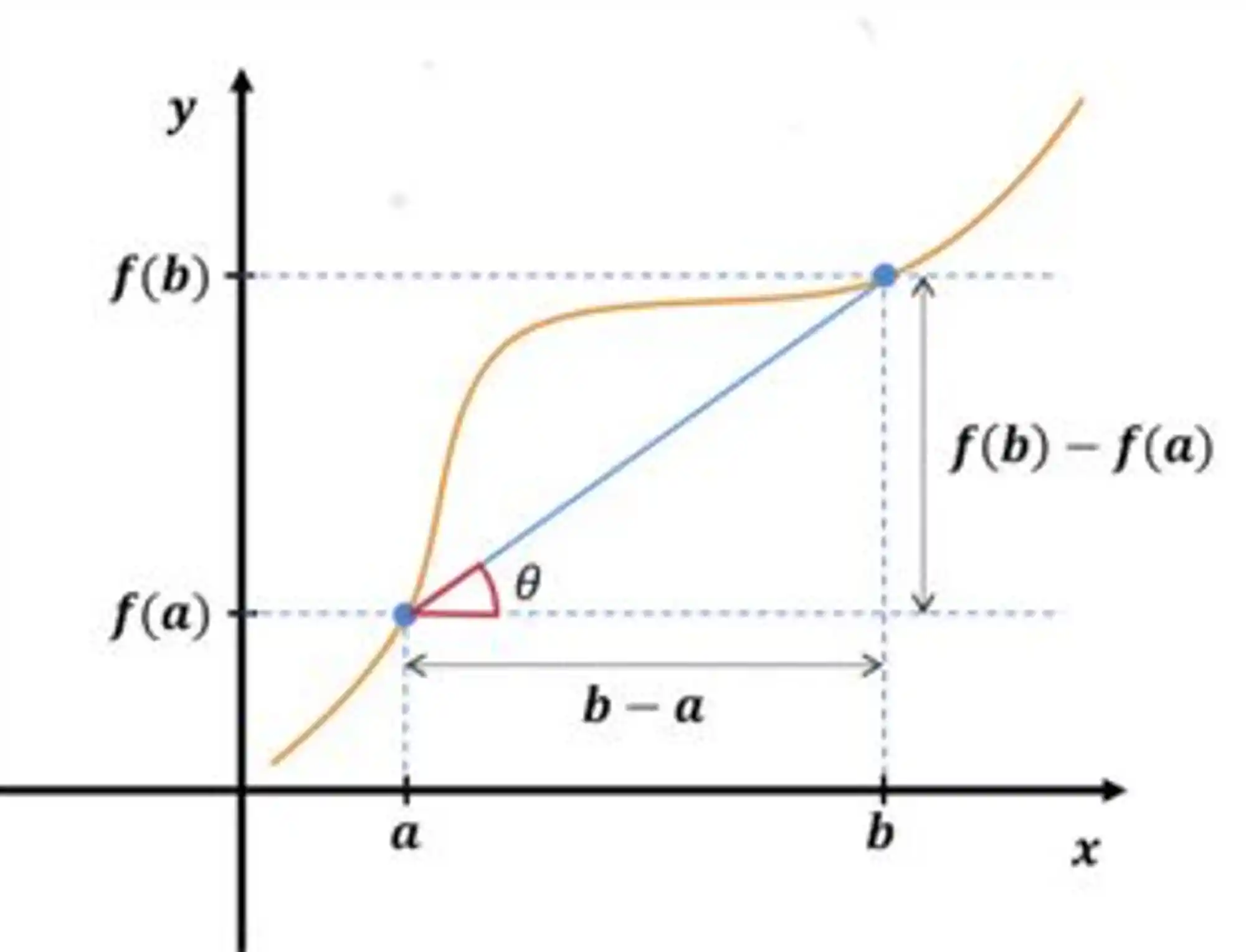
Então, a gente pode escrever o seguinte:
Essa fórmula aí pode ser interpretada fisicamente da seguinte forma: o lado direito da equação é a variação média de
Ah, olha só que interessante! Se
Que é o próprio Teorema de Rolle!
Bora finalizar com um exemplo?
Exemplo: Mostre que
Beleza, pra começar, vamos ver se podemos usar o Teorema aqui, né?
Primeiro, essa função é contínua?
Sim! Como ela é uma função polinomial, é contínua para qualquer valor de
Segundo, ela é derivável no intervalo?
Sim! Novamente, toda função polinomial é derivável.
Ok, então vamos verificar se
Condição satisfeita!
Quer dizer que existe um valor
Quem é
Só derivar aquela funçãozinha clássica dada pelo enunciado.
Aí é só substituir
Dá só uma olhada no gráfico dessa função:
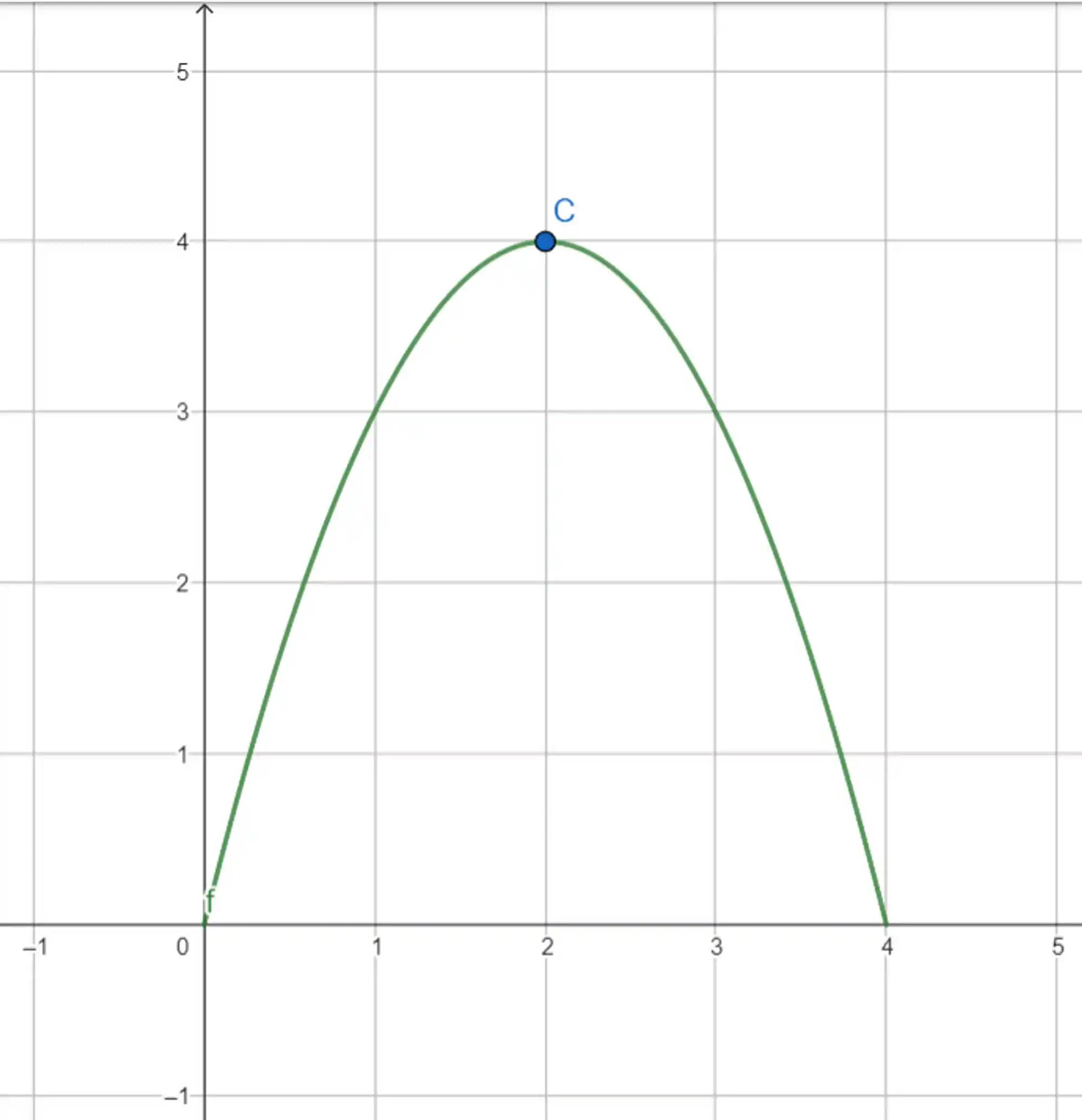
O ponto crítico no intervalo é exatamente o que calculamos!
Teorema do Valor Médio
Exemplo: Mostre que tem um ponto crítico no intervalo usando o Teorema de Rolle.
Exercícios Resolvidos
Exercício Resolvido #1
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 284-9.
A função:
é zero quando e e derivável em, mas sua derivada em nunca é zero. Explique por quê. O teorema de Rolle não diz que a derivada deveria ser zero em algum lugar em ? Justifique sua resposta.
Passo 1
Pelo teorema de Rolle temos que:
Repara que para a gente poder aplicar o Teorema de Rolle, antes temos que ver se essas duas condições são satisfeitas:
- A função é contínua para todo o intervalo fechado .
- A função é derivável para todo o intervalo aberto .
Passo 2
Vamos começar avaliando se a função é contícua no intervalo fechado .
Repara que a nossa função muda de cara quando chegamos na fronteira . Deste modo, vamos testar a contínuidade na fronteira.
Lembra do capítulo de continuidade? Então, a função será contínua no ponto se os limites laterias forem iguais a função no ponto:
A função no ponto a gente já sabe,
Agora vamos avaliar o limite pela esquerda (ou seja, para valores menores que 1)
Opa! Repara o limite lateral não é igual a função no ponto. Em outras palavras,
Ou seja, essa função não é contínua, logo o teorema não é aplicável.
Resposta
A função não satifaz as hipóteses do teorema de Rolle, pois ela não é contínua.
Exercício Resolvido #2
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 284-6 - MODIFICADO.
A função abaixo satisfaz as hipóteses do teorema do valor médio no intervalo dado? Justifique sua resposta.
Passo 1
Legal, temos, à esquerda da vírgula, a função a analisar e, à direita, o intervalo.
Para ver se a função satisfaz as hipóteses do teorema do valor médio temos que garantir que:
- A função seja contínua para todo o intervalo fechado .
- A função seja derivável para todo o intervalo aberto .
Passo 2
A função é uma função potência, que é contínua para todo . Assim, garantimos a primeira condição.
Passo 3
A derivada dessa função, segue a regra da derivação de funções potência, onde:
Essa derivada não vai existir para , pois teremos uma divisão por zero. Isso não é problema, pois precisamos somente que a função seja derivável para intervalo aberto , ou seja, ela não precisa ser derivável nas fronteiras do intervalo, em . e .
Dessa maneira, a função satifaz as hipóteses do TVM.
Resposta
A função satifaz as hipóteses do TVM. Justificativa no desenvolvimento.
Exercício Resolvido #3
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 284-8 - MODIFICADO.
A função abaixo satisfaz as hipóteses do teorema do valor médio no intervalo dado? Justifique sua resposta.
Passo 1
Agora o intervalo a analisar é o intervalo definido da função, ou seja, .
Para ver se a função satisfaz as hipóteses do teorema do valor médio temos que garantir que:
- A função seja contínua para todo o intervalo fechado .
- A função seja derivável para todo o intervalo aberto .
Passo 2
A função está definida para . Pois não acontece nenhuma divisão por zero, raiz ou log negativos nesse ponto.
O problema vem em , onde teremos que testar a contínuidade da função. Lembra do capítulo de continuidade? Então. A função será contínua nesse ponto se:
Sabendo que, por limite fundamental:
E:
Como o limite lateral é diferente do valor da função no ponto ela é descontinua.
Com isso, a gente concluí que, infelizmente, a função não cumpre os requisitos do TVM.
“Eu teria escapado se não fossem essas crianças.” –
Resposta
A função não satifaz as hipóteses do TVM. Justificativa no desenvolvimento.