Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Elipsóide, Esfera e Hiperbolóides

Ver Todos os Exercícios

Teoria

Equações:

Fala, rapaziada! Hoje vamos tratar de superfícies quádricas. Dividimos elas em dois grupos para gente poder estuda-las com calma e deixar tudo bem explicadinho pra você.

O grupo que vamos estudar agora, tem a seguinte forma:

± x - x 0 2 a 2 ± y - y 0 2 b 2 ± z - z 0 2 c 2 = 1

a , b , c > 0

Calma que eu já explico!

Elipsoide

Quando os 3 sinais forem positivos . A fórmula geral do Elipsoide com centro em ( x 0 , y 0 , z 0 ) é :

x - x 0 2 a 2 + y - y 0 2 b 2 + z - z 0 2 c 2 = 1

Caso o Elipsoide tenha centro em ( 0,0 , 0 ) a equação fica:

x 2 a 2 + y 2 b 2 + z 2 c 2 = 1

O gráfico do Elipsoide tem a forma:

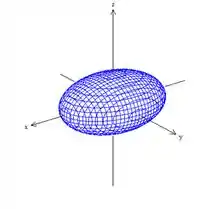
Observação: Para o caso de a = b = c temos uma esfera de raio r = a

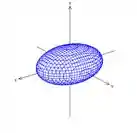
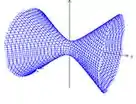
Hiperbolóide de uma folha:

Quando temos 2 sinais positivos e 1 é negativo. As equações do Hiperbolóide de uma folha são:

x - x 0 2 a 2 + y - y 0 2 b 2 - z - z 0 2 c 2 = 1

x - x 0 2 a 2 - y - y 0 2 b 2 + z - z 0 2 c 2 = 1

- x - x 0 2 a 2 + y - y 0 2 b 2 + z - z 0 2 c 2 = 1

Seus gráficos são respectivamente:

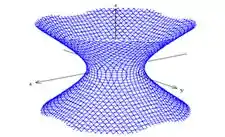
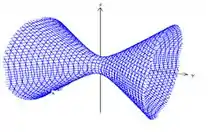
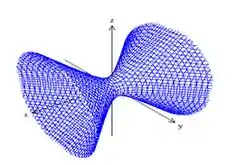
Perceba que eixo do Hiperbolóide de uma folha encontra-se ao longo do eixo da variável com sinal negativo.

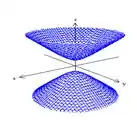
Hiperbolóide de duas folhas:

Quando apenas 1 sinal é positivo e 2 sinais são negativos. As equações do Hiperbolóide de duas folhas são:

x - x 0 2 a 2 - y - y 0 2 b 2 - z - z 0 2 c 2 = 1

- x - x 0 2 a 2 - y - y 0 2 b 2 + z - z 0 2 c 2 = 1

- x - x 0 2 a 2 + y - y 0 2 b 2 - z - z 0 2 c 2 = 1

Seus gráficos são respectivamente:

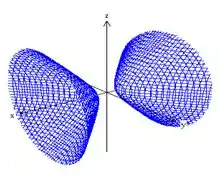
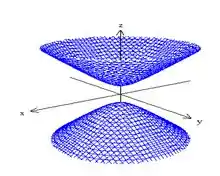
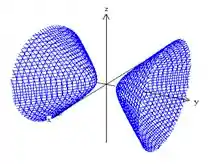
Perceba que o eixo do hipérbolóide de duas folhas ocorre ao longo do eixo da variável com sinal positivo.

Exemplo:

Identifique a quádrica a seguir:

x 2 4 + x 2 + y 2 - 2 y + z 2 + 1 4 = 0

Qual dos seguintes gráficos mais se assemelha a ela?

Resolução:

Que parada bizarra é essa ???

x 2 4 + x 2 + y 2 - 2 y + z 2 + 1 4 = 0          

Calma, acredite em mim, isso é uma quádrica. Vou provar pra você.

Primeiramente, observe que todas as variáveis elevadas ao quadrado tem coeficientes positivos. Isso nos indica possivelmente um Elipsoide.

Para provar que é um elipsoide ,vamos ver se conseguimos colocar essa equação na forma:

x - x 0 2 a 2 + y - y 0 2 b 2 + z - z 0 2 c 2 = 1

Primeiramente vamos olhar para:

x 2 4 + x 2

Vamos tentar ajeitá-lo, para que ele fique da forma de um quadrado perfeito

x 2 4 + x 2 = x 2 + 2 x 4  

Opa! O numerador nos faz lembrar x + 1 2 = x 2 + 2 x + 1 . Mas não tem esse " + 1 " no numerador. Podemos fazer o seguinte:

x 2 4 + x 2 = x 2 + 2 x 4 = x 2 + 2 x + 1 - 1 4 = x + 1 2 - 1 4 = x + 1 2 4 - 1 4

Sacou? Eu somei 1   e subtraí 1 do numerador, para que aparecesse o quadrado perfeito.

Observação: Perceba que x 2 + a x = x + a 2 2 - a 2 4 , no caso acima: x 2 + 2 x = x + 1 2 - 1

Vamos fazer a mesma análise para o termo :

y 2 - 2 y

Esse termo nos lembra:

y - 1 2 = y 2 - 2 y + 1

Ajeitando temos:

y 2 - 2 y = y 2 - 2 y + 1 - 1 = y - 1 2 - 1

Portanto, a equação ( i ) fica:

x 2 4 + x 2 + y 2 - 2 y + z 2 + 1 4 = 0          

x + 1 2 4 - 1 4 + y - 1 2 - 1 + z 2 + 1 4 = 0 → x - ( - 1 ) 2 4 + y - 1 2 + z 2 = 1

Que é exatamente a equação do elipsoide!!! Letra A!!!!!!

Obtendo gráficos

Agora que já vimos as equações e a “cara” do gráfico das superfícies quádricas, vamos mostrar porque elas são assim e esboçar seus gráficos passo a passo.

Vou te mostrar o passo a passo com esse exemplo aqui

x 2 4 + y 2 9 + z 2 16 = 1

Sabemos que isso é uma elipsoide. Ele vai ter mais ou menos a cara:

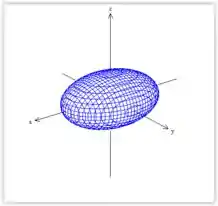
Vamos começar esboçando seus traços, ou seja, a interseção do Elipsóide com os planos coordenados.

Traços:

  • Traço no plano x y   z = 0 :

    • x 2 4 + y 2 9 = 1

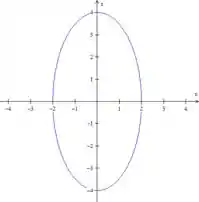
    É uma elipse com centro em ( 0,0 , 0 ) e semi-eixos 2 e 3. O traço fica:

  • Traço no plano x z   ( y = 0 ) :

    • x 2 4 + z 2 16 = 1

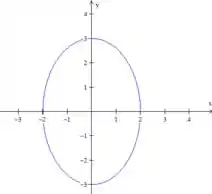
    É uma elipse com centro em ( 0,0 , 0 ) e semi-eixos 2 e 4. O traço fica:

  • Traço no plano y z   ( x = 0 ) :

    • y 2 9 + z 2 16 = 1

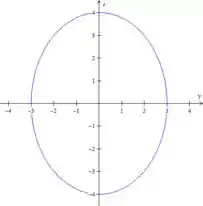
    É uma elipse com centro em ( 0,0 , 0 ) e semi-eixos 3 e 4. O traço fica:

    Vamos fazer agora interseções com planos paralelos aos eixos coordenados.

    Interseções:

  • Plano z = k

    • x 2 4 + y 2 9 = 1 - k 2 16 → x 2 4 1 - k 2 16 + y 2 9 1 - k 2 16 = 1

    São elipses para - 4 < k < 4

    Observação: Para k > 4 ou k < - 4 repare que 1 - k 2 16 < 0 , logo não existe x e y que satisfaçam: x 2 4 + y 2 9 = 1 - k 2 16 < 0 , pois a soma de dois números elevados ao quadrado não pode ser menor do que zero. Por isso, não há interseção k > 4 ou k < - 4

  • Plano y = k

    • x 2 4 + z 2 16 = 1 - k 2 9 → x 2 4 ( 1 - k 2 9 ) + z 2 16 ( 1 - k 2 9 ) = 1

    São elipses para - 3 < k < 3

  • Plano x = k

y 2 9 + z 2 16 = 1 - k 2 4 → y 2 9 ( 1 - k 2 4 ) + z 2 16 ( 1 - k 2 4 ) = 1

São elipses para - 2 < k < 2

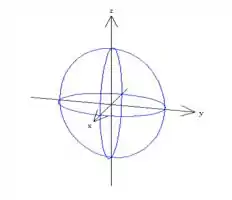
Agora no seu gráfico plote os traços que achamos

Agora é só achurar aregião delimitada pelos traços

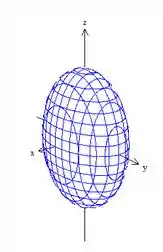
Esse raciocínio é o que você precisa saber para esboçar qualquer superfície. Eu fiz um exemplo para te mostrar o jeitão desses exercícios. Agora é com você! Vai lá nos exercícios praticar um pouco.

Hiperbolóide de uma folha:

Hiperbolóide de duas folhas:

Exemplo:

Obtendo gráficos

Exercícios Resolvidos

Exercício Resolvido #1

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 217 – 1,2,8,12

Associe cada quádrica ao gráfico que mais se assemelha a ela:

  1. x 2 + y 2 + 4 z 2 = 10
  2. z 2 + 4 y 2 - 4 x 2 = 4
  3. z 2 + x 2 - y 2 = 1
  4. 9 x 2 + 4 y 2 + 2 z 2 = 36

i)

ii)

iii)

iv)

v)

Passo 1

Antes de começar, só um obszinho: tem 5 figuras e 4 opções apenas, estranho, né? Mas é que alguma opção de superfície vai se aplicar a mesma figura, ou seja, uma mesma figura vai estar associada a mais de uma superfície. Pode parecer estranho a questão fazer isso, mas a ideia era só ver se a gente conhece a “cara” das superfícies.

Sem mais delongas, vamos lá: devemos observar os sinais dos coeficientes que estão multiplicando as variáveis elevadas ao quadrado.

  1. 3 coeficientes positivos, isso indica uma elipsoide
  2. 2 coeficientes positivos, indica uma hiperboloide de uma folha
  3. 2 coeficientes positivos, indica uma hiperboloide de uma folha
  4. 3 coeficientes positivos, isso indica uma elipsoide

Passo 2

Devemos agora conseguir colocar as equações das quádricas na forma geral de cada uma delas, para termos certeza que são essas quadricas mesmo.

  1. x 2 + y 2 + 4 z 2 = 10 , dividindo por 10 temos: x 2 10 + y 2 10 + z 2 10 4 = 1 isso confirma que trata-se de um elipsoide.
  2. z 2 + 4 y 2 - 4 x 2 = 4 → z 2 4 + y 2 - x 2 = 1 , é um hiperboloide de uma folha
  3. z 2 + x 2 - y 2 = 1 , é um hiperboloide de uma folha
  4. 9 x 2 + 4 y 2 + 2 z 2 = 36 → x 2 4 + y 2 9 + z 2 18 = 1 é um elipsoide

Passo 3

Agora vamos correlacionar as quádricas já identificadas com seu esboço

  1. É um elipsoide, portanto a única alternativa possível é a i)
  2. É um hiperboloide de uma folha com o coeficiente de x 2 negativo. Seu gráfico só pode ser a alternativa iii)
  3. É um hiperboloide de uma folha com o coeficiente de y 2 negativo. Seu gráfico só pode ser a alternativa ii)
  4. É um elipsoide, portanto a única alternativa possível é a i)

Resposta

  1. Elipsoide, figura i)
  2. Hiperboloide de uma folha, figura iii)
  3. hiperboloide de uma folha, figura ii)
  4. Elipsoide, figura i)

Exercício Resolvido #2

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 169 - 50

Encontre o centro e o raio da esfera:

x 2 + y 2 + z 2 - 6 y + 8 z = 0

Passo 1

Nesse tipo de questão, temos de completar quadrados para colocar a equação dada na forma padrão da esfera.

Observe o termo y 2 - 6 y . Ele nos faz lembrar y - 3 2 , ajeitando temos:

y 2 - 6 y = y - 3 2 - 9

Observe o termo z 2 + 8 z . Ele nos faz lembrar z + 4 2 , ajeitando temos:

z 2 + 8 z = z + 4 2 - 16

Portanto, a equação fornecida no enunciado fica:

x 2 + y 2 + z 2 - 6 y + 8 z = 0

x 2 + y - 3 2 - 9 + z + 4 2 - 16 = 0

x 2 25 + y - 3 2 25   + z + 4 2 25 = 1

Passo 2

Agora basta identificar que a esfera tem raio 5 e centro em 0,3 , - 4

Resposta

A esfera tem centro em 0,3 , - 4 e raio 5

Exercício Resolvido #3

UFRJ - Cálculo 2 - P1 2008.1 - 4ª

Seja a quádrica cuja equação cartesiana é dada por 2 x 2 + y 2 + 2 y + z 2 = 9 .

Identifique a quádrica.

Passo 1

Identificar a quádrica:

A equação da quádrica tem termos y 2 e y .

Portanto, precisamos completar quadrados:

y 2 + 2 y + b 2 = a 2 + 2 a b + b 2

Comparando termo a termo:

a 2 = y 2 2 a b = 2 y b 2 = b 2

Resolvendo o sistema, encontramos que:

a = y   b = 1

Passo 2

Voltando à equação da quádrica e somando b 2 = 1 nos dois lados:

2 x 2 + y 2 + 2 y + 1 ⏟ y + 1 2 + z 2 = 9 + 1

⇒ 2 x 2 + y + 1 2 + z 2 = 10

Dividindo tudo por 10 :

x 2 5 + y + 1 2 10 + z 2 10 = 1

Logo, essa quádrica é um elipsoide com centro em ( 0 ,   - 1 ,   0 ) .

Resposta

Elipsoide com centro em ( 0 ,   - 1 ,   0 ) .

Exercício Resolvido #4

UFRJ - Cálculo 2 - P1 2011.1 - 4ª

S 1 :   - 9 x 2 - 9 z 2 + 36 y 2 = 36 e S 2 :   - 2 x 2 + z 2 + 4 y 2 = 4

Identifique e esboce as superfícies S 1 e S 2 .

Passo 1

Identificar S 1 :

- 9 x 2 - 9 z 2 + 36 y 2 = 36

⇒ - x 2 4 - z 2 4 + y 2 = 1

Temos dois sinais negativos:

Logo, a superfície é um hiperboloide de duas folhas e o eixo está em y , pois é o termo positivo na equação.

Passo 2

Esboço de S 1 :

Passo 3

Identificar S 2 :

- 2 x 2 + z 2 + 4 y 2 = 4

⇒ - x 2 2 + z 2 4 + y 2 = 1

Temos um sinal negativo:

Logo, a superfície é um hiperboloide de uma folha e o eixo está em x , pois é o termo negativo na equação.

Passo 4

Esboço de S 2 :

Resposta

S 1 é hiperboloide de duas folhas.

S 2 é hiperboloide de uma folha.

Esboços:

Exercício Resolvido #5

UFRJ - Cálculo 2 - P1 2008.2 - 4.1

Considere a superfície S em R 3 dada pela equação x 2 - 2 x + y 2 + z 2 - 4 z = 6 .

Identifique a superfície quádrica S e desenhe a figura correspondente a essa quádrica.

Passo 1

Identificar a quádrica:

A equação da quádrica tem termos x 2 e x , e z 2 e z .

Portanto, precisamos completar quadrados:

x 2 - 2 x + b 2 = a 2 + 2 a b + b 2

Comparando termo a termo:

a 2 = x 2 2 a b = - 2 x b 2 = b 2

Resolvendo o sistema, encontramos que:

a = x   b = - 1

Fazendo o mesmo para a variável z :

z 2 - 4 z + b 2 = a 2 + 2 a b + b 2

Comparando termo a termo:

a 2 = z 2 2 a b = - 4 z b 2 = b 2

Resolvendo o sistema, encontramos que:

a = z   b = - 2

Voltando à equação da quádrica e somando as devidas parcelas nos dois lados:

x 2 - 2 x + 1 ⏟ x - 1 2 + y 2 + z 2 - 4 z + 4 ⏟ z - 2 2 = 6 + 1 + 4

⇒ x - 1 2 + y 2 + z - 2 2 = 11

Logo, essa quádrica é uma esfera com centro em ( 1 ,   0   , 2 ) .

Passo 2

- ''

Resposta

Esta quádrica é uma esfera com centro em ( 1 ,   0   , 2 ) :

Exercícios de Livros Relacionados

Os Exercícios 25 e 26 nos dão informações sobre os focos e vértices das elipses centradas na origem do plano xy. Em cada um dos casos, encontre a equação na forma padrão da elipse a partir das informa
Os Exercícios 49-52 fornecem equações para elipses e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada elipse deve ser deslocada. Encontre uma equação para a
Os Exercícios 27-34 fornecem equações para hipérboles. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu e
Os Exercícios 53-56 fornecem equações para hipérboles e nos dizem quantas unidades para cima ou para baixo e para a direita ou para a esquerda cada hipérbole deve ser deslocada. Encontre uma equação p
Os Exercícios 27-34 fornecem equações para hipérboles. Coloque cada equação na forma padrão e encontre as assíntotas da hipérbole. Em seguida, esboce a hipérbole. Inclua as assíntotas e focos no seu e