Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Cone e Parabolóides

Ver Todos os Exercícios

Teoria

Fala aí! Seja bem vindo ao Responde Aí! Bora conversar sobre Paraboloides e Cones?!

Paraboloides

A paraboloide é uma superfície quadrática, elas são regiões formadas quando as cônicas se movimentam no espaço.

-Eu sei, definição esquisita! Mas não se prende a isso não, aqui a gente vai aprender na prática! A equação geral de uma paraboloide tem essa carinha aqui:

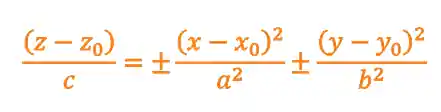
Equação geral de uma paraboloide
Equação geral de uma paraboloide

Existem dois tipos de paraboloides. Quando os sinais forem iguais temos um paraboloide elíptico, quando os sinais forem opostos temos um paraboloide hiperbólico!

Paraboloide Elíptico

E dentro das paraboloides elípticas existem várias variações dela! 🤣 Olha só esse quadro resumo:

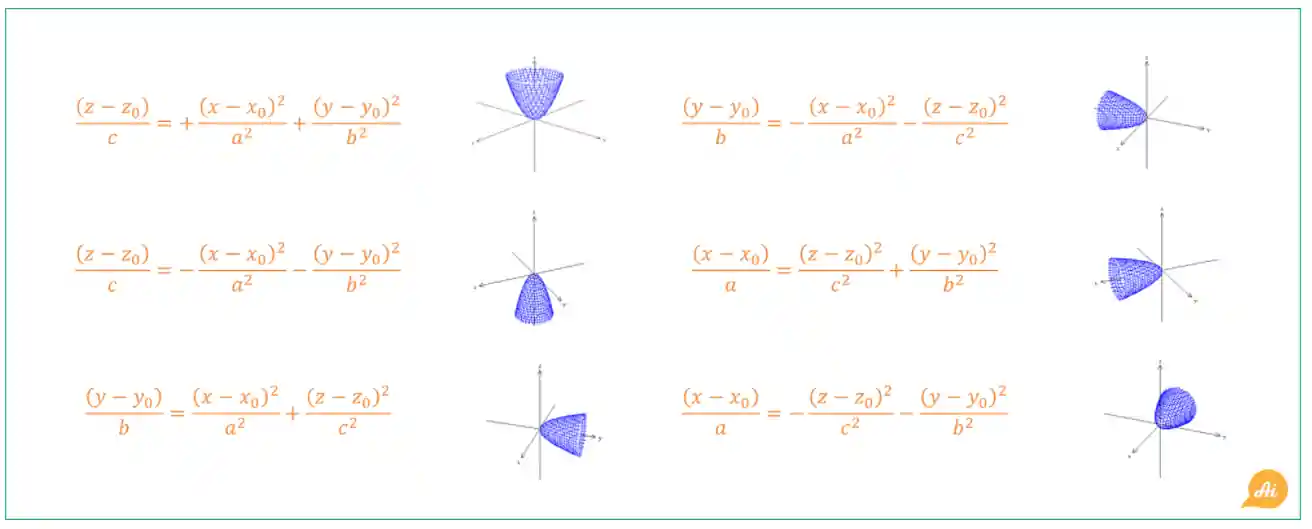
Paraboloides Elípticos e suas equações
Paraboloides Elípticos e suas equações

Nesse vídeo aqui em baixo a gente te explica tudo o que você precisa saber sobre Paraboloides e Cones e como elas podem cair aparecer nos exercícios! Dá só uma conferida! 😉

Paraboloide Hiperbólico

O paraboloide hiperbólico é o que tem o formato mais diferentão!

Paraboloides Hiperbólicos e suas equações
Paraboloides Hiperbólicos e suas equações

Repare que o gráfico é parecido com uma sela de cavalo. Logo, também é chamado de sela. Além disso, a sela é orientada da direção do eixo da variável de grau 1.


Ou seja, nos dois exemplos acima, imagine que alguém irá montar na sela. O corpo vai ficar na direção do eixo e as pernas da pessoa vão ficar na direção do eixo com sinal negativo, respectivamente e .

Cone Elíptico

O cone elíptico tem essa carinha simpática aqui:

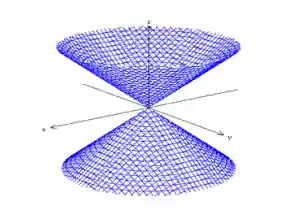
Cone elíptico
Cone elíptico

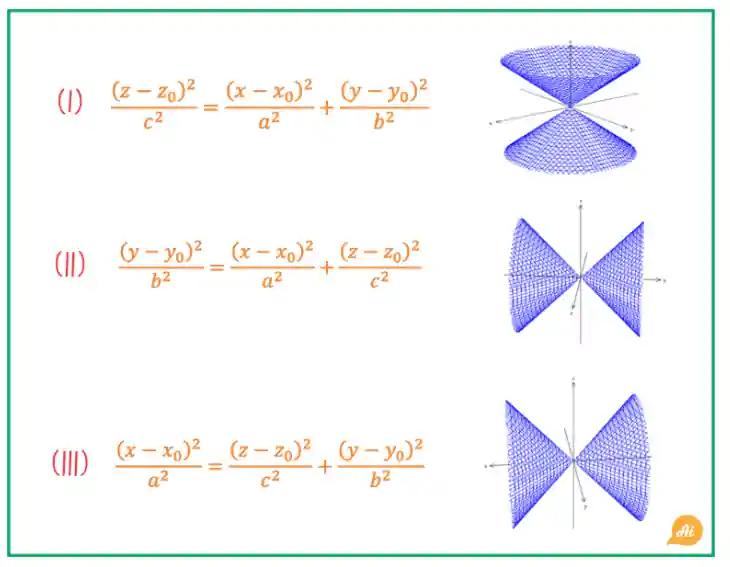
Mas quando você não tem o gráfico, pra identificar um cone elíptico você tem que ficar ligado em como é a carinha da sua equação geral:

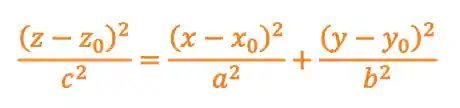
Equação geral de um cone elíptico
Equação geral de um cone elíptico

É claro que na prática essa equação pode aparecer um pouquinho diferente! Se liga em algumas variações do cone elíptico e suas equações:

Cones elípticos e suas equações
Cones elípticos e suas equações

Como Esboçar uma Superfície

Vamos, agora, aprender a como esboçar essas superfícies, através desse exemplo aqui:

Vamos começar esboçando seus traços, ou seja, a interseção do cone com os planos coordenados!

Passo 1: Traçar Planos

A primeira ciosa que precisamos fazer é traçar os planos!

  • Traço no plano xy (z=0)

    temos um ponto (0,0,0)

  • Traço no plano xz (y=0)

  • Traço no plano yz (x=0)

Passo 2: Estabelecer as intersecções

Vamos fazer agora interseções com planos paralelos aos eixos coordenados!

  • Plano
  • Plano
  • Plano

Agora no seu gráfico plote os traços que achamos, desenhe duas elipses ,que são as interseções com planos paralelos ao eixo z, uma no topo e outra na base inferior. Hachure a área compreendida entre as curvas. O gráfico será:

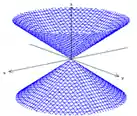
Gráfico plotado
Gráfico plotado

Esse é o passo a passo que você precisa saber para esboçar as superfícies! Fechou?! Bora praticar, galera!!!

Cone Elíptico

Como Esboçar uma Superfície

Exercícios Resolvidos

Exercício Resolvido #1

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON education do Brasil Ltda, 2009, pp. 217 – 4,5,6,9,10 e 11

Associe cada quádrica ao gráfico que mais se assemelha a ela:

  1. y 2 + z 2 = x 2
  2. y 2 - z 2 = x
  3. - z 2 - y 2 = x
  4. - 4 x 2 - y 2 = z
  5. x 2 + 4 z 2 = y 2

Passo 1

Primeiramente devemos observar o grau de cada variável e os sinais dos coeficientes que estão multiplicando-as.

y 2 + z 2 = x 2

já está na forma padrão da equação do cone circular. Repare que o eixo do cone é o eixo x pois é essa variável que está “isolada” na equação do cone. Portanto a melhor figura é a iv)

Passo 2

y 2 - z 2 = x

já está na forma padrão da equação do paraboloide hiperbólico(sela) pois temos uma variável com grau 1 de um lado da equação e do outro temos variáveis de grau 2 com sinais opostos.

Além disso, o eixo de grau 1 é o eixo x , imagine que se uma pessoa fosse montar nessa sela, seu corpo ficaria paralelo ao eixo x , e as pernas da pessoa ficariam ao longo do eixo com sinal negativo, eixo z . Portanto, figura ii)

Passo 3

- z 2 - y 2 = x

já está na forma padrão da equação do paraboloide elíptico, pois temos uma variável com grau 1 de um lado da equação e do outro temos variáveis de grau 2 com sinais iguais.

O eixo do paraboloide será o eixo x (variável de grau 1) , pegando a porção negativa, devido aos sinais negativos da equação. Figura v)

Passo 4

- 4 x 2 - y 2 = z → - x 2 - y 2 4 = z 4

Agora está na forma padrão da equação do paraboloide elíptico, pois temos uma variável com grau 1 de um lado da equação e do outro temos variáveis de grau 2 com sinais iguais.

O eixo do paraboloide será o eixo z (variável de grau 1) , pegando a porção negativa devido aos sinais negativos da equação. Figura iii)

Passo 5

x 2 + 4 z 2 = y 2 → x 2 4 + z 2 = y 2 4

Agora está na forma padrão da equação do cone elíptico, pois temos uma variável com grau 2 de um lado da equação e do outro temos variáveis de grau 2 com sinais iguais.

O eixo do cone será o eixo y (variável “separada”). Figura i)

Resposta

  1. Cone circular, figura iv)
  2. Parabolóide Hiperbólico, figura ii)
  3. Parabolóide Elíptico, figura v)
  4. Parabolóide Elíptico, figura iii)
  5. Cone Elíptico, figura i)

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 68 - 14.

Ache a superfície de ponto P = ( x , y , z ) , cuja distância ao eixo y é 2/3 da distância de P ao plano x z . Identifique a superfície.

Passo 1

O problema não fala diretamente em quádricas nessa questão. Bom, primeiramente vamos ilustrar geometricamente o que o problema nos informou. Chamando de D a distância de P ao eixo y temos:

Passo 2

Agora, podemos encontrar uma equação para D . Temos :

D 2 = x 2 + z 2 → D = x 2 + z 2 1 2

Passo 3

A distância de um ponto ao plano x z é a própria coordenada y do ponto.

O problema diz que a distância ao eixo y é 2/3 da distância ao plano x y . Então temos:

x 2 + z 2 1 2 = 2 3 y

x 2 + z 2 = 4 9 y 2

9 x 2 4 + 9 z 2 4 = y 2

Que é a equação do cone circular.

Resposta

Cone circular com equação:

9 x 2 4 + 9 z 2 4 = y 2

Exercício Resolvido #3

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 68 - 15.

Ache a superfície de ponto P = ( x , y , z ) tais que a distância de P ao ponto ( 0,0 , 1 ) é a mesma do que a de P ao plano y = - 1 .Identifique a superfície.

Passo 1

O problema não fala diretamente em quádricas nessa questão. Bom, primeiramente vamos encontrar a distância de P = ( x , y , z ) ao ponto ( 0,0 , 1 ) . Chamando essa distância de D temos:

D = x 2 + y 2 + z - 1 2 1 2  

Passo 2

Perceba que a distância do ponto P = ( x , y , z ) ao plano y = - 1 é compreendida como sendo a menor distância entre o ponto P e o ponto mais próximo a ele, pertencente ao plano.

Ou seja, é a projeção do ponto P no plano y = - 1 . Vamos chamar essa projeção do ponto P no plano y = - 1 de P ' .Perceba que P ' = ( x , - 1 , z ) . Geometricamente temos:

d 2 = x , y , z - x , - 1 , z 2 = 0 + y + 1 2 + 0 = y + 1 2

d = y + 1

Passo 3

Como D = d temos:

x 2 + y 2 + z - 1 2 1 2 = ( y + 1 )

x 2 + y 2 + z - 1 2 = y + 1 2

x 2 + z - 1 2 = 2 y + 1

x 2 2 + z - 1 2 2 = y + 1 2

Que é a equação do paraboloide Elíptico

Resposta

Parabolóide Elíptico com equação:

x 2 2 + z - 1 2 2 = y + 1 2

P = ( x , y , z )

Exercício Resolvido #4

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2004, pp. 68 - 6.

Considere a quádrica a seguir:

x 2 + 5 y 2 = 8 z 2

Identifique a quádrica, encontre os traços, determine as seções e esboce seu gráfico.

Passo 1

Podemos ajeitar a equação da quádrica para ficar na seguinte forma:

x 2 40 + y 2 8 = z 2 5

Que é a equação do cone elíptico.

Passo 2

Vamos agora determinar os traços:

  • Plano x y   ( z = 0 ) :

    • x 2 40 + y 2 8 = 0

    É o ponto 0 , 0,0

  • Plano y z   ( x = 0 ) :

    • y 2 8 = z 2 5

    z = ± 5 8 y

    Temos um par de retas.

  • Plano x z   ( y = 0 ) :

x 2 40 = z 2 5

z = ± 1 8 x

Também temos um par de retas.

Passo 3

Vamos determinar seções paralelas aos planos coordenados.

Interseções:

  • Plano z = k

    • x 2 40 + y 2 8 = k 2 5

    Se k ≠ 0 :

    x 2 40 ( k 2 5 ) + y 2 8 ( k 2 5 ) = 1

    São elipses para k ∈ R   ,   k   ≠ 0

  • Plano y = k

    • x 2 40 + k 2 8 = z 2 5 → x 2 40 - z 2 5 = - k 2 8

    Se k ≠ 0

    x 2 40 ( - k 2 8 ) - z 2 5 ( - k 2 8 ) = 1

    São Hipérboles para k ∈ R   ,   k   ≠ 0

  • Plano x = k

k 2 40 + y 2 8 = z 2 5 → y 2 8 - z 2 5 = - k 2 40

Se k ≠ 0 :

y 2 8 ( - k 2 40 ) - z 2 5 ( - k 2 40 ) = 1

São Hipérboles para k ∈ R   ,   k   ≠ 0

Passo 4

Primeiramente desenhe os traços que a gente achou. Após isso, perceba que as interseções com planos paralelos ao eixo z são elipses. Logo,para representar isso, desenhe duas elipses: uma no topo e outra na parte inferior. O gráfico fica:

Resposta

A quádrica é um cone elíptico . Ela tem os seguintes traços: o ponto ( 0,0 , 0 ) no plano x y , retas z = ± 5 8 y no plano y z e retas z = ± 1 8 x no plano x z .

As interseções com planos k paralelos aos eixos coordenados , com k ≠ 0 , são: No plano z = k temos elipses, e nos plnos x = k e y = k temos hipérboles.

O gráfico fica:

Exercício Resolvido #5

Georg B. Thomas, Cálculo Volume 2, 11ª ed. São Paulo: PEARSON, 2008, pp. 218 - 65

Esboce o gráfico da quádrica a seguir:

z = - ( x 2 + y 2 )

Passo 1

A quádrica apresentada no enunciado é um paraboloide elíptico, pois do lado esquerdo da equação tem uma variável “isolada” de grau 1 e do lado direito tem variáveis de grau 2 com sinais iguais.

Passo 2

Vamos fazer os traços:

Traços:

  • Traço no plano x y   z = 0 :

    • 0 = - ( x 2 + y 2 )

    Temos o ponto ( 0,0 , 0 )

  • Traço no plano x z   ( y = 0 ) :

    • z = - x 2

    Temos uma parábola. O traço fica:

  • Traço no plano y z   ( x = 0 ) :

    • z = - y 2

    Temos uma parábola. O traço fica:

    Passo 4

    Vamos fazer agora interseções com planos paralelos aos eixos coordenados.

    Interseções:

  • Plano z = k

    • k = - ( x 2 + y 2 )

    Se k = 0 temos o ponto 0,0 , 0

    Se k ≠ 0 temos:

    1 = - x 2 + y 2 k

    Se k > 0 a equação acima é impossível. Logo não há interseção.

    Se k < 0 então a equação acima é um círculo.

    São elipses para k < 0

  • Plano y = k

    • z = - ( x 2 + k 2 )

    São Parábolas para k ∈ R  

  • Plano x = k

z = - ( k 2 + y 2 )

São Parábolas para k ∈ R  

Passo 3

Plote os traços que encontramos. Como as interseções da quádrica com eixos paralelos ao eixo z são elipses, para k < 0 , desenhe uma elipse na parte mais negativa do eixo z para demonstrar isso. O esboço fica:

Resposta

Exercício Resolvido #6

Elaboração própria

Identifique as superfícies quadráticas abaixo e esboce seu gráfico.

S 1 : z = 4 - 2 x 2 - 3 y 2

S 2 : z = 4 - 2 x 2 + 3 y 2

Passo 1

Antes de tentar identificar a Quádrica devemos completar os quadrados na equação, vamos começar pela S 1 marotamente porque não precisa completar o quadrado. Porque não precisa? Ele só tem caras ao quadrado ou z sem estar elevado a ninguém. Se tivesse alguém ao quadrado e essa mesma letra não elevada ao quadrado ai sim iríamos completar quadrados.

Temos

z = 4 - 2 x 2 - 3 y 2

z - 4 = - 2 x 2 - 3 y 2

Como temos z sem estar ao quadrado e x e y tem o mesmo sinal temos um paraboloide elíptico. Mas como não temos o z sozinho ele está deslocado, fica atento a isso.

Ele vai ter a “Pontinha” no ponto 0,0 , 4

O gráfico vai ficar

Passo 2

A superfície S 2 também não precisa completar quadrado, fica muito atento que agora temos uma equação onde os sinais dos caras ao quadrado são diferente, isso nos diz que isso é um paraboloide hiperbólico, vulgo sela.

z = 4 - 2 x 2 + 3 y 2

z - 4 = - 2 x 2 + 3 y 2

O gráfico vai ficar

Repara que o eixo da sela está na direção do eixo y , só que deslocado para cima, ou seja, com z = 4 , que é o que aquele 4 está fazendo.

Resposta

Exercício Resolvido #7

Elaboração própria

Identifique essa Quádrica e faça seu esboço

- x 2 + y 2 + z 2 - 2 x - 2 z = 0

Passo 1

Vamos fazer a superfície S 1

Temos em x

- x 2 - 2 x - b 2 = - a 2 - 2 a b - b 2

Porque coloquei tudo negativo dessa vez? O x 2 está negativo, então agora temos que por todo mundo negativo, se ele for positivo é como antes, sacou?

Então

- a 2 = - x 2 ⟹ a = x

- 2 x = - 2 a b ⟹ - 2 x = - 2 b x ⟹ b = 1

Dessa forma devemos somar dos dois lados - b 2 = - 1

Vamos ter em y do lado esquerdo

- x 2 - 2 x - 1

Está lindão essa porra né? Só que não. O ideal é sempre termos a letra multiplicando 1 então vamos por - 1 em evidência

- 1 x 2 + 2 x + 1 = - x + 1 2

Beleza?

Passo 2

Vamos para z agora

z 2 - 2 z + b 2 = a 2 + 2 a b + b 2

Então

a 2 = z 2 ⟹ a = z

- 2 z = 2 a b ⟹ - 2 z = 2 z b ⟹ b = 1

Dessa forma devemos somar dos dois lados b 2 = 1

Vamos ter em y do lado esquerdo

z 2 - 2 z + 1 = z - 1 2

Beleza?

Passo 3

A equação vai ficar

- x + 1 2 + y 2 + z - 1 2 = - 1 + 1 = 0

- x + 1 2 + y 2 + z - 1 2 = 0

y 2 + z - 1 2 = x + 1 2

Essa é uma equação de um cone, com eixo igual ao eixo x , mas a ponta do coné não vai ser na origem vai ser no ponto - 1,0 , 1

O gráfico vai ficar

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #8

UFRJ - Cálculo 2 - P1 2012.2 – 4a

z = x 2 + y 2

Faça um esboço da superfície, destacando as curvas de interseção com os planos coordenados x = 0 , y = 0 e z = 0 .

Passo 1

Identificar a superfície:

z = x 2 + y 2

⇒ z 2 = x 2 + y 2

Essa é a equação de um cone circular.

Mas como z = x 2 + y 2 > 0 , então o gráfico dessa superfície é apenas a parte superior do cone:

x = 0 → z = y 2 = y → Retas

y = 0 → z = x 2 = x → Retas

z = 0 → x 2 + y 2 = 0 ⇒ x = y = 0 → Ponto

Resposta

Exercícios de Livros Relacionados

Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
Os Exercícios 45-48 fornecem equações para parábolas e nos dize quantas unidades para cima ou para baixo e para direita ou para esquerda cada parábola deve ser deslocada. Encontre uma equação para a n
A parábola y2 = 8x é deslocada 2 unidades para baixo e 1 unidade para a direita para gerar a parábola (y + 2)2 = 8(x - 1). a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente grafica
A parábola X2 = -4y é deslocada 1 unidades para esquerda e 3 unidade para cima para gerar a parábola (x+1)=4(y-3) a. Encontre o vértice, foco e diretriz da nova parábola.b. Represente graficamente os