Formas Quadráticas – Cônicas
Produzido por Mariana PessanhaTeoria
Introdução
Fala, galera! Tudo bem? Hoje nós vamos continuar estudando as famosas cônicas. Porém agora de uma maneira um pouquinho diferente do que a gente está acostumado.
Antes de mais nada, vamos relembrar as equações das cônicas que já estudamos:
- Elipse:
- Hipérbole:
- Parábola:
- Os termos lineares de e (ex: e ) indicam que essa cônica está deslocada em relação à origem, ou seja, seu centro NÃO é o ponto (0;0) do plano cartesiano.
- Os termos da equação indicam que ela está rotacionada, ou seja, os eixos de simetria da cônica NÃO são paralelos aos eixos e do plano cartesiano.
Se temos uma circunferência.
Qualquer dúvida volte na parte de “seções cônicas”.
Beleza! Agora considere a seguinte equação:
A princípio ela não se encaixa em nenhuma das cônicas que vimos. Mas e se eu te disser que essa equação é sim uma cônica???

WTF!!
CALMA, CALMA, NADA DE PÂNICO! Ela é uma cônica, porém está rotacionada e deslocada da origem.
Vamos ver, a seguir, tudo que você precisa saber sobre esse assunto. Não se preocupe. Nós iremos com calma, passo a passo e você vai ver que não é tão complicado quanto parece.
Representação Matricial:
Como já dito, vimos basicamente 3 tipos de equações de cônicas. Mas na verdade, cônica é o conjunto dos pontos que satisfazem a equação:
Onde não são todos nulos.
Voltando ao exemplo incial, reparem que a equação:
É uma cônica e que pode ser reescrita na forma matricial:
Veja que ambas as expressões são equivalentes. Fazendo a multiplicação matricial temos:
Portanto, quando você tiver uma equação assim, você pode reescrevê-la na forma matricial, da seguinte maneira:
E quando reescrevemos na forma matricial, aparece ali uma matriz que vai ser fundamental pro nosso desenvolvimento!!
Essa matriz associada à cônica é simétrica e diagonalizável!!!! Isso significa que podemos escrevê-la em função de seus autovalores e autovetores. E é isso que nós precisamos pra fazer nossa contas!
Cônicas Rotacionadas
Bom, vamos voltar a equação na forma incial:
Os termos quadráticos de e indicam que essa equação é de uma forma quadrática, mesmo nome lá do título. Isso quer dizer, essencialmente, que estamos trabalhando com cônicas no caso de só ter e na equação, ou quádricas no caso de ter e , que veremos em outro capítulo mais pra frente (não se preocupe com isso agora).
Então, vamos falar das cônicas. Temos duas observações muito importantes:
Como nossa cônica está rotacionada e com o centro fora da origem, nós temos que encontrar os eixose nos quais a cônica está certinha. Olha só:
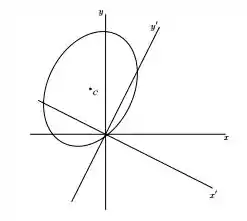
Tinhamos a equação de uma cônica qualquer da forma:
Reescrevemos ela na forma matricial:
Para encontrar os eixos e , vamos reescrever a equação da cônica utilizando os autovalores e autovetores da matriz .
A equação deverá ficar assim:
Aonde e são os mesmos da equação geral que vimos ali em cima, e e são os eixos nos quais a cônica está.
Reparem que na equação acima, e são os autovalores da matriz . E os vetores ) e são os autovetores UNITÁRIOS associados a e , respectivamente! Ou seja, a disposição dos autovetores na matriz deve acompanhar a dos autovalores.
Só pra relembrar, pra achar o UNITÁRIO de um vetor, basta dividir as coordenadas do vetor pelo seu MÓDULO!!!
Então, resumindo:
Pra reescrever as equações “estranhas” de uma forma que nós saibamos dizer com qual cônica estamos tratando, devemos primeiro escrever a equação na forma matricial, pra identificarmos a matriz .
Feito isso, calculamos seus autovalores e e autovetores associados unitários ) e pra depois podermos reescrever a equação da seguinte forma:
Depois de reescrita, é só multiplicar as matrizes e pronto! Tá aí o que a gente queria!!!
Exemplo Completo
Vamos ver um exemplo disso, pro caso daquele exemplo lá do início:
- Escrevemos na forma matricial:
- Agora temos que encontrar os autovalores de .
- Agora, temos de encontrar os autovetores unitários.
Bom, para encontrar os autovalores de uma matriz 2x2 fazemos o seguinte:
Precisamos fazer:
Isso implica :
Montamos um polinômio característico e resolvemos. Os valores encontrados vão ser os autovalores. Vou mostrar:
No caso, a nossa matriz é:
O polinômio característico vai ser:
Resolvendo essa equação, achamos os autovalores de , que são e
Para uma matriz 2x2:
Com autovalores e vamos encontrar autovetores associados a cada autovalor.
Autovetor associado a :
Onde é um vetor qualquer com coordenadas:
A expressão matricial fica:
Fazendo a multiplicação matricial temos o seguinte sistema:
Autovetor associado a :
Onde é um vetor qualquer com coordenadas:
A expressão matricial fica:
Fazendo a multiplicação matricial temos o seguinte sistema:
Aplicando ao nosso exemplo:
- Autovetor associado a :
- Autovetor associado a :
Onde , obedecem a seguinte equação:
Encontramos:
Portanto
Arbitrando um valor qualquer para , por exemplo temos:
Porém necessitamos do autovetor unitário. Fazemos então:
Onde , obedecem a seguinte equação:
Encontramos então:
Portanto
Arbitrando valor para , por exemplo temos:
Porém necessitamos do autovetor unitário. Fazemos então:
E multiplicando as matrizes, chegamos em:
Agora o que temos é a equação da cônica nos eixos e .
Se você não lembra como completar quadrados, vamos revisar rapidamente:
A ideia é pegar a equação que tem termos quadráticos e lineares de e , e reescrevê-la com os termos e . Para isso, devemos primeiramente colocar em evidência o coeficiente do termo quadrático Feito isso, pegamos o coeficiente do termo linear, dividimos por , elevamos ao quadrado e somamos o resultado dos lados da equação. UFA! Vamos ver um exemplo pra ficar mais claro:
Então colocando em evidência, teremos:
Agora, com os coeficientes dos termos lineares, dividimos por 2 e elevamos ao quadrado. Veja só:
E finalmente, somamos esses termos que encontramos em ambos os lados da equação. Porém, repare que devemos somar os termos dentro dos parênteses, como objetivo de criar um Trinômio Quadrado Perfeito pra podermos escrever como e
E como somamos dentro dos parênteses, temos que somar do outro lado da equação os valores multiplicados pelo que está em evidência!!!!
Finalmente, podemos escrever:
E então a equação vai ficar:
Pra identificarmos melhor a cônica, dividimos a equação toda por , pra equação ficar igualada a . E até que enfim:
ALELUIA, ALELUIA, CHEGAMOS A UMA EQUAÇÃO CONHECIDA!!!! UUUUUFA!
Agora sim, vemos que a equação lá do início é uma elipse, centrada em , e com semieixos nas direções e iguais a e , respectivamente.
Observação:
Lembra que nossos eixos e estão rotacionados em relação a e ?? Legal, muito bonito, mas aonde estão esses eixos? Que eixos são esses?? E se me pedirem pra desenhar a cônica nos eixos e ?? RELAXA, É SIMPLES!
Os eixos são dados pelos autovetores que a gente achou lá da matriz , lembra?? Pois é, então é só desenhar a direção daqueles autovetores:
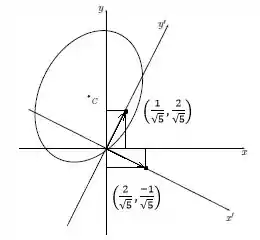
Cônicas Degeneradas:
Essa é a última parte da teoria. Lá no início da teoria eu disse que cônicas são todas as equações do tipo:
Beleza! Então vamos ver um exemplo:
Ela satisfaz a equação de uma quádrica, portanto ela é uma quádrica. Vamos arrumar essa equação. Ajeitando os quadrados temos:
Pera!!! Mas isso não é uma elipse, hipérbole ou parábola. Isso representa um ponto. Veja que a soma de coisas ao quadrado só será 0 se ambas as parcelas forem 0. Então a equação é a equação do ponto .
Exatamente! Quando a equação está na forma , ela é uma cônica. Porém quando essa cônica não é uma elipse/circunferência, hipérbole ou parábola, dizemos que ela é uma Cônica Degenerada.
As cônicas degeneradas podem representar um par de retas, uma só reta, um ponto ou um conjunto vazio.