Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 63

Ache o volume do sólido gerado pela rotação, em torno do eixo y, da região limitada pela hiperbole x 2 / a 2 - y 2 / b 2 = 1 e pela reta x = 2 a

Passo 1

Primeiro vamos fazer um esboço da região. Como a rotação é em torno do eixo y, precisaremos encontrar duas funções x = f ( y ) que delimitem a região que será rotacionada. A reta já é uma função dada nesse formato, precisaremos encontrar uma função assim para a hiperbole isolando o termo x:

x 2 a 2 - y 2 b 2 = 1

x 2 a 2 = 1 + y 2 b 2

x 2 = a 2 1 + y 2 b 2

x = a 2 1 + y 2 b 2             ( 1 )

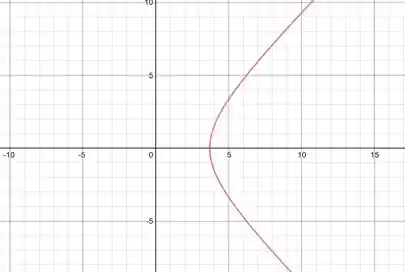
Passo 2

O que falta é apenas encontrar os pontos de intersecção entre a hipérbole da equação (1) e a reta x = 2 a . Vamos fazer o sistema:

x = 2 a x = a 2 1 + y 2 b 2   ⟹   2 a = a 2 1 + y 2 b 2

4 a 2 = a 2 1 + y 2 b 2

4 = 1 + y 2 b 2

y 2 = 3 b 3

y = ± 3 b

Encontrado o ponto y, sabemos que os pontos de intersecção são os pontos ( 2 a , 3 b ) e ( 2 a , - 3 b ) .

Passo 3

Agora que conseguimos definir uma região delimitada por duas funções de y , é possível calcular o volume do sólido gerado por sua rotação em torno do próprio eixo y utilizando a fórmula:

V = π ∫ c d f y 2 - g x 2   d y

V = π ∫ - 3 b 3 b 2 a 2 - a 2 1 + y 2 b 2 2 d y

V = 2 π ∫ 0 3 b 4 a 2 - a 2 1 + y 2 b 2 d y

V = 2 π a 2 ∫ 0 3 b 4 - 1 + y 2 b 2   d y

V = 2 π a 2 ∫ 0 3 b 3 + y 2 b 2   d y

V = 2 π a 2 3 y + y 3 3 b 2 0 3 b = 2 π a 2 3 3 b + b 3 3 3 3 b 2

V = 2 π a 2 3 3 b + 3 b = 2 π a 2 2 3 b

V = 4 3 π a 2 b

Resposta

V = 4 3 π a 2 b

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a curva r = 2 ( 1 + s e n θ ) , ache X e α no ponto (1, 2 3 π ) . Faça um esboço da curva mostrando X e α .
Para a curva r = 2 cos ⁡ 1 2 θ ache X e α no ponto (1, 1 6 π ) . Faça um esboço da curva mostrando X e α .
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com
Nos exercícios de 13 a 20, coloque num gráfico o ponto com coordenadas polares dadas; dê, então, dois outros conjuntos de coordenadas polares para o mesmo ponto; um com o mesmo valor de r e outro com